Vector Copula Variational Inference and Dependent Block Posterior Approximations

Variational inference (VI) is a popular method to estimate statistical and econometric models. The key to VI is the selection of a tractable density to approximate the Bayesian posterior. For large and complex models a common choice is to assume independence between multivariate blocks in a partition of the parameter space. While this simplifies the problem it can reduce accuracy. This paper proposes using vector copulas to capture dependence between the blocks parsimoniously. Tailored multivariate marginals are constructed using learnable cyclically monotone transformations. We call the resulting joint distribution a ``dependent block posterior'' approximation. Vector copula models are suggested that make tractable and flexible variational approximations. They allow for differing marginals, numbers of blocks, block sizes and forms of between block dependence. They also allow for solution of the variational optimization using fast and efficient stochastic gradient methods. The efficacy and versatility of the approach is demonstrated using four different statistical models and 16 datasets which have posteriors that are challenging to approximate. In all cases, our method produces more accurate posterior approximations than benchmark VI methods that either assume block independence or factor-based dependence, at limited additional computational cost.

Optimal reconciliation with immutable forecasts

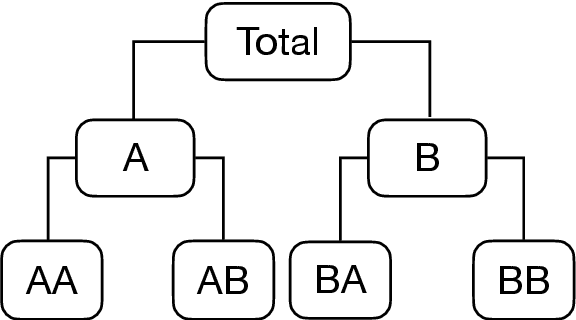
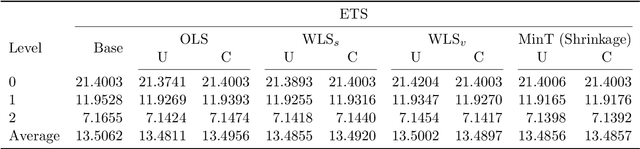
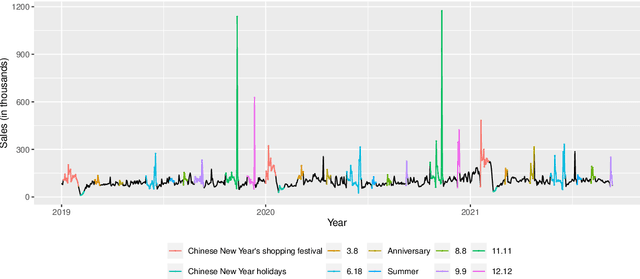
The practical importance of coherent forecasts in hierarchical forecasting has inspired many studies on forecast reconciliation. Under this approach, so-called base forecasts are produced for every series in the hierarchy and are subsequently adjusted to be coherent in a second reconciliation step. Reconciliation methods have been shown to improve forecast accuracy, but will, in general, adjust the base forecast of every series. However, in an operational context, it is sometimes necessary or beneficial to keep forecasts of some variables unchanged after forecast reconciliation. In this paper, we formulate reconciliation methodology that keeps forecasts of a pre-specified subset of variables unchanged or "immutable". In contrast to existing approaches, these immutable forecasts need not all come from the same level of a hierarchy, and our method can also be applied to grouped hierarchies. We prove that our approach preserves unbiasedness in base forecasts. Our method can also account for correlations between base forecasting errors and ensure non-negativity of forecasts. We also perform empirical experiments, including an application to sales of a large scale online retailer, to assess the impacts of our proposed methodology.

Updating Variational Bayes: Fast sequential posterior inference

Variational Bayesian (VB) methods produce posterior inference in a time frame considerably smaller than traditional Markov Chain Monte Carlo approaches. Although the VB posterior is an approximation, it has been shown to produce good parameter estimates and predicted values when a rich classes of approximating distributions are considered. In this paper we propose Updating VB (UVB), a recursive algorithm used to update a sequence of VB posterior approximations in an online setting, with the computation of each posterior update requiring only the data observed since the previous update. An extension to the proposed algorithm, named UVB-IS, allows the user to trade accuracy for a substantial increase in computational speed through the use of importance sampling. The two methods and their properties are detailed in two separate simulation studies. Two empirical illustrations of the proposed UVB methods are provided, including one where a Dirichlet Process Mixture model with a novel posterior dependence structure is repeatedly updated in the context of predicting the future behaviour of vehicles on a stretch of the US Highway 101.