Natural Gradient Hybrid Variational Inference with Application to Deep Mixed Models

Stochastic models with global parameters $\bm{\theta}$ and latent variables $\bm{z}$ are common, and variational inference (VI) is popular for their estimation. This paper uses a variational approximation (VA) that comprises a Gaussian with factor covariance matrix for the marginal of $\bm{\theta}$, and the exact conditional posterior of $\bm{z}|\bm{\theta}$. Stochastic optimization for learning the VA only requires generation of $\bm{z}$ from its conditional posterior, while $\bm{\theta}$ is updated using the natural gradient, producing a hybrid VI method. We show that this is a well-defined natural gradient optimization algorithm for the joint posterior of $(\bm{z},\bm{\theta})$. Fast to compute expressions for the Tikhonov damped Fisher information matrix required to compute a stable natural gradient update are derived. We use the approach to estimate probabilistic Bayesian neural networks with random output layer coefficients to allow for heterogeneity. Simulations show that using the natural gradient is more efficient than using the ordinary gradient, and that the approach is faster and more accurate than two leading benchmark natural gradient VI methods. In a financial application we show that accounting for industry level heterogeneity using the deep model improves the accuracy of probabilistic prediction of asset pricing models.

Bayesian Neural Network Versus Ex-Post Calibration For Prediction Uncertainty

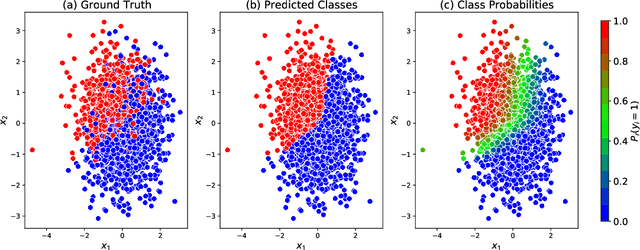
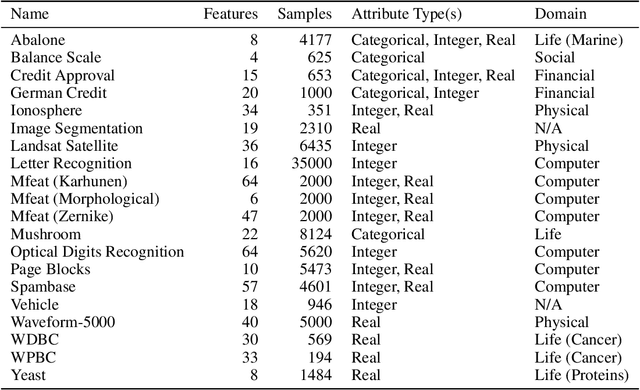
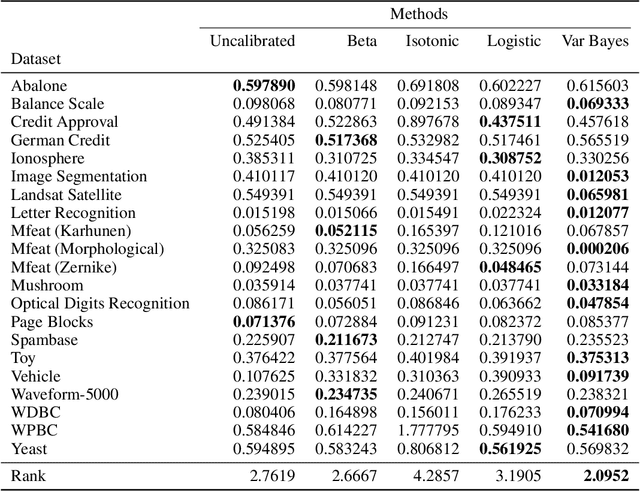
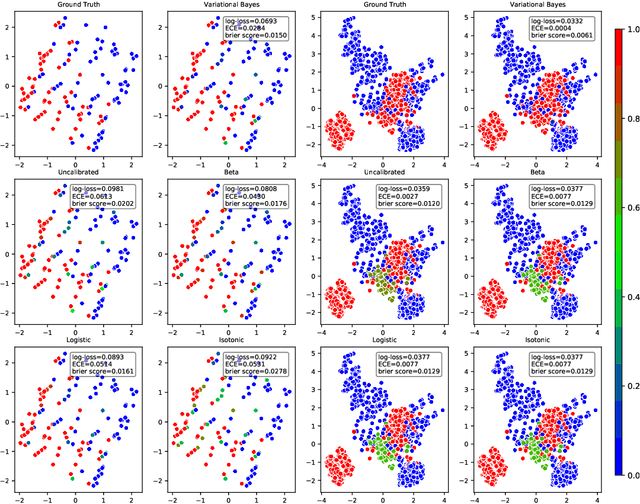
Probabilistic predictions from neural networks which account for predictive uncertainty during classification is crucial in many real-world and high-impact decision making settings. However, in practice most datasets are trained on non-probabilistic neural networks which by default do not capture this inherent uncertainty. This well-known problem has led to the development of post-hoc calibration procedures, such as Platt scaling (logistic), isotonic and beta calibration, which transforms the scores into well calibrated empirical probabilities. A plausible alternative to the calibration approach is to use Bayesian neural networks, which directly models a predictive distribution. Although they have been applied to images and text datasets, they have seen limited adoption in the tabular and small data regime. In this paper, we demonstrate that Bayesian neural networks yields competitive performance when compared to calibrated neural networks and conduct experiments across a wide array of datasets.

Variational Bayes Estimation of Discrete-Margined Copula Models with Application to Time Series

We propose a new variational Bayes estimator for high-dimensional copulas with discrete, or a combination of discrete and continuous, margins. The method is based on a variational approximation to a tractable augmented posterior, and is faster than previous likelihood-based approaches. We use it to estimate drawable vine copulas for univariate and multivariate Markov ordinal and mixed time series. These have dimension $rT$, where $T$ is the number of observations and $r$ is the number of series, and are difficult to estimate using previous methods. The vine pair-copulas are carefully selected to allow for heteroskedasticity, which is a feature of most ordinal time series data. When combined with flexible margins, the resulting time series models also allow for other common features of ordinal data, such as zero inflation, multiple modes and under- or over-dispersion. Using six example series, we illustrate both the flexibility of the time series copula models, and the efficacy of the variational Bayes estimator for copulas of up to 792 dimensions and 60 parameters. This far exceeds the size and complexity of copula models for discrete data that can be estimated using previous methods.