Bayesian Neural Network Versus Ex-Post Calibration For Prediction Uncertainty

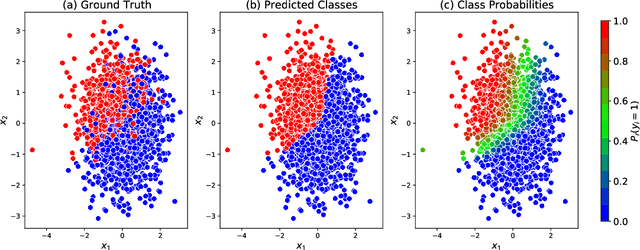
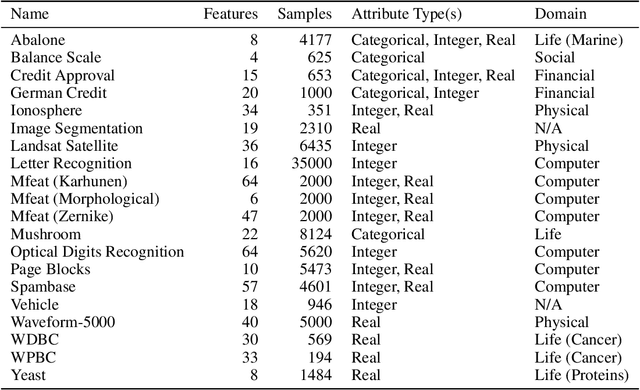
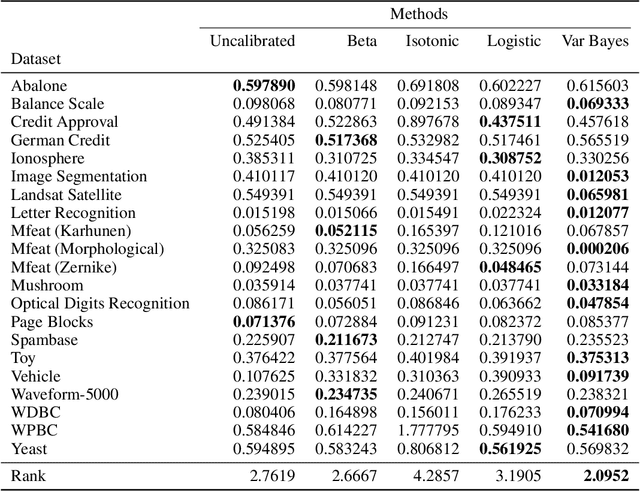
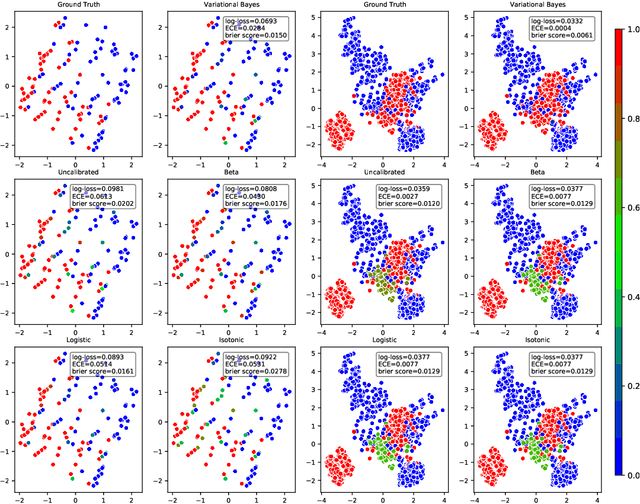
Probabilistic predictions from neural networks which account for predictive uncertainty during classification is crucial in many real-world and high-impact decision making settings. However, in practice most datasets are trained on non-probabilistic neural networks which by default do not capture this inherent uncertainty. This well-known problem has led to the development of post-hoc calibration procedures, such as Platt scaling (logistic), isotonic and beta calibration, which transforms the scores into well calibrated empirical probabilities. A plausible alternative to the calibration approach is to use Bayesian neural networks, which directly models a predictive distribution. Although they have been applied to images and text datasets, they have seen limited adoption in the tabular and small data regime. In this paper, we demonstrate that Bayesian neural networks yields competitive performance when compared to calibrated neural networks and conduct experiments across a wide array of datasets.

Creating Powerful and Interpretable Models withRegression Networks

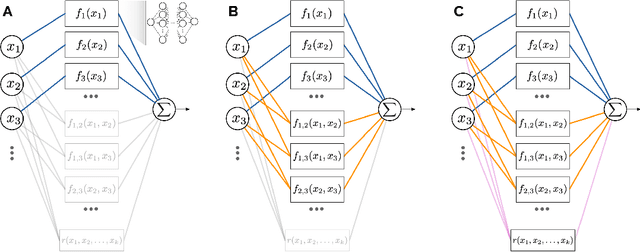
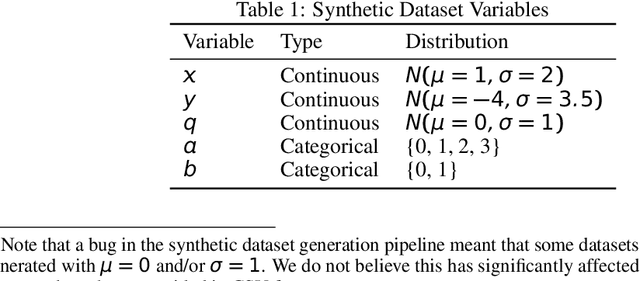
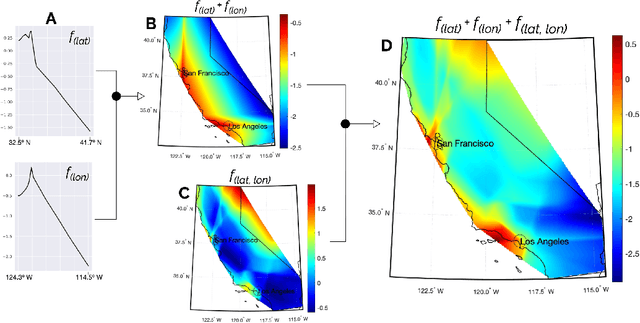
As the discipline has evolved, research in machine learning has been focused more and more on creating more powerful neural networks, without regard for the interpretability of these networks. Such "black-box models" yield state-of-the-art results, but we cannot understand why they make a particular decision or prediction. Sometimes this is acceptable, but often it is not. We propose a novel architecture, Regression Networks, which combines the power of neural networks with the understandability of regression analysis. While some methods for combining these exist in the literature, our architecture generalizes these approaches by taking interactions into account, offering the power of a dense neural network without forsaking interpretability. We demonstrate that the models exceed the state-of-the-art performance of interpretable models on several benchmark datasets, matching the power of a dense neural network. Finally, we discuss how these techniques can be generalized to other neural architectures, such as convolutional and recurrent neural networks.