Creating Powerful and Interpretable Models withRegression Networks

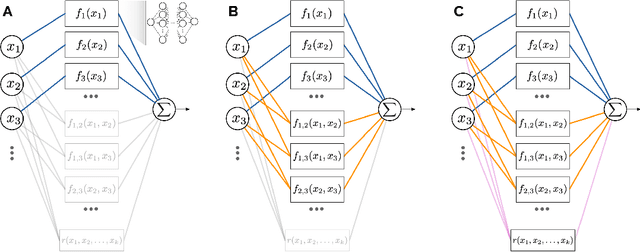
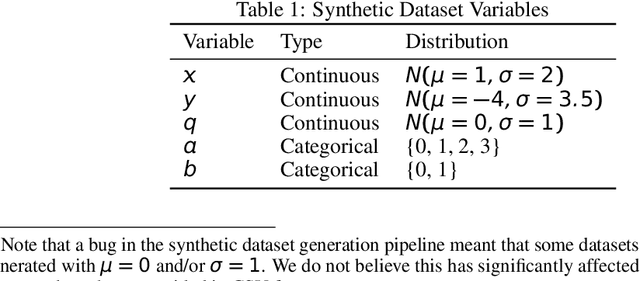
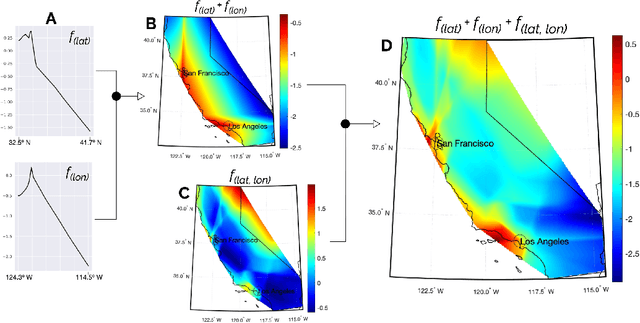
As the discipline has evolved, research in machine learning has been focused more and more on creating more powerful neural networks, without regard for the interpretability of these networks. Such "black-box models" yield state-of-the-art results, but we cannot understand why they make a particular decision or prediction. Sometimes this is acceptable, but often it is not. We propose a novel architecture, Regression Networks, which combines the power of neural networks with the understandability of regression analysis. While some methods for combining these exist in the literature, our architecture generalizes these approaches by taking interactions into account, offering the power of a dense neural network without forsaking interpretability. We demonstrate that the models exceed the state-of-the-art performance of interpretable models on several benchmark datasets, matching the power of a dense neural network. Finally, we discuss how these techniques can be generalized to other neural architectures, such as convolutional and recurrent neural networks.

The IMP game: Learnability, approximability and adversarial learning beyond $Σ^0_1$

We introduce a problem set-up we call the Iterated Matching Pennies (IMP) game and show that it is a powerful framework for the study of three problems: adversarial learnability, conventional (i.e., non-adversarial) learnability and approximability. Using it, we are able to derive the following theorems. (1) It is possible to learn by example all of $\Sigma^0_1 \cup \Pi^0_1$ as well as some supersets; (2) in adversarial learning (which we describe as a pursuit-evasion game), the pursuer has a winning strategy (in other words, $\Sigma^0_1$ can be learned adversarially, but $\Pi^0_1$ not); (3) some languages in $\Pi^0_1$ cannot be approximated by any language in $\Sigma^0_1$. We show corresponding results also for $\Sigma^0_i$ and $\Pi^0_i$ for arbitrary $i$.

On the universality of cognitive tests

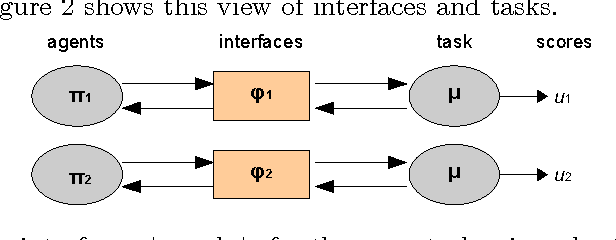
The analysis of the adaptive behaviour of many different kinds of systems such as humans, animals and machines, requires more general ways of assessing their cognitive abilities. This need is strengthened by increasingly more tasks being analysed for and completed by a wider diversity of systems, including swarms and hybrids. The notion of universal test has recently emerged in the context of machine intelligence evaluation as a way to define and use the same cognitive test for a variety of systems, using some principled tasks and adapting the interface to each particular subject. However, how far can universal tests be taken? This paper analyses this question in terms of subjects, environments, space-time resolution, rewards and interfaces. This leads to a number of findings, insights and caveats, according to several levels where universal tests may be progressively more difficult to conceive, implement and administer. One of the most significant contributions is given by the realisation that more universal tests are defined as maximisations of less universal tests for a variety of configurations. This means that universal tests must be necessarily adaptive.