Semantically enriched spatial modelling of industrial indoor environments enabling location-based services

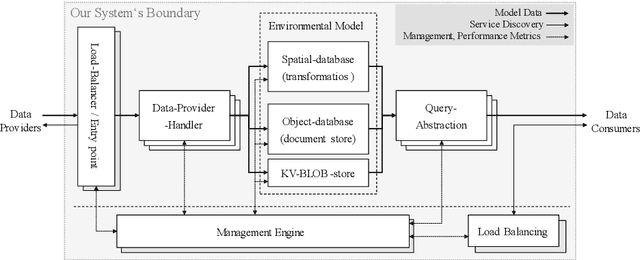
This paper presents a concept for a software system called RAIL representing industrial indoor environments in a dynamic spatial model, aimed at easing development and provision of location-based services. RAIL integrates data from different sensor modalities and additional contextual information through a unified interface. Approaches to environmental modelling from other domains are reviewed and analyzed for their suitability regarding the requirements for our target domains; intralogistics and production. Subsequently a novel way of modelling data representing indoor space, and an architecture for the software system are proposed.

Risk-averse estimation, an axiomatic approach to inference, and Wallace-Freeman without MML

We define a new class of Bayesian point estimators, which we refer to as risk-averse estimators. We then use this definition to formulate several axioms that we claim to be natural requirements for good inference procedures, and show that for two classes of estimation problems the axioms uniquely characterise an estimator. Namely, for estimation problems with a discrete hypothesis space, we show that the axioms lead to the MAP estimate, whereas for well-behaved, purely continuous estimation problems the axioms lead to the Wallace-Freeman estimate. Interestingly, this combined use of MAP and Wallace-Freeman estimation reflects the common practice in the Minimum Message Length (MML) community, but there these two estimators are used as approximations for the information-theoretic Strict MML estimator, whereas we derive them exactly, not as approximations, and do so with no use of encoding or information theory.

RKL: a general, invariant Bayes solution for Neyman-Scott

Neyman-Scott is a classic example of an estimation problem with a partially-consistent posterior, for which standard estimation methods tend to produce inconsistent results. Past attempts to create consistent estimators for Neyman-Scott have led to ad-hoc solutions, to estimators that do not satisfy representation invariance, to restrictions over the choice of prior and more. We present a simple construction for a general-purpose Bayes estimator, invariant to representation, which satisfies consistency on Neyman-Scott over any non-degenerate prior. We argue that the good attributes of the estimator are due to its intrinsic properties, and generalise beyond Neyman-Scott as well.

MML is not consistent for Neyman-Scott

Strict Minimum Message Length (SMML) is a statistical inference method widely cited (but only with informal arguments) as providing estimations that are consistent for general estimation problems. It is, however, almost invariably intractable to compute, for which reason only approximations of it (known as MML algorithms) are ever used in practice. We investigate the Neyman-Scott estimation problem, an oft-cited showcase for the consistency of MML, and show that even with a natural choice of prior, neither SMML nor its popular approximations are consistent for it, thereby providing a counterexample to the general claim. This is the first known explicit construction of an SMML solution for a natural, high-dimensional problem. We use the same novel construction methods to refute other claims regarding MML also appearing in the literature.

The IMP game: Learnability, approximability and adversarial learning beyond $Σ^0_1$

We introduce a problem set-up we call the Iterated Matching Pennies (IMP) game and show that it is a powerful framework for the study of three problems: adversarial learnability, conventional (i.e., non-adversarial) learnability and approximability. Using it, we are able to derive the following theorems. (1) It is possible to learn by example all of $\Sigma^0_1 \cup \Pi^0_1$ as well as some supersets; (2) in adversarial learning (which we describe as a pursuit-evasion game), the pursuer has a winning strategy (in other words, $\Sigma^0_1$ can be learned adversarially, but $\Pi^0_1$ not); (3) some languages in $\Pi^0_1$ cannot be approximated by any language in $\Sigma^0_1$. We show corresponding results also for $\Sigma^0_i$ and $\Pi^0_i$ for arbitrary $i$.