On a Variational Approximation based Empirical Likelihood ABC Method

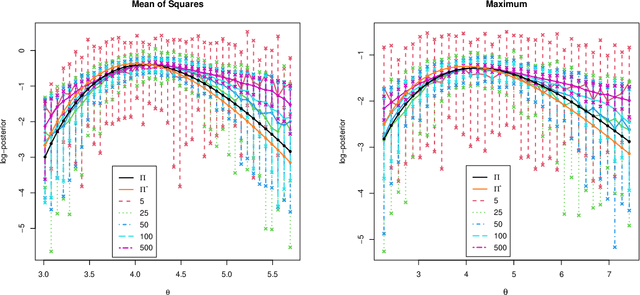
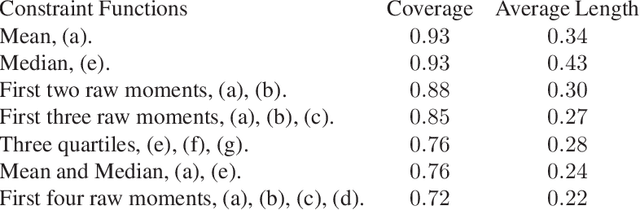
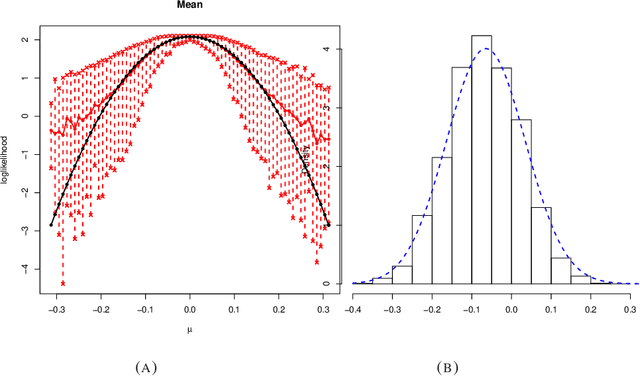
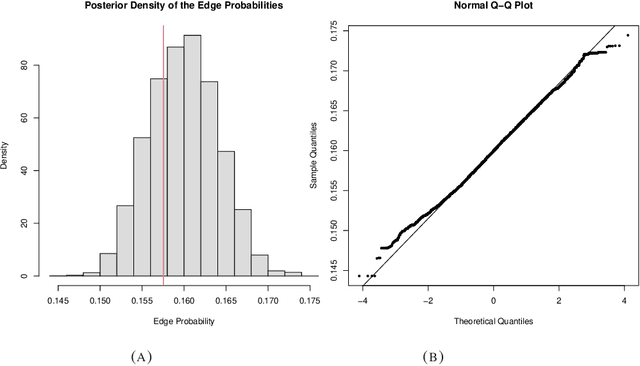
Many scientifically well-motivated statistical models in natural, engineering, and environmental sciences are specified through a generative process. However, in some cases, it may not be possible to write down the likelihood for these models analytically. Approximate Bayesian computation (ABC) methods allow Bayesian inference in such situations. The procedures are nonetheless typically computationally intensive. Recently, computationally attractive empirical likelihood-based ABC methods have been suggested in the literature. All of these methods rely on the availability of several suitable analytically tractable estimating equations, and this is sometimes problematic. We propose an easy-to-use empirical likelihood ABC method in this article. First, by using a variational approximation argument as a motivation, we show that the target log-posterior can be approximated as a sum of an expected joint log-likelihood and the differential entropy of the data generating density. The expected log-likelihood is then estimated by an empirical likelihood where the only inputs required are a choice of summary statistic, it's observed value, and the ability to simulate the chosen summary statistics for any parameter value under the model. The differential entropy is estimated from the simulated summaries using traditional methods. Posterior consistency is established for the method, and we discuss the bounds for the required number of simulated summaries in detail. The performance of the proposed method is explored in various examples.

An easy-to-use empirical likelihood ABC method

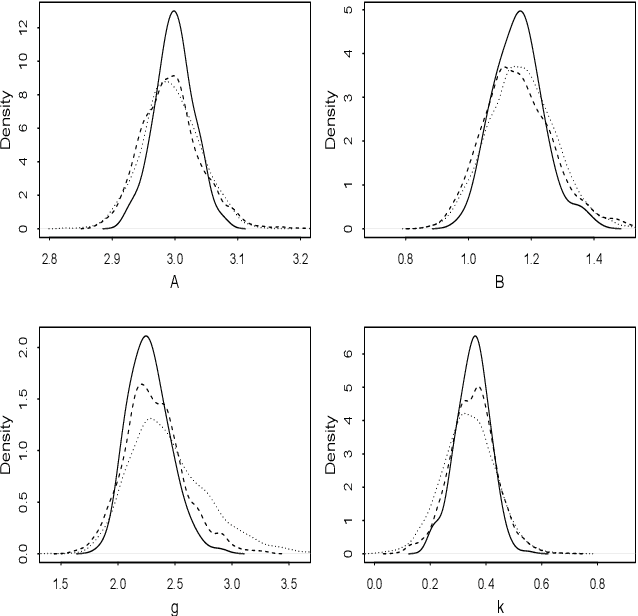
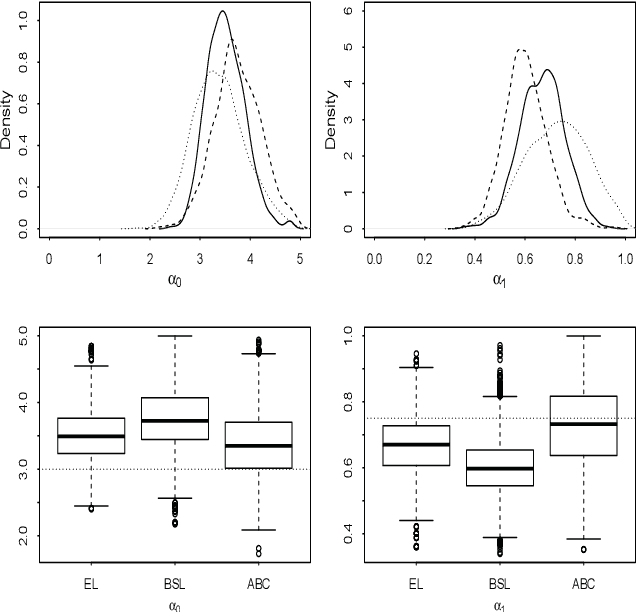
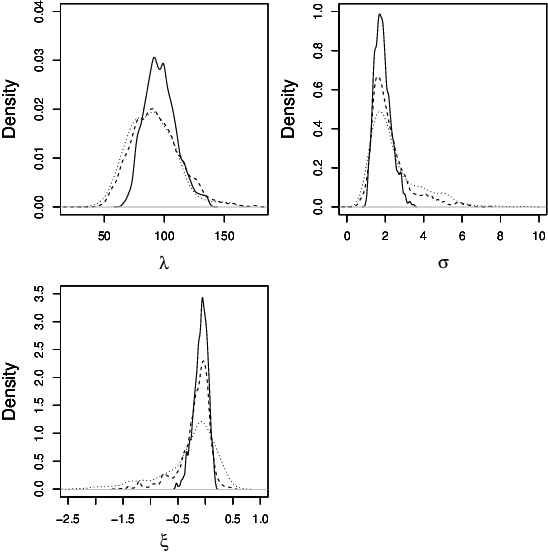
Many scientifically well-motivated statistical models in natural, engineering and environmental sciences are specified through a generative process, but in some cases it may not be possible to write down a likelihood for these models analytically. Approximate Bayesian computation (ABC) methods, which allow Bayesian inference in these situations, are typically computationally intensive. Recently, computationally attractive empirical likelihood based ABC methods have been suggested in the literature. These methods heavily rely on the availability of a set of suitable analytically tractable estimating equations. We propose an easy-to-use empirical likelihood ABC method, where the only inputs required are a choice of summary statistic, it's observed value, and the ability to simulate summary statistics for any parameter value under the model. It is shown that the posterior obtained using the proposed method is consistent, and its performance is explored using various examples.