elhmc: An R Package for Hamiltonian Monte Carlo Sampling in Bayesian Empirical Likelihood

In this article, we describe a {\tt R} package for sampling from an empirical likelihood-based posterior using a Hamiltonian Monte Carlo method. Empirical likelihood-based methodologies have been used in Bayesian modeling of many problems of interest in recent times. This semiparametric procedure can easily combine the flexibility of a non-parametric distribution estimator together with the interpretability of a parametric model. The model is specified by estimating equations-based constraints. Drawing an inference from a Bayesian empirical likelihood (BayesEL) posterior is challenging. The likelihood is computed numerically, so no closed expression of the posterior exists. Moreover, for any sample of finite size, the support of the likelihood is non-convex, which hinders the fast mixing of many Markov Chain Monte Carlo (MCMC) procedures. It has been recently shown that using the properties of the gradient of log empirical likelihood, one can devise an efficient Hamiltonian Monte Carlo (HMC) algorithm to sample from a BayesEL posterior. The package requires the user to specify only the estimating equations, the prior, and their respective gradients. An MCMC sample drawn from the BayesEL posterior of the parameters, with various details required by the user is obtained.

A Two-step Metropolis Hastings Method for Bayesian Empirical Likelihood Computation with Application to Bayesian Model Selection

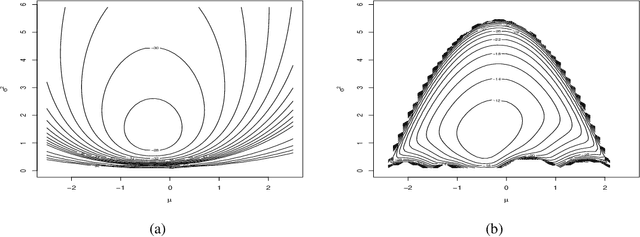
In recent times empirical likelihood has been widely applied under Bayesian framework. Markov chain Monte Carlo (MCMC) methods are frequently employed to sample from the posterior distribution of the parameters of interest. However, complex, especially non-convex nature of the likelihood support erects enormous hindrances in choosing an appropriate MCMC algorithm. Such difficulties have restricted the use of Bayesian empirical likelihood (BayesEL) based methods in many applications. In this article, we propose a two-step Metropolis Hastings algorithm to sample from the BayesEL posteriors. Our proposal is specified hierarchically, where the estimating equations determining the empirical likelihood are used to propose values of a set of parameters depending on the proposed values of the remaining parameters. Furthermore, we discuss Bayesian model selection using empirical likelihood and extend our two-step Metropolis Hastings algorithm to a reversible jump Markov chain Monte Carlo procedure to sample from the resulting posterior. Finally, several applications of our proposed methods are presented.

On a Variational Approximation based Empirical Likelihood ABC Method

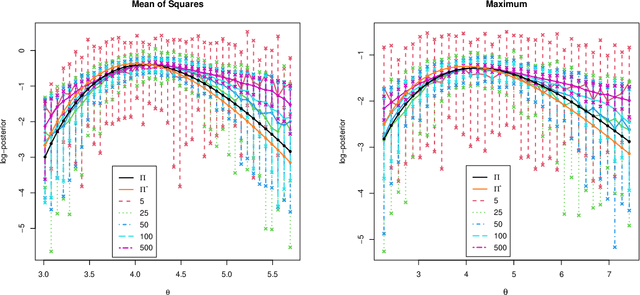
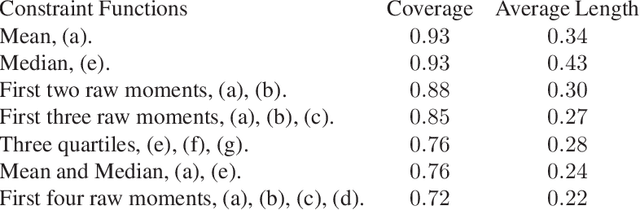
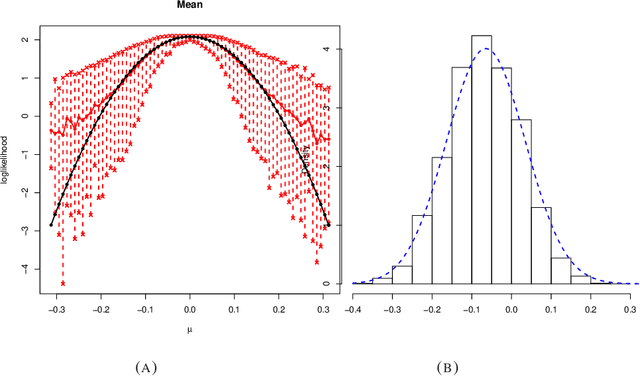
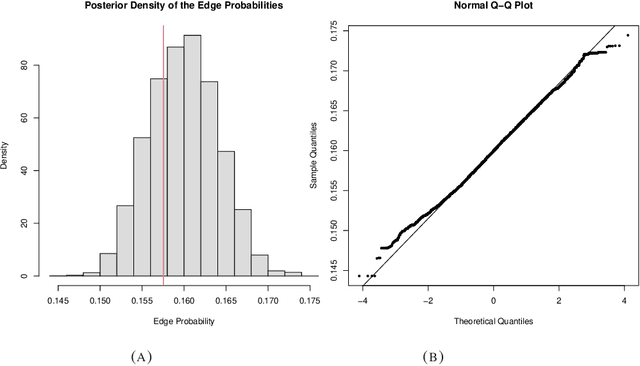
Many scientifically well-motivated statistical models in natural, engineering, and environmental sciences are specified through a generative process. However, in some cases, it may not be possible to write down the likelihood for these models analytically. Approximate Bayesian computation (ABC) methods allow Bayesian inference in such situations. The procedures are nonetheless typically computationally intensive. Recently, computationally attractive empirical likelihood-based ABC methods have been suggested in the literature. All of these methods rely on the availability of several suitable analytically tractable estimating equations, and this is sometimes problematic. We propose an easy-to-use empirical likelihood ABC method in this article. First, by using a variational approximation argument as a motivation, we show that the target log-posterior can be approximated as a sum of an expected joint log-likelihood and the differential entropy of the data generating density. The expected log-likelihood is then estimated by an empirical likelihood where the only inputs required are a choice of summary statistic, it's observed value, and the ability to simulate the chosen summary statistics for any parameter value under the model. The differential entropy is estimated from the simulated summaries using traditional methods. Posterior consistency is established for the method, and we discuss the bounds for the required number of simulated summaries in detail. The performance of the proposed method is explored in various examples.

Empirical Likelihood Under Mis-specification: Degeneracies and Random Critical Points

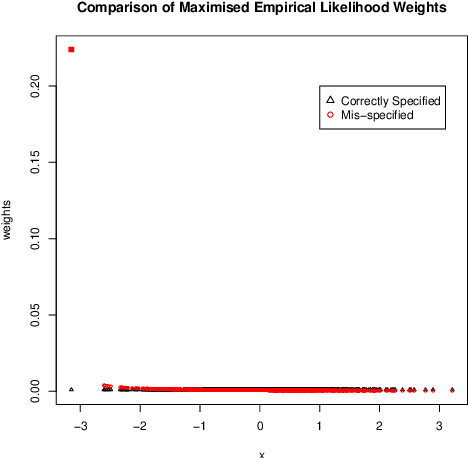
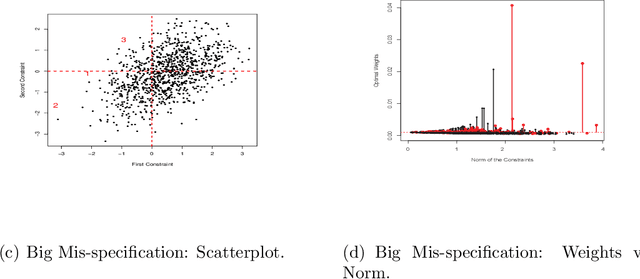
We investigate empirical likelihood obtained from mis-specified (i.e. biased) estimating equations. We establish that the behaviour of the optimal weights under mis-specification differ markedly from their properties under the null, i.e. when the estimating equations are unbiased and correctly specified. This is manifested by certain ``degeneracies'' in the optimal weights which define the likelihood. Such degeneracies in weights are not observed under the null. Furthermore, we establish an anomalous behaviour of the Wilks' statistic, which, unlike under correct specification, does not exhibit a chi-squared limit. In the Bayesian setting, we rigorously establish the posterior consistency of so called BayesEL procedures, where instead of a parametric likelihood, an empirical likelihood is used to define the posterior. In particular, we show that the BayesEL posterior, as a random probability measure, rapidly converges to the delta measure at the true parameter value. A novel feature of our approach is the investigation of critical points of random functions in the context of empirical likelihood. In particular, we obtain the location and the mass of the degenerate optimal weights as the leading and sub-leading terms in a canonical expansion of a particular critical point of a random function that is naturally associated with the model.

An easy-to-use empirical likelihood ABC method

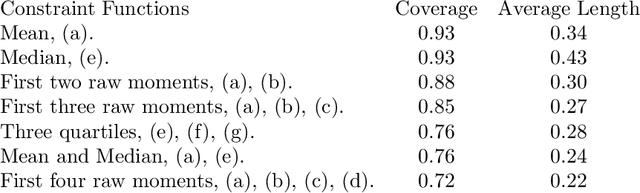
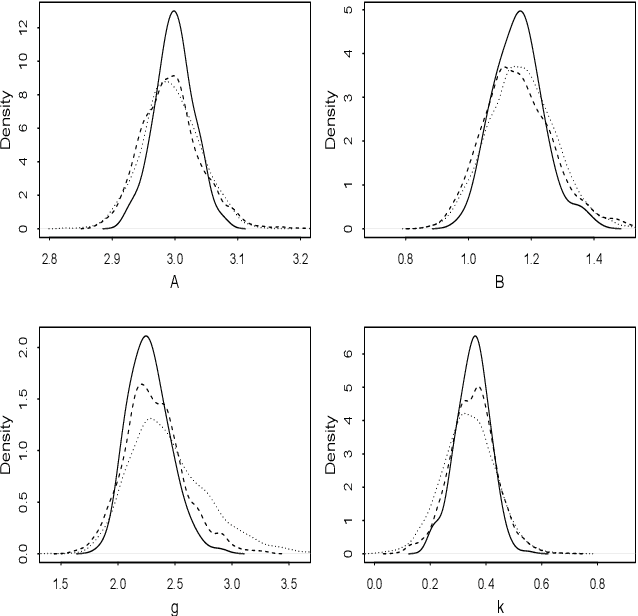
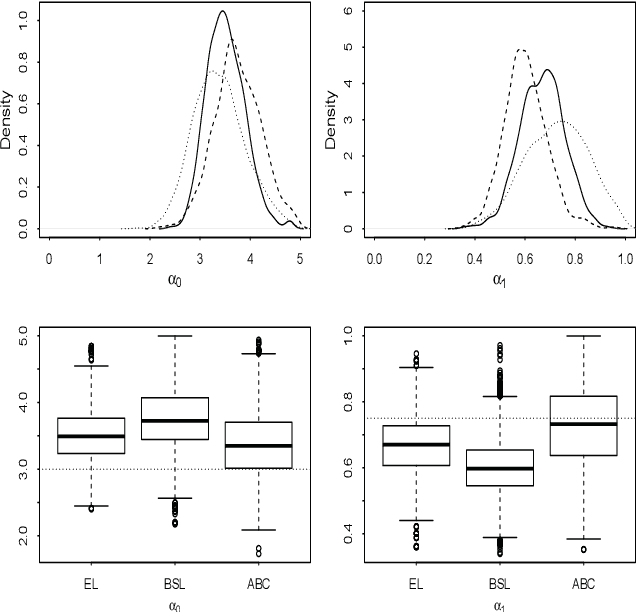
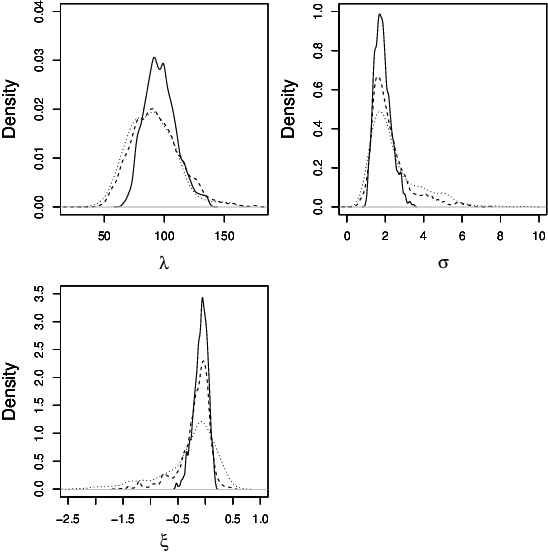
Many scientifically well-motivated statistical models in natural, engineering and environmental sciences are specified through a generative process, but in some cases it may not be possible to write down a likelihood for these models analytically. Approximate Bayesian computation (ABC) methods, which allow Bayesian inference in these situations, are typically computationally intensive. Recently, computationally attractive empirical likelihood based ABC methods have been suggested in the literature. These methods heavily rely on the availability of a set of suitable analytically tractable estimating equations. We propose an easy-to-use empirical likelihood ABC method, where the only inputs required are a choice of summary statistic, it's observed value, and the ability to simulate summary statistics for any parameter value under the model. It is shown that the posterior obtained using the proposed method is consistent, and its performance is explored using various examples.

Qualitative inequalities for squared partial correlations of a Gaussian random vector

We describe various sets of conditional independence relationships, sufficient for qualitatively comparing non-vanishing squared partial correlations of a Gaussian random vector. These sufficient conditions are satisfied by several graphical Markov models. Rules for comparing degree of association among the vertices of such Gaussian graphical models are also developed. We apply these rules to compare conditional dependencies on Gaussian trees. In particular for trees, we show that such dependence can be completely characterized by the length of the paths joining the dependent vertices to each other and to the vertices conditioned on. We also apply our results to postulate rules for model selection for polytree models. Our rules apply to mutual information of Gaussian random vectors as well.