Empirical Likelihood Under Mis-specification: Degeneracies and Random Critical Points

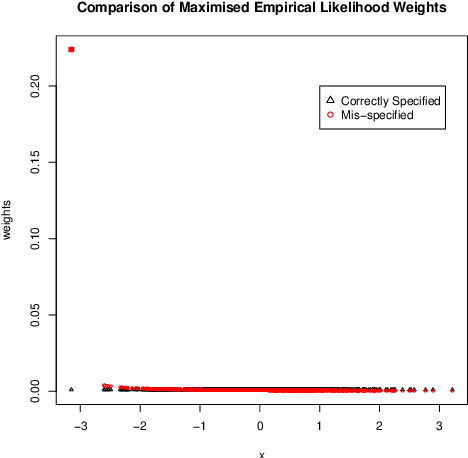
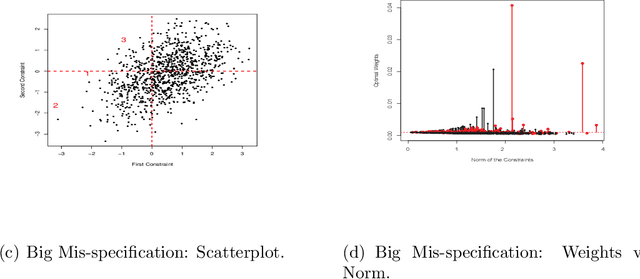
We investigate empirical likelihood obtained from mis-specified (i.e. biased) estimating equations. We establish that the behaviour of the optimal weights under mis-specification differ markedly from their properties under the null, i.e. when the estimating equations are unbiased and correctly specified. This is manifested by certain ``degeneracies'' in the optimal weights which define the likelihood. Such degeneracies in weights are not observed under the null. Furthermore, we establish an anomalous behaviour of the Wilks' statistic, which, unlike under correct specification, does not exhibit a chi-squared limit. In the Bayesian setting, we rigorously establish the posterior consistency of so called BayesEL procedures, where instead of a parametric likelihood, an empirical likelihood is used to define the posterior. In particular, we show that the BayesEL posterior, as a random probability measure, rapidly converges to the delta measure at the true parameter value. A novel feature of our approach is the investigation of critical points of random functions in the context of empirical likelihood. In particular, we obtain the location and the mass of the degenerate optimal weights as the leading and sub-leading terms in a canonical expansion of a particular critical point of a random function that is naturally associated with the model.