PGAD: Prototype-Guided Adaptive Distillation for Multi-Modal Learning in AD Diagnosis

Missing modalities pose a major issue in Alzheimer's Disease (AD) diagnosis, as many subjects lack full imaging data due to cost and clinical constraints. While multi-modal learning leverages complementary information, most existing methods train only on complete data, ignoring the large proportion of incomplete samples in real-world datasets like ADNI. This reduces the effective training set and limits the full use of valuable medical data. While some methods incorporate incomplete samples, they fail to effectively address inter-modal feature alignment and knowledge transfer challenges under high missing rates. To address this, we propose a Prototype-Guided Adaptive Distillation (PGAD) framework that directly incorporates incomplete multi-modal data into training. PGAD enhances missing modality representations through prototype matching and balances learning with a dynamic sampling strategy. We validate PGAD on the ADNI dataset with varying missing rates (20%, 50%, and 70%) and demonstrate that it significantly outperforms state-of-the-art approaches. Ablation studies confirm the effectiveness of prototype matching and adaptive sampling, highlighting the potential of our framework for robust and scalable AD diagnosis in real-world clinical settings.

A Two-step Metropolis Hastings Method for Bayesian Empirical Likelihood Computation with Application to Bayesian Model Selection

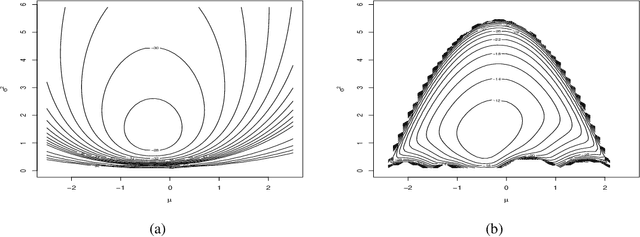
In recent times empirical likelihood has been widely applied under Bayesian framework. Markov chain Monte Carlo (MCMC) methods are frequently employed to sample from the posterior distribution of the parameters of interest. However, complex, especially non-convex nature of the likelihood support erects enormous hindrances in choosing an appropriate MCMC algorithm. Such difficulties have restricted the use of Bayesian empirical likelihood (BayesEL) based methods in many applications. In this article, we propose a two-step Metropolis Hastings algorithm to sample from the BayesEL posteriors. Our proposal is specified hierarchically, where the estimating equations determining the empirical likelihood are used to propose values of a set of parameters depending on the proposed values of the remaining parameters. Furthermore, we discuss Bayesian model selection using empirical likelihood and extend our two-step Metropolis Hastings algorithm to a reversible jump Markov chain Monte Carlo procedure to sample from the resulting posterior. Finally, several applications of our proposed methods are presented.