David T. Frazier
Predictively Oriented Posteriors
Oct 02, 2025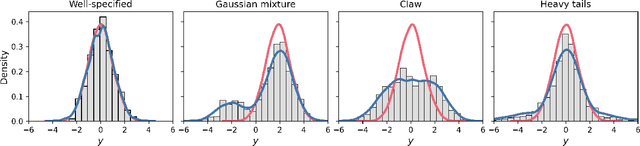
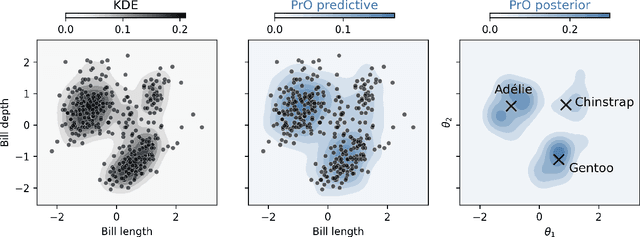
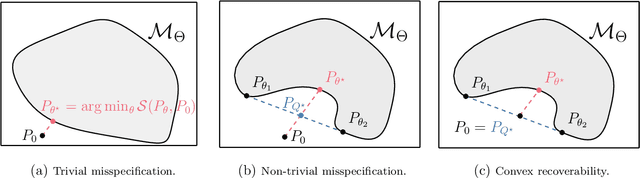
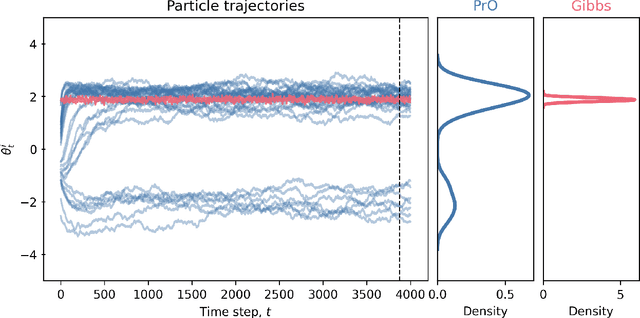
Abstract:We advocate for a new statistical principle that combines the most desirable aspects of both parameter inference and density estimation. This leads us to the predictively oriented (PrO) posterior, which expresses uncertainty as a consequence of predictive ability. Doing so leads to inferences which predictively dominate both classical and generalised Bayes posterior predictive distributions: up to logarithmic factors, PrO posteriors converge to the predictively optimal model average at rate $n^{-1/2}$. Whereas classical and generalised Bayes posteriors only achieve this rate if the model can recover the data-generating process, PrO posteriors adapt to the level of model misspecification. This means that they concentrate around the true model at rate $n^{1/2}$ in the same way as Bayes and Gibbs posteriors if the model can recover the data-generating distribution, but do \textit{not} concentrate in the presence of non-trivial forms of model misspecification. Instead, they stabilise towards a predictively optimal posterior whose degree of irreducible uncertainty admits an interpretation as the degree of model misspecification -- a sharp contrast to how Bayesian uncertainty and its existing extensions behave. Lastly, we show that PrO posteriors can be sampled from by evolving particles based on mean field Langevin dynamics, and verify the practical significance of our theoretical developments on a number of numerical examples.
Simulation-based Bayesian inference under model misspecification
Mar 16, 2025Abstract:Simulation-based Bayesian inference (SBI) methods are widely used for parameter estimation in complex models where evaluating the likelihood is challenging but generating simulations is relatively straightforward. However, these methods commonly assume that the simulation model accurately reflects the true data-generating process, an assumption that is frequently violated in realistic scenarios. In this paper, we focus on the challenges faced by SBI methods under model misspecification. We consolidate recent research aimed at mitigating the effects of misspecification, highlighting three key strategies: i) robust summary statistics, ii) generalised Bayesian inference, and iii) error modelling and adjustment parameters. To illustrate both the vulnerabilities of popular SBI methods and the effectiveness of misspecification-robust alternatives, we present empirical results on an illustrative example.
The Statistical Accuracy of Neural Posterior and Likelihood Estimation
Nov 18, 2024



Abstract:Neural posterior estimation (NPE) and neural likelihood estimation (NLE) are machine learning approaches that provide accurate posterior, and likelihood, approximations in complex modeling scenarios, and in situations where conducting amortized inference is a necessity. While such methods have shown significant promise across a range of diverse scientific applications, the statistical accuracy of these methods is so far unexplored. In this manuscript, we give, for the first time, an in-depth exploration on the statistical behavior of NPE and NLE. We prove that these methods have similar theoretical guarantees to common statistical methods like approximate Bayesian computation (ABC) and Bayesian synthetic likelihood (BSL). While NPE and NLE methods are just as accurate as ABC and BSL, we prove that this accuracy can often be achieved at a vastly reduced computational cost, and will therefore deliver more attractive approximations than ABC and BSL in certain problems. We verify our results theoretically and in several examples from the literature.
Misspecification-robust Sequential Neural Likelihood
Jan 31, 2023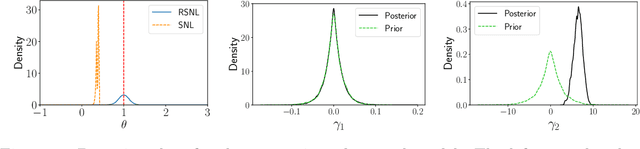
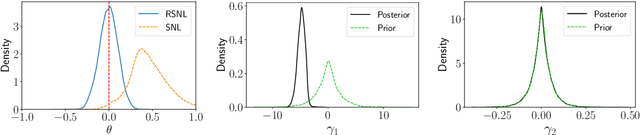
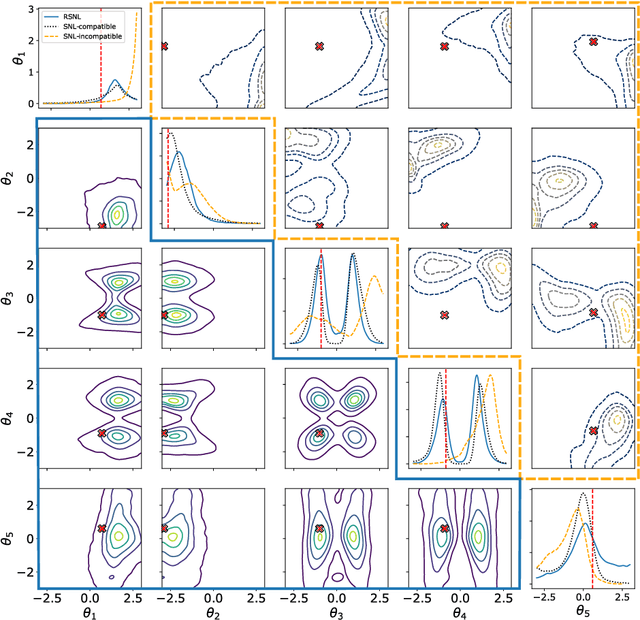
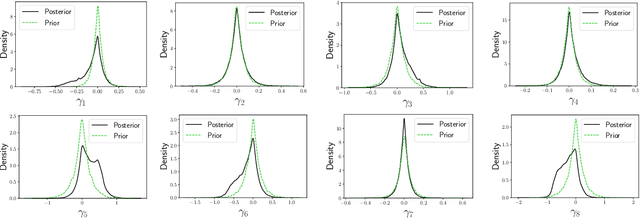
Abstract:Simulation-based inference (SBI) techniques are now an essential tool for the parameter estimation of mechanistic and simulatable models with intractable likelihoods. Statistical approaches to SBI such as approximate Bayesian computation and Bayesian synthetic likelihood have been well studied in the well specified and misspecified settings. However, most implementations are inefficient in that many model simulations are wasted. Neural approaches such as sequential neural likelihood (SNL) have been developed that exploit all model simulations to build a surrogate of the likelihood function. However, SNL approaches have been shown to perform poorly under model misspecification. In this paper, we develop a new method for SNL that is robust to model misspecification and can identify areas where the model is deficient. We demonstrate the usefulness of the new approach on several illustrative examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge