T. Rodrigues
University of Brasília
Positional Encoder Graph Quantile Neural Networks for Geographic Data
Sep 27, 2024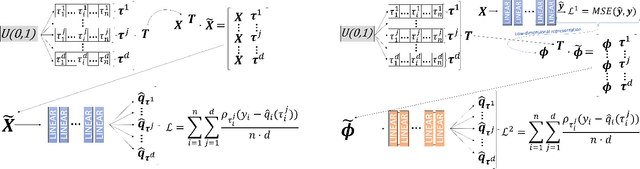
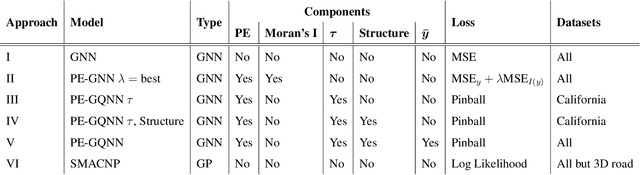
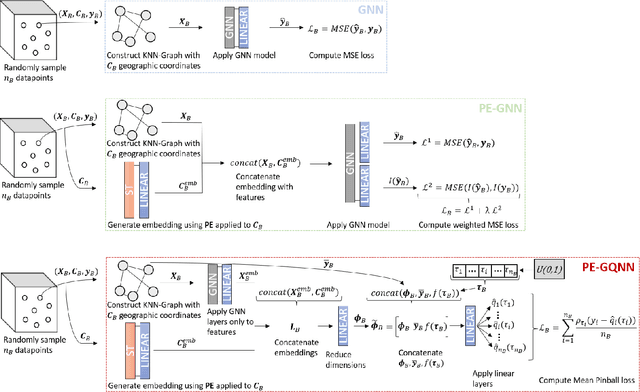
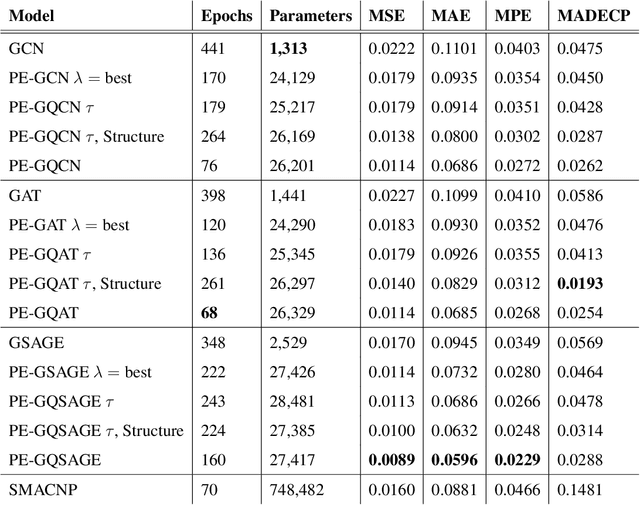
Abstract:Positional Encoder Graph Neural Networks (PE-GNNs) are a leading approach for modeling continuous spatial data. However, they often fail to produce calibrated predictive distributions, limiting their effectiveness for uncertainty quantification. We introduce the Positional Encoder Graph Quantile Neural Network (PE-GQNN), a novel method that integrates PE-GNNs, Quantile Neural Networks, and recalibration techniques in a fully nonparametric framework, requiring minimal assumptions about the predictive distributions. We propose a new network architecture that, when combined with a quantile-based loss function, yields accurate and reliable probabilistic models without increasing computational complexity. Our approach provides a flexible, robust framework for conditional density estimation, applicable beyond spatial data contexts. We further introduce a structured method for incorporating a KNN predictor into the model while avoiding data leakage through the GNN layer operation. Experiments on benchmark datasets demonstrate that PE-GQNN significantly outperforms existing state-of-the-art methods in both predictive accuracy and uncertainty quantification.
Model-Free Local Recalibration of Neural Networks
Mar 09, 2024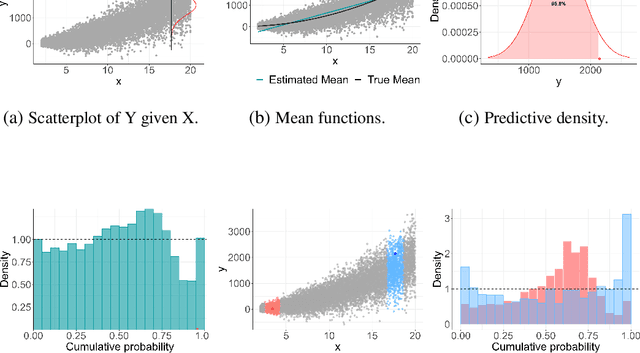


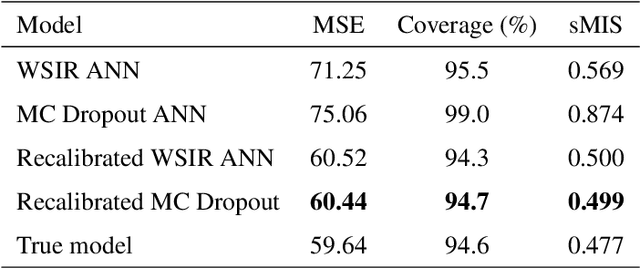
Abstract:Artificial neural networks (ANNs) are highly flexible predictive models. However, reliably quantifying uncertainty for their predictions is a continuing challenge. There has been much recent work on "recalibration" of predictive distributions for ANNs, so that forecast probabilities for events of interest are consistent with certain frequency evaluations of them. Uncalibrated probabilistic forecasts are of limited use for many important decision-making tasks. To address this issue, we propose a localized recalibration of ANN predictive distributions using the dimension-reduced representation of the input provided by the ANN hidden layers. Our novel method draws inspiration from recalibration techniques used in the literature on approximate Bayesian computation and likelihood-free inference methods. Most existing calibration methods for ANNs can be thought of as calibrating either on the input layer, which is difficult when the input is high-dimensional, or the output layer, which may not be sufficiently flexible. Through a simulation study, we demonstrate that our method has good performance compared to alternative approaches, and explore the benefits that can be achieved by localizing the calibration based on different layers of the network. Finally, we apply our proposed method to a diamond price prediction problem, demonstrating the potential of our approach to improve prediction and uncertainty quantification in real-world applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge