Model-Free Local Recalibration of Neural Networks

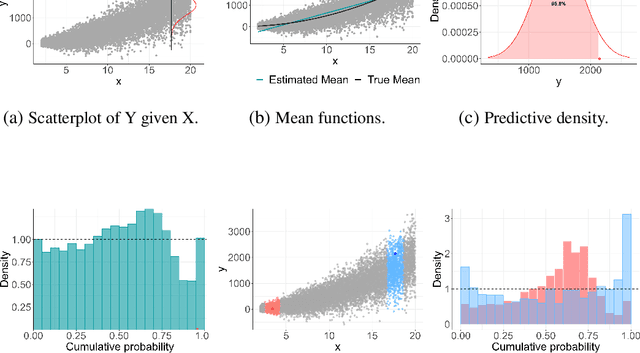
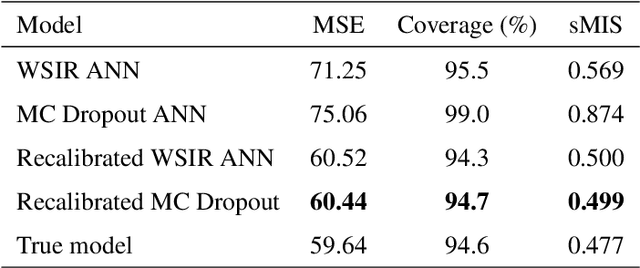
Artificial neural networks (ANNs) are highly flexible predictive models. However, reliably quantifying uncertainty for their predictions is a continuing challenge. There has been much recent work on "recalibration" of predictive distributions for ANNs, so that forecast probabilities for events of interest are consistent with certain frequency evaluations of them. Uncalibrated probabilistic forecasts are of limited use for many important decision-making tasks. To address this issue, we propose a localized recalibration of ANN predictive distributions using the dimension-reduced representation of the input provided by the ANN hidden layers. Our novel method draws inspiration from recalibration techniques used in the literature on approximate Bayesian computation and likelihood-free inference methods. Most existing calibration methods for ANNs can be thought of as calibrating either on the input layer, which is difficult when the input is high-dimensional, or the output layer, which may not be sufficiently flexible. Through a simulation study, we demonstrate that our method has good performance compared to alternative approaches, and explore the benefits that can be achieved by localizing the calibration based on different layers of the network. Finally, we apply our proposed method to a diamond price prediction problem, demonstrating the potential of our approach to improve prediction and uncertainty quantification in real-world applications.

Likelihood-free approximate Gibbs sampling

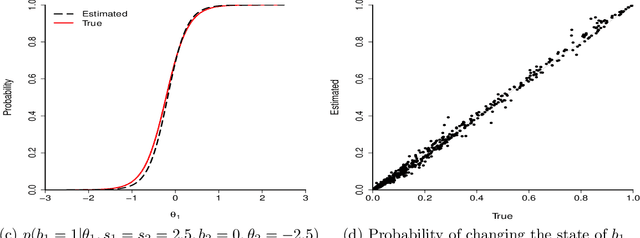
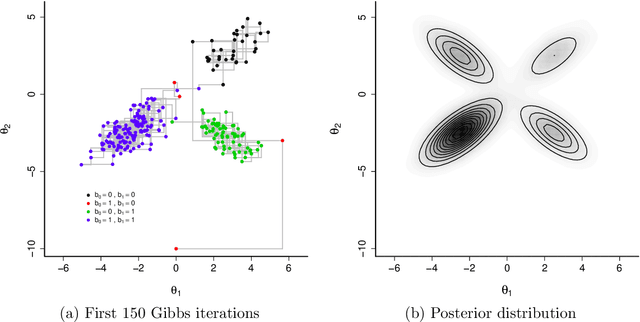
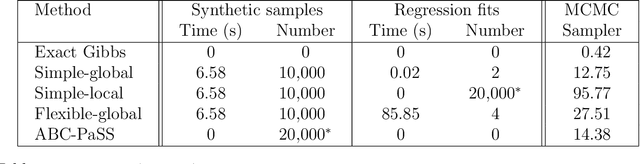
Likelihood-free methods such as approximate Bayesian computation (ABC) have extended the reach of statistical inference to problems with computationally intractable likelihoods. Such approaches perform well for small-to-moderate dimensional problems, but suffer a curse of dimensionality in the number of model parameters. We introduce a likelihood-free approximate Gibbs sampler that naturally circumvents the dimensionality issue by focusing on lower-dimensional conditional distributions. These distributions are estimated by flexible regression models either before the sampler is run, or adaptively during sampler implementation. As a result, and in comparison to Metropolis-Hastings based approaches, we are able to fit substantially more challenging statistical models than would otherwise be possible. We demonstrate the sampler's performance via two simulated examples, and a real analysis of Airbnb rental prices using a intractable high-dimensional multivariate non-linear state space model containing 13,140 parameters, which presents a real challenge to standard ABC techniques.

High-dimensional ABC

This Chapter, "High-dimensional ABC", is to appear in the forthcoming Handbook of Approximate Bayesian Computation (2018). It details the main ideas and concepts behind extending ABC methods to higher dimensions, with supporting examples and illustrations.

Overview of Approximate Bayesian Computation

This Chapter, "Overview of Approximate Bayesian Computation", is to appear as the first chapter in the forthcoming Handbook of Approximate Bayesian Computation (2018). It details the main ideas and concepts behind ABC methods with many examples and illustrations.

ABC Samplers

This Chapter, "ABC Samplers", is to appear in the forthcoming Handbook of Approximate Bayesian Computation (2018). It details the main ideas and algorithms used to sample from the ABC approximation to the posterior distribution, including methods based on rejection/importance sampling, MCMC and sequential Monte Carlo.