Likelihood-free approximate Gibbs sampling
Paper and Code
Jun 11, 2019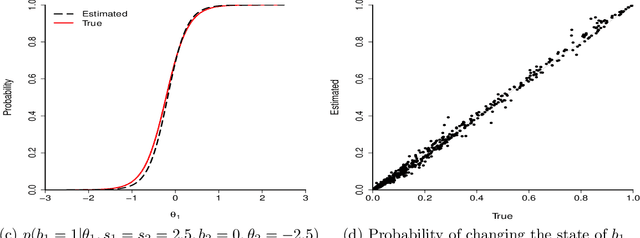

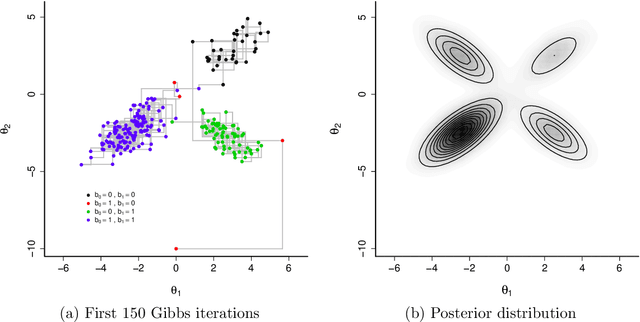
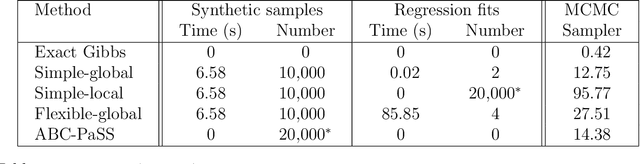
Likelihood-free methods such as approximate Bayesian computation (ABC) have extended the reach of statistical inference to problems with computationally intractable likelihoods. Such approaches perform well for small-to-moderate dimensional problems, but suffer a curse of dimensionality in the number of model parameters. We introduce a likelihood-free approximate Gibbs sampler that naturally circumvents the dimensionality issue by focusing on lower-dimensional conditional distributions. These distributions are estimated by flexible regression models either before the sampler is run, or adaptively during sampler implementation. As a result, and in comparison to Metropolis-Hastings based approaches, we are able to fit substantially more challenging statistical models than would otherwise be possible. We demonstrate the sampler's performance via two simulated examples, and a real analysis of Airbnb rental prices using a intractable high-dimensional multivariate non-linear state space model containing 13,140 parameters, which presents a real challenge to standard ABC techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge