A Unified Framework for Variable Selection in Model-Based Clustering with Missing Not at Random

Model-based clustering integrated with variable selection is a powerful tool for uncovering latent structures within complex data. However, its effectiveness is often hindered by challenges such as identifying relevant variables that define heterogeneous subgroups and handling data that are missing not at random, a prevalent issue in fields like transcriptomics. While several notable methods have been proposed to address these problems, they typically tackle each issue in isolation, thereby limiting their flexibility and adaptability. This paper introduces a unified framework designed to address these challenges simultaneously. Our approach incorporates a data-driven penalty matrix into penalized clustering to enable more flexible variable selection, along with a mechanism that explicitly models the relationship between missingness and latent class membership. We demonstrate that, under certain regularity conditions, the proposed framework achieves both asymptotic consistency and selection consistency, even in the presence of missing data. This unified strategy significantly enhances the capability and efficiency of model-based clustering, advancing methodologies for identifying informative variables that define homogeneous subgroups in the presence of complex missing data patterns. The performance of the framework, including its computational efficiency, is evaluated through simulations and demonstrated using both synthetic and real-world transcriptomic datasets.

Model Selection for Gaussian-gated Gaussian Mixture of Experts Using Dendrograms of Mixing Measures

Mixture of Experts (MoE) models constitute a widely utilized class of ensemble learning approaches in statistics and machine learning, known for their flexibility and computational efficiency. They have become integral components in numerous state-of-the-art deep neural network architectures, particularly for analyzing heterogeneous data across diverse domains. Despite their practical success, the theoretical understanding of model selection, especially concerning the optimal number of mixture components or experts, remains limited and poses significant challenges. These challenges primarily stem from the inclusion of covariates in both the Gaussian gating functions and expert networks, which introduces intrinsic interactions governed by partial differential equations with respect to their parameters. In this paper, we revisit the concept of dendrograms of mixing measures and introduce a novel extension to Gaussian-gated Gaussian MoE models that enables consistent estimation of the true number of mixture components and achieves the pointwise optimal convergence rate for parameter estimation in overfitted scenarios. Notably, this approach circumvents the need to train and compare a range of models with varying numbers of components, thereby alleviating the computational burden, particularly in high-dimensional or deep neural network settings. Experimental results on synthetic data demonstrate the effectiveness of the proposed method in accurately recovering the number of experts. It outperforms common criteria such as the Akaike information criterion, the Bayesian information criterion, and the integrated completed likelihood, while achieving optimal convergence rates for parameter estimation and accurately approximating the regression function.

LoGra-Med: Long Context Multi-Graph Alignment for Medical Vision-Language Model

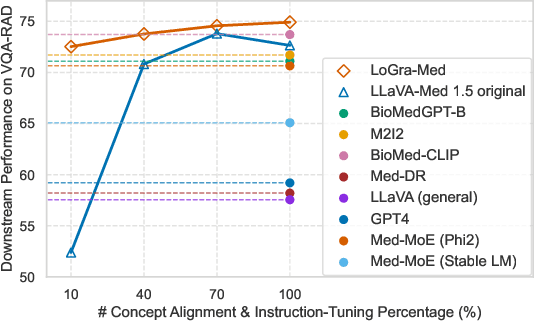
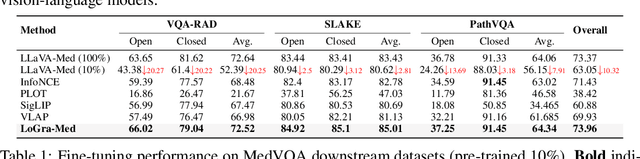
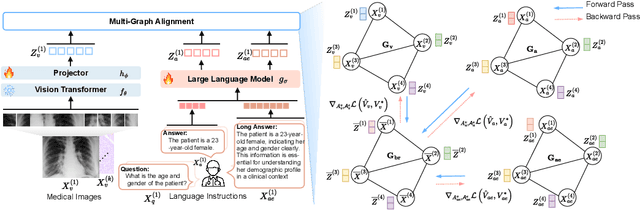
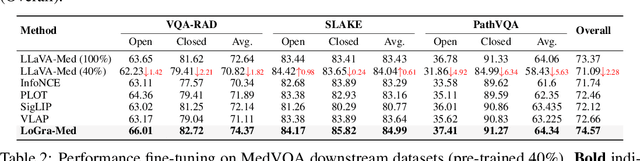
State-of-the-art medical multi-modal large language models (med-MLLM), like LLaVA-Med or BioMedGPT, leverage instruction-following data in pre-training. However, those models primarily focus on scaling the model size and data volume to boost performance while mainly relying on the autoregressive learning objectives. Surprisingly, we reveal that such learning schemes might result in a weak alignment between vision and language modalities, making these models highly reliant on extensive pre-training datasets - a significant challenge in medical domains due to the expensive and time-consuming nature of curating high-quality instruction-following instances. We address this with LoGra-Med, a new multi-graph alignment algorithm that enforces triplet correlations across image modalities, conversation-based descriptions, and extended captions. This helps the model capture contextual meaning, handle linguistic variability, and build cross-modal associations between visuals and text. To scale our approach, we designed an efficient end-to-end learning scheme using black-box gradient estimation, enabling faster LLaMa 7B training. Our results show LoGra-Med matches LLAVA-Med performance on 600K image-text pairs for Medical VQA and significantly outperforms it when trained on 10% of the data. For example, on VQA-RAD, we exceed LLAVA-Med by 20.13% and nearly match the 100% pre-training score (72.52% vs. 72.64%). We also surpass SOTA methods like BiomedGPT on visual chatbots and RadFM on zero-shot image classification with VQA, highlighting the effectiveness of multi-graph alignment.

Risk Bounds for Mixture Density Estimation on Compact Domains via the $h$-Lifted Kullback--Leibler Divergence

We consider the problem of estimating probability density functions based on sample data, using a finite mixture of densities from some component class. To this end, we introduce the $h$-lifted Kullback--Leibler (KL) divergence as a generalization of the standard KL divergence and a criterion for conducting risk minimization. Under a compact support assumption, we prove an $\mc{O}(1/{\sqrt{n}})$ bound on the expected estimation error when using the $h$-lifted KL divergence, which extends the results of Rakhlin et al. (2005, ESAIM: Probability and Statistics, Vol. 9) and Li and Barron (1999, Advances in Neural Information ProcessingSystems, Vol. 12) to permit the risk bounding of density functions that are not strictly positive. We develop a procedure for the computation of the corresponding maximum $h$-lifted likelihood estimators ($h$-MLLEs) using the Majorization-Maximization framework and provide experimental results in support of our theoretical bounds.

CompeteSMoE -- Effective Training of Sparse Mixture of Experts via Competition

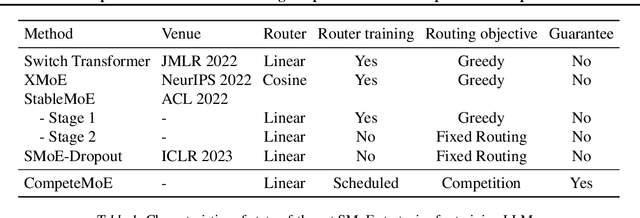
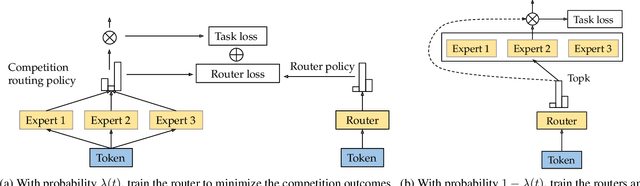
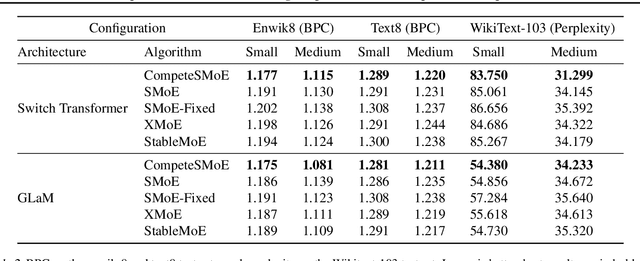
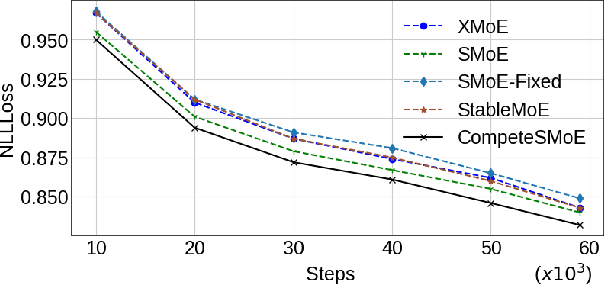
Sparse mixture of experts (SMoE) offers an appealing solution to scale up the model complexity beyond the mean of increasing the network's depth or width. However, effective training of SMoE has proven to be challenging due to the representation collapse issue, which causes parameter redundancy and limited representation potentials. In this work, we propose a competition mechanism to address this fundamental challenge of representation collapse. By routing inputs only to experts with the highest neural response, we show that, under mild assumptions, competition enjoys the same convergence rate as the optimal estimator. We further propose CompeteSMoE, an effective and efficient algorithm to train large language models by deploying a simple router that predicts the competition outcomes. Consequently, CompeteSMoE enjoys strong performance gains from the competition routing policy while having low computation overheads. Our extensive empirical evaluations on two transformer architectures and a wide range of tasks demonstrate the efficacy, robustness, and scalability of CompeteSMoE compared to state-of-the-art SMoE strategies.

Structure-Aware E(3)-Invariant Molecular Conformer Aggregation Networks

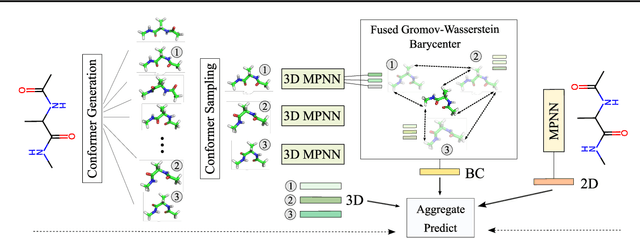
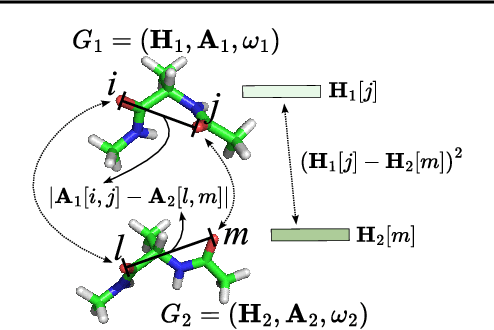
A molecule's 2D representation consists of its atoms, their attributes, and the molecule's covalent bonds. A 3D (geometric) representation of a molecule is called a conformer and consists of its atom types and Cartesian coordinates. Every conformer has a potential energy, and the lower this energy, the more likely it occurs in nature. Most existing machine learning methods for molecular property prediction consider either 2D molecular graphs or 3D conformer structure representations in isolation. Inspired by recent work on using ensembles of conformers in conjunction with 2D graph representations, we propose E(3)-invariant molecular conformer aggregation networks. The method integrates a molecule's 2D representation with that of multiple of its conformers. Contrary to prior work, we propose a novel 2D--3D aggregation mechanism based on a differentiable solver for the \emph{Fused Gromov-Wasserstein Barycenter} problem and the use of an efficient online conformer generation method based on distance geometry. We show that the proposed aggregation mechanism is E(3) invariant and provides an efficient GPU implementation. Moreover, we demonstrate that the aggregation mechanism helps to outperform state-of-the-art property prediction methods on established datasets significantly.

HyperRouter: Towards Efficient Training and Inference of Sparse Mixture of Experts

By routing input tokens to only a few split experts, Sparse Mixture-of-Experts has enabled efficient training of large language models. Recent findings suggest that fixing the routers can achieve competitive performance by alleviating the collapsing problem, where all experts eventually learn similar representations. However, this strategy has two key limitations: (i) the policy derived from random routers might be sub-optimal, and (ii) it requires extensive resources during training and evaluation, leading to limited efficiency gains. This work introduces \HyperRout, which dynamically generates the router's parameters through a fixed hypernetwork and trainable embeddings to achieve a balance between training the routers and freezing them to learn an improved routing policy. Extensive experiments across a wide range of tasks demonstrate the superior performance and efficiency gains of \HyperRouter compared to existing routing methods. Our implementation is publicly available at {\url{{https://github.com/giangdip2410/HyperRouter}}}.

A General Theory for Softmax Gating Multinomial Logistic Mixture of Experts

Mixture-of-experts (MoE) model incorporates the power of multiple submodels via gating functions to achieve greater performance in numerous regression and classification applications. From a theoretical perspective, while there have been previous attempts to comprehend the behavior of that model under the regression settings through the convergence analysis of maximum likelihood estimation in the Gaussian MoE model, such analysis under the setting of a classification problem has remained missing in the literature. We close this gap by establishing the convergence rates of density estimation and parameter estimation in the softmax gating multinomial logistic MoE model. Notably, when part of the expert parameters vanish, these rates are shown to be slower than polynomial rates owing to an inherent interaction between the softmax gating and expert functions via partial differential equations. To address this issue, we propose using a novel class of modified softmax gating functions which transform the input value before delivering them to the gating functions. As a result, the previous interaction disappears and the parameter estimation rates are significantly improved.

Towards Convergence Rates for Parameter Estimation in Gaussian-gated Mixture of Experts

Originally introduced as a neural network for ensemble learning, mixture of experts (MoE) has recently become a fundamental building block of highly successful modern deep neural networks for heterogeneous data analysis in several applications, including those in machine learning, statistics, bioinformatics, economics, and medicine. Despite its popularity in practice, a satisfactory level of understanding of the convergence behavior of Gaussian-gated MoE parameter estimation is far from complete. The underlying reason for this challenge is the inclusion of covariates in the Gaussian gating and expert networks, which leads to their intrinsically complex interactions via partial differential equations with respect to their parameters. We address these issues by designing novel Voronoi loss functions to accurately capture heterogeneity in the maximum likelihood estimator (MLE) for resolving parameter estimation in these models. Our results reveal distinct behaviors of the MLE under two settings: the first setting is when all the location parameters in the Gaussian gating are non-zeros while the second setting is when there exists at least one zero-valued location parameter. Notably, these behaviors can be characterized by the solvability of two different systems of polynomial equations. Finally, we conduct a simulation study to verify our theoretical results.

Demystifying Softmax Gating in Gaussian Mixture of Experts

Understanding parameter estimation of softmax gating Gaussian mixture of experts has remained a long-standing open problem in the literature. It is mainly due to three fundamental theoretical challenges associated with the softmax gating: (i) the identifiability only up to the translation of the parameters; (ii) the intrinsic interaction via partial differential equation between the softmax gating and the expert functions in Gaussian distribution; (iii) the complex dependence between the numerator and denominator of the conditional density of softmax gating Gaussian mixture of experts. We resolve these challenges by proposing novel Vononoi loss functions among parameters and establishing the convergence rates of the maximum likelihood estimator (MLE) for solving parameter estimation in these models. When the number of experts is unknown and over-specified, our findings show a connection between the rate of MLE and a solvability problem of a system of polynomial equations.