On Minimax Estimation of Parameters in Softmax-Contaminated Mixture of Experts

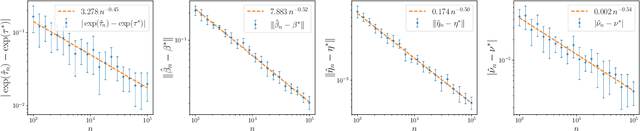
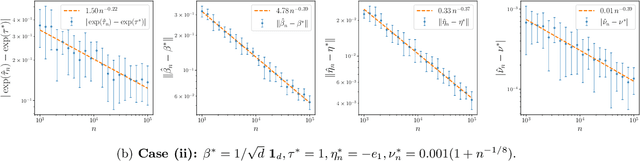
The softmax-contaminated mixture of experts (MoE) model is deployed when a large-scale pre-trained model, which plays the role of a fixed expert, is fine-tuned for learning downstream tasks by including a new contamination part, or prompt, functioning as a new, trainable expert. Despite its popularity and relevance, the theoretical properties of the softmax-contaminated MoE have remained unexplored in the literature. In the paper, we study the convergence rates of the maximum likelihood estimator of gating and prompt parameters in order to gain insights into the statistical properties and potential challenges of fine-tuning with a new prompt. We find that the estimability of these parameters is compromised when the prompt acquires overlapping knowledge with the pre-trained model, in the sense that we make precise by formulating a novel analytic notion of distinguishability. Under distinguishability of the pre-trained and prompt models, we derive minimax optimal estimation rates for all the gating and prompt parameters. By contrast, when the distinguishability condition is violated, these estimation rates become significantly slower due to their dependence on the prompt convergence rate to the pre-trained model. Finally, we empirically corroborate our theoretical findings through several numerical experiments.

Understanding Expert Structures on Minimax Parameter Estimation in Contaminated Mixture of Experts

We conduct the convergence analysis of parameter estimation in the contaminated mixture of experts. This model is motivated from the prompt learning problem where ones utilize prompts, which can be formulated as experts, to fine-tune a large-scaled pre-trained model for learning downstream tasks. There are two fundamental challenges emerging from the analysis: (i) the proportion in the mixture of the pre-trained model and the prompt may converge to zero where the prompt vanishes during the training; (ii) the algebraic interaction among parameters of the pre-trained model and the prompt can occur via some partial differential equation and decelerate the prompt learning. In response, we introduce a distinguishability condition to control the previous parameter interaction. Additionally, we also consider various types of expert structures to understand their effects on the parameter estimation. In each scenario, we provide comprehensive convergence rates of parameter estimation along with the corresponding minimax lower bounds.

Quadratic Gating Functions in Mixture of Experts: A Statistical Insight

Mixture of Experts (MoE) models are highly effective in scaling model capacity while preserving computational efficiency, with the gating network, or router, playing a central role by directing inputs to the appropriate experts. In this paper, we establish a novel connection between MoE frameworks and attention mechanisms, demonstrating how quadratic gating can serve as a more expressive and efficient alternative. Motivated by this insight, we explore the implementation of quadratic gating within MoE models, identifying a connection between the self-attention mechanism and the quadratic gating. We conduct a comprehensive theoretical analysis of the quadratic softmax gating MoE framework, showing improved sample efficiency in expert and parameter estimation. Our analysis provides key insights into optimal designs for quadratic gating and expert functions, further elucidating the principles behind widely used attention mechanisms. Through extensive evaluations, we demonstrate that the quadratic gating MoE outperforms the traditional linear gating MoE. Moreover, our theoretical insights have guided the development of a novel attention mechanism, which we validated through extensive experiments. The results demonstrate its favorable performance over conventional models across various tasks.

Statistical Advantages of Perturbing Cosine Router in Sparse Mixture of Experts

The cosine router in sparse Mixture of Experts (MoE) has recently emerged as an attractive alternative to the conventional linear router. Indeed, the cosine router demonstrates favorable performance in image and language tasks and exhibits better ability to mitigate the representation collapse issue, which often leads to parameter redundancy and limited representation potentials. Despite its empirical success, a comprehensive analysis of the cosine router in sparse MoE has been lacking. Considering the least square estimation of the cosine routing sparse MoE, we demonstrate that due to the intrinsic interaction of the model parameters in the cosine router via some partial differential equations, regardless of the structures of the experts, the estimation rates of experts and model parameters can be as slow as $\mathcal{O}(1/\log^{\tau}(n))$ where $\tau > 0$ is some constant and $n$ is the sample size. Surprisingly, these pessimistic non-polynomial convergence rates can be circumvented by the widely used technique in practice to stabilize the cosine router -- simply adding noises to the $\mathbb{L}_{2}$ norms in the cosine router, which we refer to as \textit{perturbed cosine router}. Under the strongly identifiable settings of the expert functions, we prove that the estimation rates for both the experts and model parameters under the perturbed cosine routing sparse MoE are significantly improved to polynomial rates. Finally, we conduct extensive simulation studies in both synthetic and real data settings to empirically validate our theoretical results.

Is Temperature Sample Efficient for Softmax Gaussian Mixture of Experts?

Dense-to-sparse gating mixture of experts (MoE) has recently become an effective alternative to a well-known sparse MoE. Rather than fixing the number of activated experts as in the latter model, which could limit the investigation of potential experts, the former model utilizes the temperature to control the softmax weight distribution and the sparsity of the MoE during training in order to stabilize the expert specialization. Nevertheless, while there are previous attempts to theoretically comprehend the sparse MoE, a comprehensive analysis of the dense-to-sparse gating MoE has remained elusive. Therefore, we aim to explore the impacts of the dense-to-sparse gate on the maximum likelihood estimation under the Gaussian MoE in this paper. We demonstrate that due to interactions between the temperature and other model parameters via some partial differential equations, the convergence rates of parameter estimations are slower than any polynomial rates, and could be as slow as $\mathcal{O}(1/\log(n))$, where $n$ denotes the sample size. To address this issue, we propose using a novel activation dense-to-sparse gate, which routes the output of a linear layer to an activation function before delivering them to the softmax function. By imposing linearly independence conditions on the activation function and its derivatives, we show that the parameter estimation rates are significantly improved to polynomial rates.

A General Theory for Softmax Gating Multinomial Logistic Mixture of Experts

Mixture-of-experts (MoE) model incorporates the power of multiple submodels via gating functions to achieve greater performance in numerous regression and classification applications. From a theoretical perspective, while there have been previous attempts to comprehend the behavior of that model under the regression settings through the convergence analysis of maximum likelihood estimation in the Gaussian MoE model, such analysis under the setting of a classification problem has remained missing in the literature. We close this gap by establishing the convergence rates of density estimation and parameter estimation in the softmax gating multinomial logistic MoE model. Notably, when part of the expert parameters vanish, these rates are shown to be slower than polynomial rates owing to an inherent interaction between the softmax gating and expert functions via partial differential equations. To address this issue, we propose using a novel class of modified softmax gating functions which transform the input value before delivering them to the gating functions. As a result, the previous interaction disappears and the parameter estimation rates are significantly improved.

Statistical Perspective of Top-K Sparse Softmax Gating Mixture of Experts

Top-K sparse softmax gating mixture of experts has been widely used for scaling up massive deep-learning architectures without increasing the computational cost. Despite its popularity in real-world applications, the theoretical understanding of that gating function has remained an open problem. The main challenge comes from the structure of the top-K sparse softmax gating function, which partitions the input space into multiple regions with distinct behaviors. By focusing on a Gaussian mixture of experts, we establish theoretical results on the effects of the top-K sparse softmax gating function on both density and parameter estimations. Our results hinge upon defining novel loss functions among parameters to capture different behaviors of the input regions. When the true number of experts $k_{\ast}$ is known, we demonstrate that the convergence rates of density and parameter estimations are both parametric on the sample size. However, when $k_{\ast}$ becomes unknown and the true model is over-specified by a Gaussian mixture of $k$ experts where $k > k_{\ast}$, our findings suggest that the number of experts selected from the top-K sparse softmax gating function must exceed the total cardinality of a certain number of Voronoi cells associated with the true parameters to guarantee the convergence of the density estimation. Moreover, while the density estimation rate remains parametric under this setting, the parameter estimation rates become substantially slow due to an intrinsic interaction between the softmax gating and expert functions.