On the Geometry of Separation in Finite Gaussian Mixtures

We study an open problem of understanding the effects of the minimum component separation on the convergence rates of parameter estimation in finite Gaussian mixtures. We address this by developing a unified geometric framework based on novel Hellinger lower bounds that directly relate discrepancies between mixture densities directly to Wasserstein distances between their underlying mixing measures, with explicit dependence on both the minimum separation and the minimum weight. Our approach combines carefully designed interpolation polynomials with confluent divided difference techniques to construct specialized moment-extraction test functions. When the number of components is known, these bounds uncover a localization phenomenon: the separation complexity is driven strictly by the spatial configuration of mixture components, namely, whether they are concentrated in a single cluster, partitioned into multiple clusters separated by a macroscopic gap, or arranged without any structural constraints. On the other hand, when the number of components becomes unknown and is over-specified, the separation complexity is slightly reduced, while the minimum mixture weight disappears entirely from the convergence rates due to a transition from first-order to second-order Wasserstein geometry. As a consequence, we obtain separation-dependent convergence rates that continuously interpolate between point-wise and uniform estimation regimes, thereby settling the fundamental limits of parameter recovery in finite Gaussian mixtures.

The Confidence Trap: Calibration Attacks for Graph Neural Networks

While confidence calibration is essential for trustworthy decision-making in safety-critical applications, the robustness of calibrated GNNs to adversarial structural perturbations remains largely unexplored. However, studying calibration attacks on graphs presents unique technical challenges: (1) the discrete nature of graph structures complicates gradient-based optimization, (2) existing underconfidence objectives fail to drive predictions toward uniform distributions, and (3) GNNs are highly sensitive to edge perturbations, often causing unintended label changes that violate attack constraints. To address these challenges, we propose a \textbf{Unified Graph Calibration Attack (UGCA)} framework designed for \textbf{worst-case (white-box) analysis} of GNN calibration robustness. UGCA introduces a KL-divergence loss to encourage uniform predictive distributions, a reranking mechanism to reduce label flipping, a hybrid loss to recover labels when violations occur, and beam search to explore a broader adversarial search space. We further provide theoretical insights linking model generalization, dataset complexity, and calibration vulnerability, showing that models with higher accuracy or trained on datasets with more classes are more susceptible under this threat model. Extensive experiments demonstrate that UGCA substantially increases Expected Calibration Error while preserving classification accuracy. Our code is publicly available at https://github.com/CaptainCuong/Graph-Calibration-Attack.git.

Improving Minimax Estimation Rates for Contaminated Mixture of Multinomial Logistic Experts via Expert Heterogeneity

Contaminated mixture of experts (MoE) is motivated by transfer learning methods where a pre-trained model, acting as a frozen expert, is integrated with an adapter model, functioning as a trainable expert, in order to learn a new task. Despite recent efforts to analyze the convergence behavior of parameter estimation in this model, there are still two unresolved problems in the literature. First, the contaminated MoE model has been studied solely in regression settings, while its theoretical foundation in classification settings remains absent. Second, previous works on MoE models for classification capture pointwise convergence rates for parameter estimation without any guaranty of minimax optimality. In this work, we close these gaps by performing, for the first time, the convergence analysis of a contaminated mixture of multinomial logistic experts with homogeneous and heterogeneous structures, respectively. In each regime, we characterize uniform convergence rates for estimating parameters under challenging settings where ground-truth parameters vary with the sample size. Furthermore, we also establish corresponding minimax lower bounds to ensure that these rates are minimax optimal. Notably, our theories offer an important insight into the design of contaminated MoE, that is, expert heterogeneity yields faster parameter estimation rates and, therefore, is more sample-efficient than expert homogeneity.

HoRA: Cross-Head Low-Rank Adaptation with Joint Hypernetworks

Low-Rank Adaptation (LoRA) is a parameter-efficient fine-tuning (PEFT) technique that adapts large pre-trained models by adding low-rank matrices to their weight updates. However, in the context of fine-tuning multi-head self-attention (MHA), LoRA has been employed to adapt each attention head separately, thereby overlooking potential synergies across different heads. To mitigate this issue, we propose a novel Hyper-shared Low-Rank Adaptation (HoRA) method, which utilizes joint hypernetworks to generate low-rank matrices across attention heads. By coupling their adaptation through a shared generator, HoRA encourages cross-head information sharing, and thus directly addresses the aforementioned limitation of LoRA. By comparing LoRA and HoRA through the lens of hierarchical mixture of experts, our theoretical findings reveal that the latter achieves superior sample efficiency to the former. Furthermore, through extensive experiments across diverse language and vision benchmarks, we demonstrate that HoRA outperforms LoRA and other PEFT methods while requiring only a marginal increase in the number of trainable parameters.

On Minimax Estimation of Parameters in Softmax-Contaminated Mixture of Experts

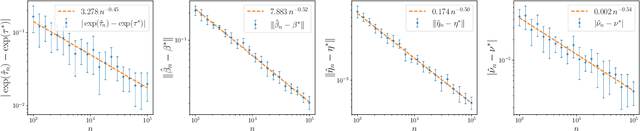
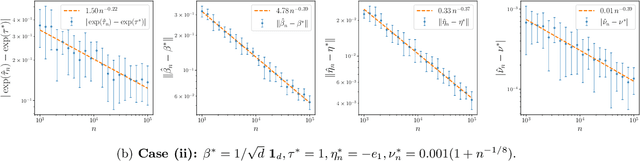
The softmax-contaminated mixture of experts (MoE) model is deployed when a large-scale pre-trained model, which plays the role of a fixed expert, is fine-tuned for learning downstream tasks by including a new contamination part, or prompt, functioning as a new, trainable expert. Despite its popularity and relevance, the theoretical properties of the softmax-contaminated MoE have remained unexplored in the literature. In the paper, we study the convergence rates of the maximum likelihood estimator of gating and prompt parameters in order to gain insights into the statistical properties and potential challenges of fine-tuning with a new prompt. We find that the estimability of these parameters is compromised when the prompt acquires overlapping knowledge with the pre-trained model, in the sense that we make precise by formulating a novel analytic notion of distinguishability. Under distinguishability of the pre-trained and prompt models, we derive minimax optimal estimation rates for all the gating and prompt parameters. By contrast, when the distinguishability condition is violated, these estimation rates become significantly slower due to their dependence on the prompt convergence rate to the pre-trained model. Finally, we empirically corroborate our theoretical findings through several numerical experiments.

Understanding Expert Structures on Minimax Parameter Estimation in Contaminated Mixture of Experts

We conduct the convergence analysis of parameter estimation in the contaminated mixture of experts. This model is motivated from the prompt learning problem where ones utilize prompts, which can be formulated as experts, to fine-tune a large-scaled pre-trained model for learning downstream tasks. There are two fundamental challenges emerging from the analysis: (i) the proportion in the mixture of the pre-trained model and the prompt may converge to zero where the prompt vanishes during the training; (ii) the algebraic interaction among parameters of the pre-trained model and the prompt can occur via some partial differential equation and decelerate the prompt learning. In response, we introduce a distinguishability condition to control the previous parameter interaction. Additionally, we also consider various types of expert structures to understand their effects on the parameter estimation. In each scenario, we provide comprehensive convergence rates of parameter estimation along with the corresponding minimax lower bounds.

On Barycenter Computation: Semi-Unbalanced Optimal Transport-based Method on Gaussians

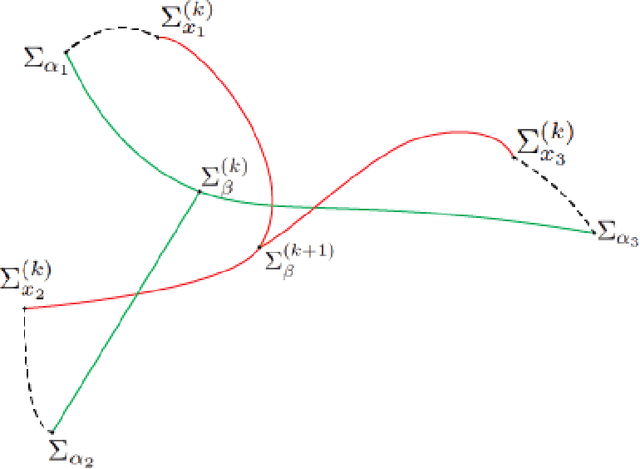
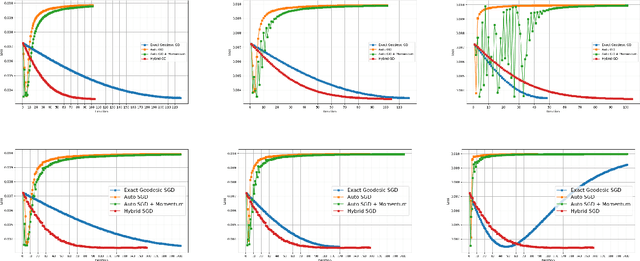
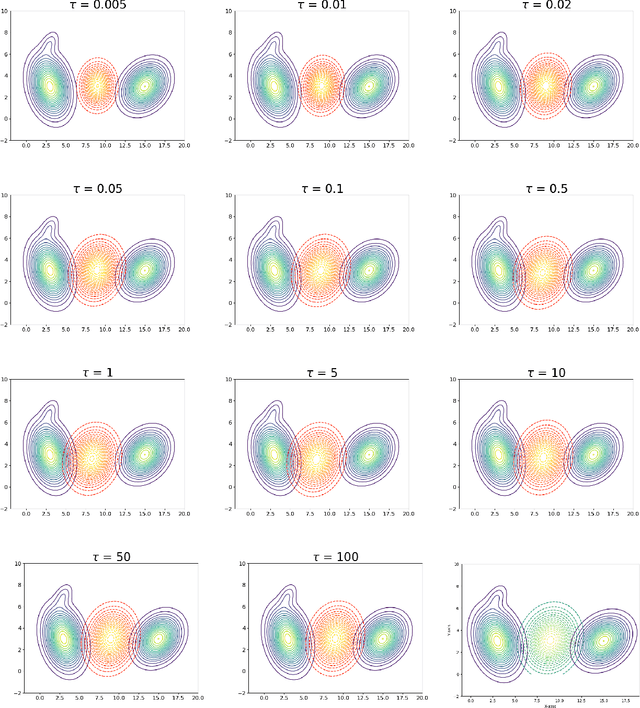
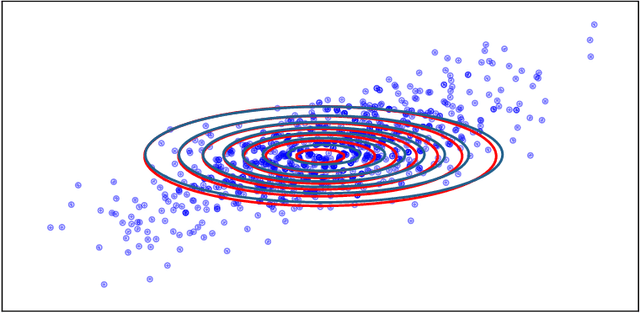
We explore a robust version of the barycenter problem among $n$ centered Gaussian probability measures, termed Semi-Unbalanced Optimal Transport (SUOT)-based Barycenter, wherein the barycenter remains fixed while the others are relaxed using Kullback-Leibler divergence. We develop optimization algorithms on Bures-Wasserstein manifold, named the Exact Geodesic Gradient Descent and Hybrid Gradient Descent algorithms. While the Exact Geodesic Gradient Descent method is based on computing the exact closed form of the first-order derivative of the objective function of the barycenter along a geodesic on the Bures manifold, the Hybrid Gradient Descent method utilizes optimizer components when solving the SUOT problem to replace outlier measures before applying the Riemannian Gradient Descent. We establish the theoretical convergence guarantees for both methods and demonstrate that the Exact Geodesic Gradient Descent algorithm attains a dimension-free convergence rate. Finally, we conduct experiments to compare the normal Wasserstein Barycenter with ours and perform an ablation study.

Fast Approximation of the Generalized Sliced-Wasserstein Distance

Generalized sliced Wasserstein distance is a variant of sliced Wasserstein distance that exploits the power of non-linear projection through a given defining function to better capture the complex structures of the probability distributions. Similar to sliced Wasserstein distance, generalized sliced Wasserstein is defined as an expectation over random projections which can be approximated by the Monte Carlo method. However, the complexity of that approximation can be expensive in high-dimensional settings. To that end, we propose to form deterministic and fast approximations of the generalized sliced Wasserstein distance by using the concentration of random projections when the defining functions are polynomial function, circular function, and neural network type function. Our approximations hinge upon an important result that one-dimensional projections of a high-dimensional random vector are approximately Gaussian.

Transformer with a Mixture of Gaussian Keys

Multi-head attention is a driving force behind state-of-the-art transformers which achieve remarkable performance across a variety of natural language processing (NLP) and computer vision tasks. It has been observed that for many applications, those attention heads learn redundant embedding, and most of them can be removed without degrading the performance of the model. Inspired by this observation, we propose Transformer with a Mixture of Gaussian Keys (Transformer-MGK), a novel transformer architecture that replaces redundant heads in transformers with a mixture of keys at each head. These mixtures of keys follow a Gaussian mixture model and allow each attention head to focus on different parts of the input sequence efficiently. Compared to its conventional transformer counterpart, Transformer-MGK accelerates training and inference, has fewer parameters, and requires less FLOPs to compute while achieving comparable or better accuracy across tasks. Transformer-MGK can also be easily extended to use with linear attentions. We empirically demonstrate the advantage of Transformer-MGK in a range of practical applications including language modeling and tasks that involve very long sequences. On the Wikitext-103 and Long Range Arena benchmark, Transformer-MGKs with 4 heads attain comparable or better performance to the baseline transformers with 8 heads.

Entropic Gromov-Wasserstein between Gaussian Distributions

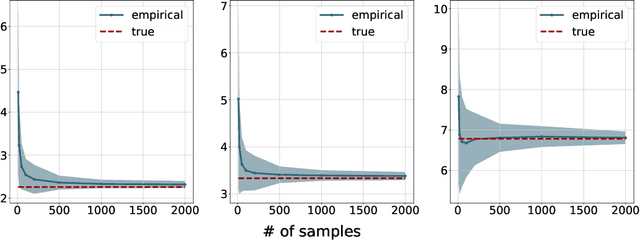
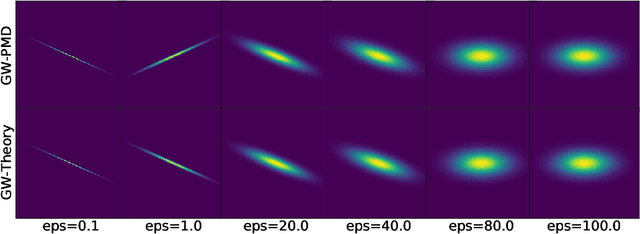
We study the entropic Gromov-Wasserstein and its unbalanced version between (unbalanced) Gaussian distributions with different dimensions. When the metric is the inner product, which we refer to as inner product Gromov-Wasserstein (IGW), we demonstrate that the optimal transportation plans of entropic IGW and its unbalanced variant are (unbalanced) Gaussian distributions. Via an application of von Neumann's trace inequality, we obtain closed-form expressions for the entropic IGW between these Gaussian distributions. Finally, we consider an entropic inner product Gromov-Wasserstein barycenter of multiple Gaussian distributions. We prove that the barycenter is Gaussian distribution when the entropic regularization parameter is small. We further derive closed-form expressions for the covariance matrix of the barycenter.