Entropic Gromov-Wasserstein between Gaussian Distributions

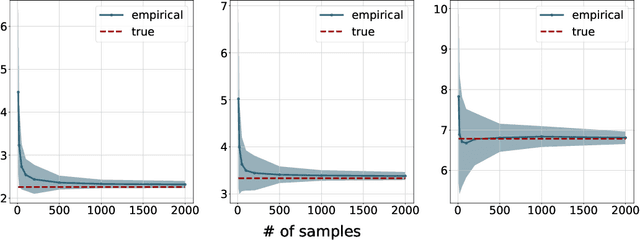
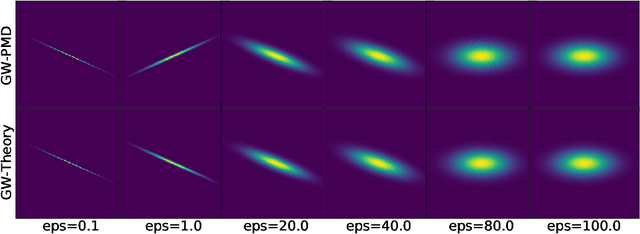
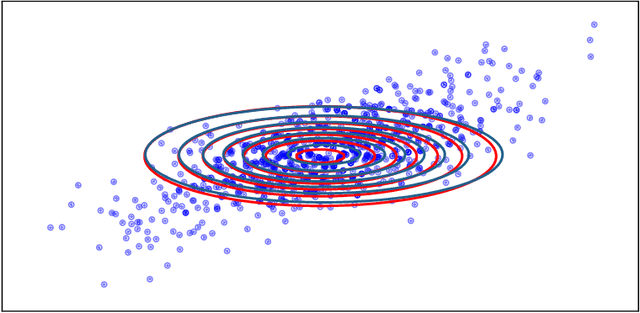
We study the entropic Gromov-Wasserstein and its unbalanced version between (unbalanced) Gaussian distributions with different dimensions. When the metric is the inner product, which we refer to as inner product Gromov-Wasserstein (IGW), we demonstrate that the optimal transportation plans of entropic IGW and its unbalanced variant are (unbalanced) Gaussian distributions. Via an application of von Neumann's trace inequality, we obtain closed-form expressions for the entropic IGW between these Gaussian distributions. Finally, we consider an entropic inner product Gromov-Wasserstein barycenter of multiple Gaussian distributions. We prove that the barycenter is Gaussian distribution when the entropic regularization parameter is small. We further derive closed-form expressions for the covariance matrix of the barycenter.

On Multimarginal Partial Optimal Transport: Equivalent Forms and Computational Complexity

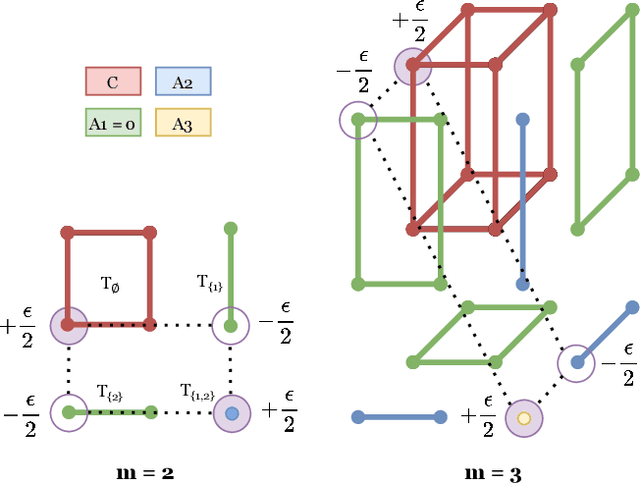
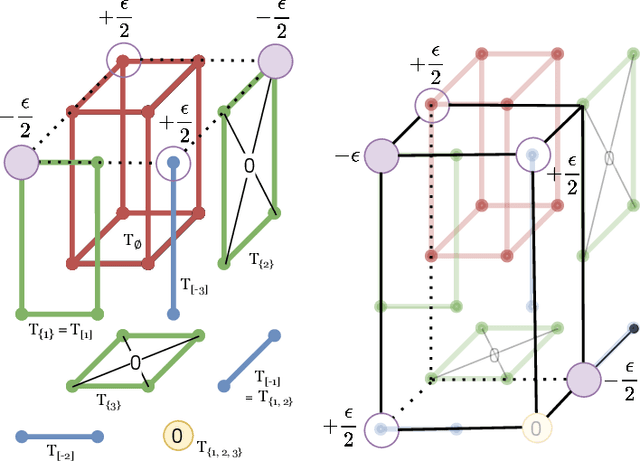
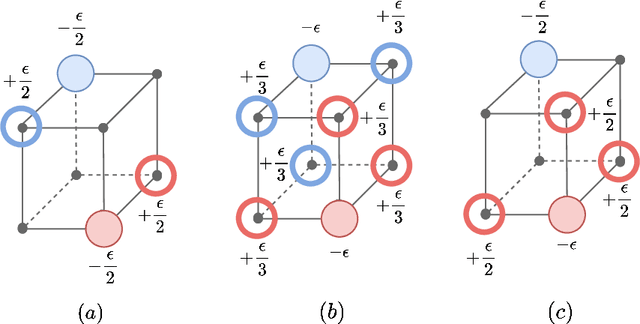
We study the multi-marginal partial optimal transport (POT) problem between $m$ discrete (unbalanced) measures with at most $n$ supports. We first prove that we can obtain two equivalence forms of the multimarginal POT problem in terms of the multimarginal optimal transport problem via novel extensions of cost tensor. The first equivalence form is derived under the assumptions that the total masses of each measure are sufficiently close while the second equivalence form does not require any conditions on these masses but at the price of more sophisticated extended cost tensor. Our proof techniques for obtaining these equivalence forms rely on novel procedures of moving mass in graph theory to push transportation plan into appropriate regions. Finally, based on the equivalence forms, we develop optimization algorithm, named ApproxMPOT algorithm, that builds upon the Sinkhorn algorithm for solving the entropic regularized multimarginal optimal transport. We demonstrate that the ApproxMPOT algorithm can approximate the optimal value of multimarginal POT problem with a computational complexity upper bound of the order $\tilde{\mathcal{O}}(m^3(n+1)^{m}/ \varepsilon^2)$ where $\varepsilon > 0$ stands for the desired tolerance.

On Robust Optimal Transport: Computational Complexity, Low-rank Approximation, and Barycenter Computation

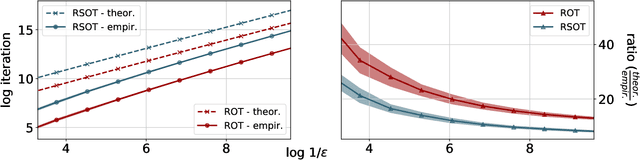
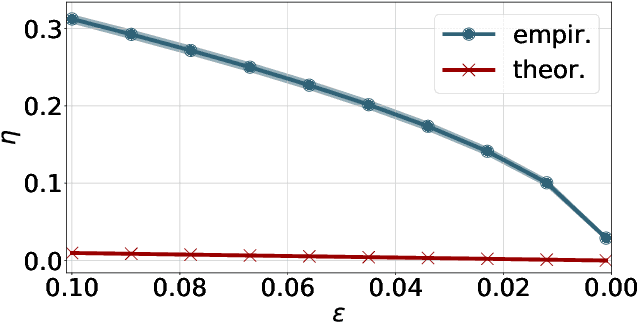
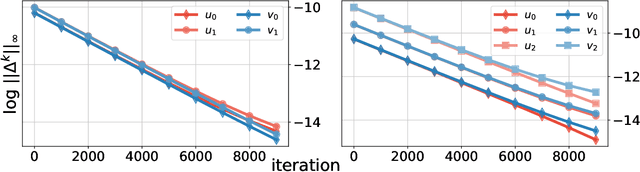
We consider two robust versions of optimal transport, named $\textit{Robust Semi-constrained Optimal Transport}$ (RSOT) and $\textit{Robust Unconstrained Optimal Transport}$ (ROT), formulated by relaxing the marginal constraints with Kullback-Leibler divergence. For both problems in the discrete settings, we propose Sinkhorn-based algorithms that produce $\varepsilon$-approximations of RSOT and ROT in $\widetilde{\mathcal{O}}(\frac{n^2}{\varepsilon})$ time, where $n$ is the number of supports of the probability distributions. Furthermore, to reduce the dependency of the complexity of the Sinkhorn-based algorithms on $n$, we apply Nystr\"{o}m method to approximate the kernel matrix in both RSOT and ROT by a matrix of rank $r$ before passing it to these Sinkhorn-based algorithms. We demonstrate that these new algorithms have $\widetilde{\mathcal{O}}(n r^2 + \frac{nr}{\varepsilon})$ runtime to obtain the RSOT and ROT $\varepsilon$-approximations. Finally, we consider a barycenter problem based on RSOT, named $\textit{Robust Semi-Constrained Barycenter}$ problem (RSBP), and develop a robust iterative Bregman projection algorithm, called $\textbf{Normalized-RobustIBP}$ algorithm, to solve the RSBP in the discrete settings of probability distributions. We show that an $\varepsilon$-approximated solution of the RSBP can be achieved in $\widetilde{\mathcal{O}}(\frac{mn^2}{\varepsilon})$ time using $\textbf{Normalized-RobustIBP}$ algorithm when $m = 2$, which is better than the previous complexity $\widetilde{\mathcal{O}}(\frac{mn^2}{\varepsilon^2})$ of IBP algorithm for approximating the Wasserstein barycenter. Extensive experiments confirm our theoretical results.

On Unbalanced Optimal Transport: An Analysis of Sinkhorn Algorithm

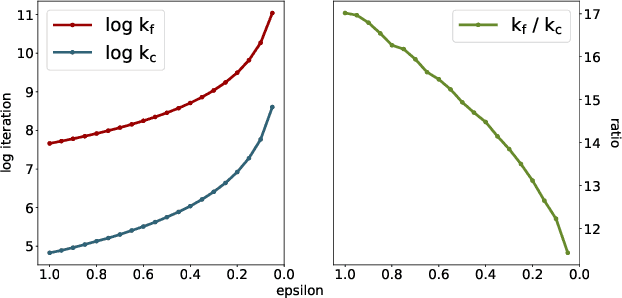
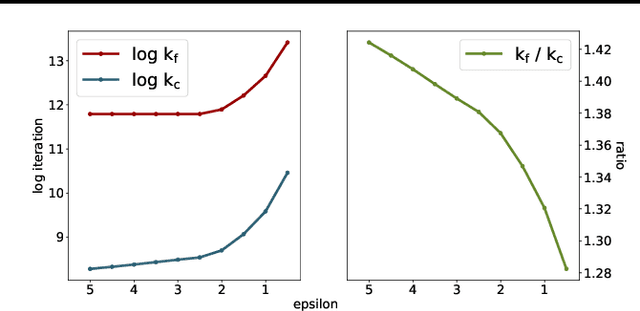
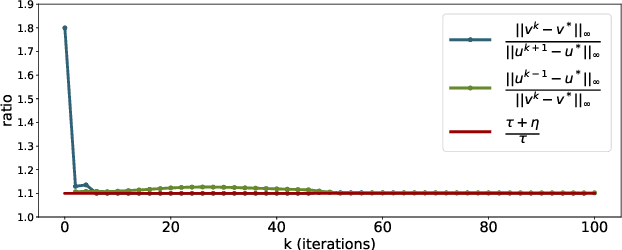
We provide a computational complexity analysis for the Sinkhorn algorithm that solves the entropic regularized Unbalanced Optimal Transport (UOT) problem between two measures of possibly different masses with at most $n$ components. We show that the complexity of the Sinkhorn algorithm for finding an $\varepsilon$-approximate solution to the UOT problem is of order $\widetilde{\mathcal{O}}(n^2/ \varepsilon)$, which is near-linear time. To the best of our knowledge, this complexity is better than the complexity of the Sinkhorn algorithm for solving the Optimal Transport (OT) problem, which is of order $\widetilde{\mathcal{O}}(n^2/\varepsilon^2)$. Our proof technique is based on the geometric convergence of the Sinkhorn updates to the optimal dual solution of the entropic regularized UOT problem and some properties of the primal solution. It is also different from the proof for the complexity of the Sinkhorn algorithm for approximating the OT problem since the UOT solution does not have to meet the marginal constraints.