Stable Estimation of Survival Causal Effects

We study the problem of estimating survival causal effects, where the aim is to characterize the impact of an intervention on survival times, i.e., how long it takes for an event to occur. Applications include determining if a drug reduces the time to ICU discharge or if an advertising campaign increases customer dwell time. Historically, the most popular estimates have been based on parametric or semiparametric (e.g. proportional hazards) models; however, these methods suffer from problematic levels of bias. Recently debiased machine learning approaches are becoming increasingly popular, especially in applications to large datasets. However, despite their appealing theoretical properties, these estimators tend to be unstable because the debiasing step involves the use of the inverses of small estimated probabilities -- small errors in the estimated probabilities can result in huge changes in their inverses and therefore the resulting estimator. This problem is exacerbated in survival settings where probabilities are a product of treatment assignment and censoring probabilities. We propose a covariate balancing approach to estimating these inverses directly, sidestepping this problem. The result is an estimator that is stable in practice and enjoys many of the same theoretical properties. In particular, under overlap and asymptotic equicontinuity conditions, our estimator is asymptotically normal with negligible bias and optimal variance. Our experiments on synthetic and semi-synthetic data demonstrate that our method has competitive bias and smaller variance than debiased machine learning approaches.

Scale up with Order: Finding Good Data Permutations for Distributed Training

Gradient Balancing (GraB) is a recently proposed technique that finds provably better data permutations when training models with multiple epochs over a finite dataset. It converges at a faster rate than the widely adopted Random Reshuffling, by minimizing the discrepancy of the gradients on adjacently selected examples. However, GraB only operates under critical assumptions such as small batch sizes and centralized data, leaving open the question of how to order examples at large scale -- i.e. distributed learning with decentralized data. To alleviate the limitation, in this paper we propose D-GraB that involves two novel designs: (1) $\textsf{PairBalance}$ that eliminates the requirement to use stale gradient mean in GraB which critically relies on small learning rates; (2) an ordering protocol that runs $\textsf{PairBalance}$ in a distributed environment with negligible overhead, which benefits from both data ordering and parallelism. We prove D-GraB enjoys linear speed up at rate $\tilde{O}((mnT)^{-2/3})$ on smooth non-convex objectives and $\tilde{O}((mnT)^{-2})$ under PL condition, where $n$ denotes the number of parallel workers, $m$ denotes the number of examples per worker and $T$ denotes the number of epochs. Empirically, we show on various applications including GLUE, CIFAR10 and WikiText-2 that D-GraB outperforms naive parallel GraB and Distributed Random Reshuffling in terms of both training and validation performance.

Combining GHOST and Casper

We present "Gasper," a proof-of-stake-based consensus protocol, which is an idealized version of the proposed Ethereum 2.0 beacon chain. The protocol combines Casper FFG, a finality tool, with LMD GHOST, a fork-choice rule. We prove safety, plausible liveness, and probabilistic liveness under different sets of assumptions.

On Unbalanced Optimal Transport: An Analysis of Sinkhorn Algorithm

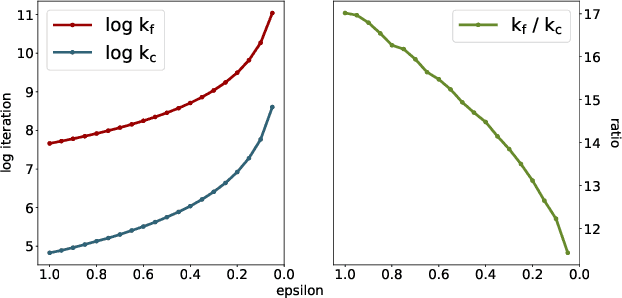
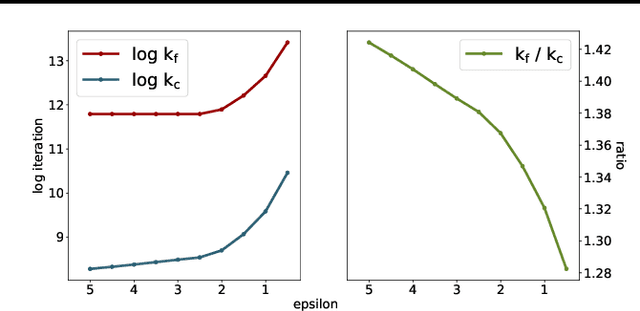
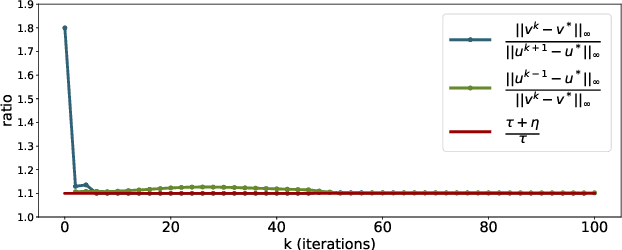
We provide a computational complexity analysis for the Sinkhorn algorithm that solves the entropic regularized Unbalanced Optimal Transport (UOT) problem between two measures of possibly different masses with at most $n$ components. We show that the complexity of the Sinkhorn algorithm for finding an $\varepsilon$-approximate solution to the UOT problem is of order $\widetilde{\mathcal{O}}(n^2/ \varepsilon)$, which is near-linear time. To the best of our knowledge, this complexity is better than the complexity of the Sinkhorn algorithm for solving the Optimal Transport (OT) problem, which is of order $\widetilde{\mathcal{O}}(n^2/\varepsilon^2)$. Our proof technique is based on the geometric convergence of the Sinkhorn updates to the optimal dual solution of the entropic regularized UOT problem and some properties of the primal solution. It is also different from the proof for the complexity of the Sinkhorn algorithm for approximating the OT problem since the UOT solution does not have to meet the marginal constraints.

Evaluating Syntactic Properties of Seq2seq Output with a Broad Coverage HPSG: A Case Study on Machine Translation

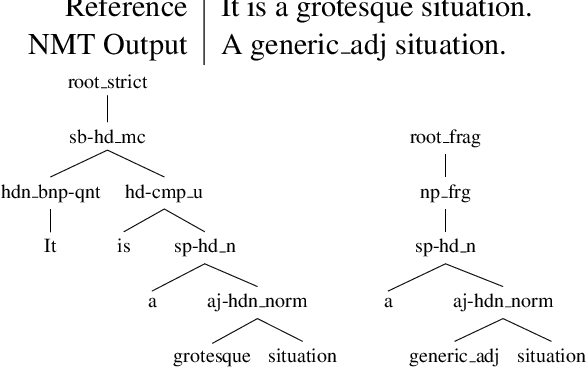
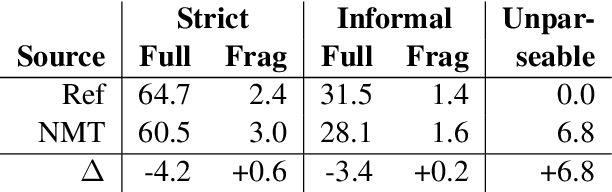
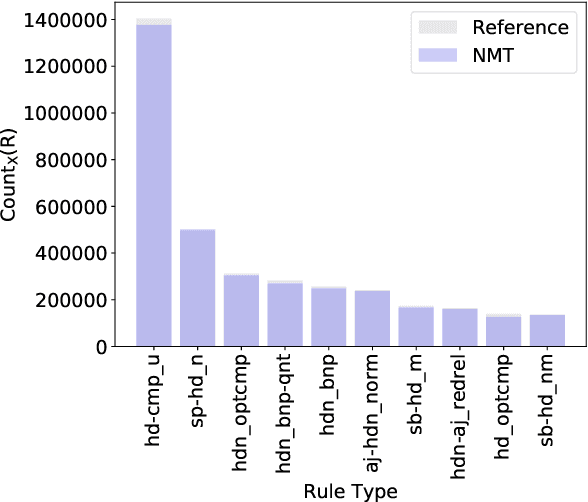
Sequence to sequence (seq2seq) models are often employed in settings where the target output is natural language. However, the syntactic properties of the language generated from these models are not well understood. We explore whether such output belongs to a formal and realistic grammar, by employing the English Resource Grammar (ERG), a broad coverage, linguistically precise HPSG-based grammar of English. From a French to English parallel corpus, we analyze the parseability and grammatical constructions occurring in output from a seq2seq translation model. Over 93\% of the model translations are parseable, suggesting that it learns to generate conforming to a grammar. The model has trouble learning the distribution of rarer syntactic rules, and we pinpoint several constructions that differentiate translations between the references and our model.