Non-parametric efficient estimation of marginal structural models with multi-valued time-varying treatments

Marginal structural models are a popular method for estimating causal effects in the presence of time-varying exposures. In spite of their popularity, no scalable non-parametric estimator exist for marginal structural models with multi-valued and time-varying treatments. In this paper, we use machine learning together with recent developments in semiparametric efficiency theory for longitudinal studies to propose such an estimator. The proposed estimator is based on a study of the non-parametric identifying functional, including first order von-Mises expansions as well as the efficient influence function and the efficiency bound. We show conditions under which the proposed estimator is efficient, asymptotically normal, and sequentially doubly robust in the sense that it is consistent if, for each time point, either the outcome or the treatment mechanism is consistently estimated. We perform a simulation study to illustrate the properties of the estimators, and present the results of our motivating study on a COVID-19 dataset studying the impact of mobility on the cumulative number of observed cases.

Chimera: Effectively Modeling Multivariate Time Series with 2-Dimensional State Space Models

Modeling multivariate time series is a well-established problem with a wide range of applications from healthcare to financial markets. Traditional State Space Models (SSMs) are classical approaches for univariate time series modeling due to their simplicity and expressive power to represent linear dependencies. They, however, have fundamentally limited expressive power to capture non-linear dependencies, are slow in practice, and fail to model the inter-variate information flow. Despite recent attempts to improve the expressive power of SSMs by using deep structured SSMs, the existing methods are either limited to univariate time series, fail to model complex patterns (e.g., seasonal patterns), fail to dynamically model the dependencies of variate and time dimensions, and/or are input-independent. We present Chimera that uses two input-dependent 2-D SSM heads with different discretization processes to learn long-term progression and seasonal patterns. To improve the efficiency of complex 2D recurrence, we present a fast training using a new 2-dimensional parallel selective scan. We further present and discuss 2-dimensional Mamba and Mamba-2 as the spacial cases of our 2D SSM. Our experimental evaluation shows the superior performance of Chimera on extensive and diverse benchmarks, including ECG and speech time series classification, long-term and short-term time series forecasting, and time series anomaly detection.

MambaMixer: Efficient Selective State Space Models with Dual Token and Channel Selection

Recent advances in deep learning have mainly relied on Transformers due to their data dependency and ability to learn at scale. The attention module in these architectures, however, exhibits quadratic time and space in input size, limiting their scalability for long-sequence modeling. Despite recent attempts to design efficient and effective architecture backbone for multi-dimensional data, such as images and multivariate time series, existing models are either data independent, or fail to allow inter- and intra-dimension communication. Recently, State Space Models (SSMs), and more specifically Selective State Space Models, with efficient hardware-aware implementation, have shown promising potential for long sequence modeling. Motivated by the success of SSMs, we present MambaMixer, a new architecture with data-dependent weights that uses a dual selection mechanism across tokens and channels, called Selective Token and Channel Mixer. MambaMixer connects selective mixers using a weighted averaging mechanism, allowing layers to have direct access to early features. As a proof of concept, we design Vision MambaMixer (ViM2) and Time Series MambaMixer (TSM2) architectures based on the MambaMixer block and explore their performance in various vision and time series forecasting tasks. Our results underline the importance of selective mixing across both tokens and channels. In ImageNet classification, object detection, and semantic segmentation tasks, ViM2 achieves competitive performance with well-established vision models and outperforms SSM-based vision models. In time series forecasting, TSM2 achieves outstanding performance compared to state-of-the-art methods while demonstrating significantly improved computational cost. These results show that while Transformers, cross-channel attention, and MLPs are sufficient for good performance in time series forecasting, neither is necessary.

Stable Estimation of Survival Causal Effects

We study the problem of estimating survival causal effects, where the aim is to characterize the impact of an intervention on survival times, i.e., how long it takes for an event to occur. Applications include determining if a drug reduces the time to ICU discharge or if an advertising campaign increases customer dwell time. Historically, the most popular estimates have been based on parametric or semiparametric (e.g. proportional hazards) models; however, these methods suffer from problematic levels of bias. Recently debiased machine learning approaches are becoming increasingly popular, especially in applications to large datasets. However, despite their appealing theoretical properties, these estimators tend to be unstable because the debiasing step involves the use of the inverses of small estimated probabilities -- small errors in the estimated probabilities can result in huge changes in their inverses and therefore the resulting estimator. This problem is exacerbated in survival settings where probabilities are a product of treatment assignment and censoring probabilities. We propose a covariate balancing approach to estimating these inverses directly, sidestepping this problem. The result is an estimator that is stable in practice and enjoys many of the same theoretical properties. In particular, under overlap and asymptotic equicontinuity conditions, our estimator is asymptotically normal with negligible bias and optimal variance. Our experiments on synthetic and semi-synthetic data demonstrate that our method has competitive bias and smaller variance than debiased machine learning approaches.

A Fast Bootstrap Algorithm for Causal Inference with Large Data

Estimating causal effects from large experimental and observational data has become increasingly prevalent in both industry and research. The bootstrap is an intuitive and powerful technique used to construct standard errors and confidence intervals of estimators. Its application however can be prohibitively demanding in settings involving large data. In addition, modern causal inference estimators based on machine learning and optimization techniques exacerbate the computational burden of the bootstrap. The bag of little bootstraps has been proposed in non-causal settings for large data but has not yet been applied to evaluate the properties of estimators of causal effects. In this paper, we introduce a new bootstrap algorithm called causal bag of little bootstraps for causal inference with large data. The new algorithm significantly improves the computational efficiency of the traditional bootstrap while providing consistent estimates and desirable confidence interval coverage. We describe its properties, provide practical considerations, and evaluate the performance of the proposed algorithm in terms of bias, coverage of the true 95% confidence intervals, and computational time in a simulation study. We apply it in the evaluation of the effect of hormone therapy on the average time to coronary heart disease using a large observational data set from the Women's Health Initiative.

Deep survival analysis with longitudinal X-rays for COVID-19

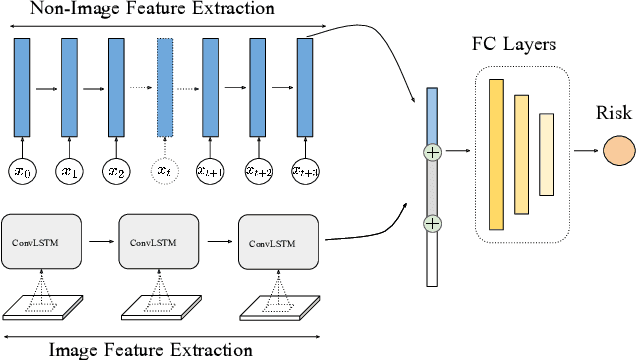
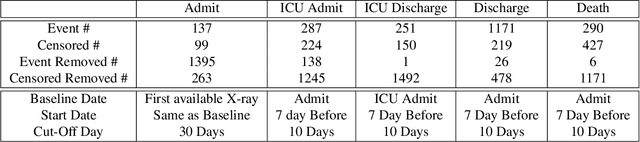
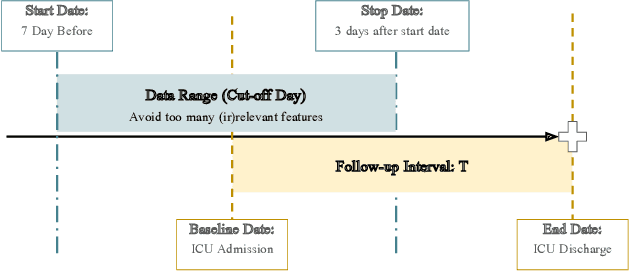
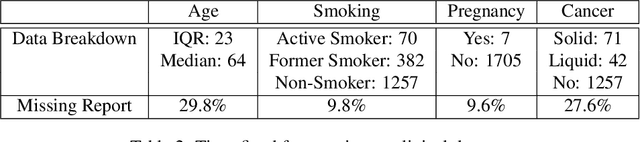
Time-to-event analysis is an important statistical tool for allocating clinical resources such as ICU beds. However, classical techniques like the Cox model cannot directly incorporate images due to their high dimensionality. We propose a deep learning approach that naturally incorporates multiple, time-dependent imaging studies as well as non-imaging data into time-to-event analysis. Our techniques are benchmarked on a clinical dataset of 1,894 COVID-19 patients, and show that image sequences significantly improve predictions. For example, classical time-to-event methods produce a concordance error of around 30-40% for predicting hospital admission, while our error is 25% without images and 20% with multiple X-rays included. Ablation studies suggest that our models are not learning spurious features such as scanner artifacts. While our focus and evaluation is on COVID-19, the methods we develop are broadly applicable.

Kernel Optimal Orthogonality Weighting: A Balancing Approach to Estimating Effects of Continuous Treatments

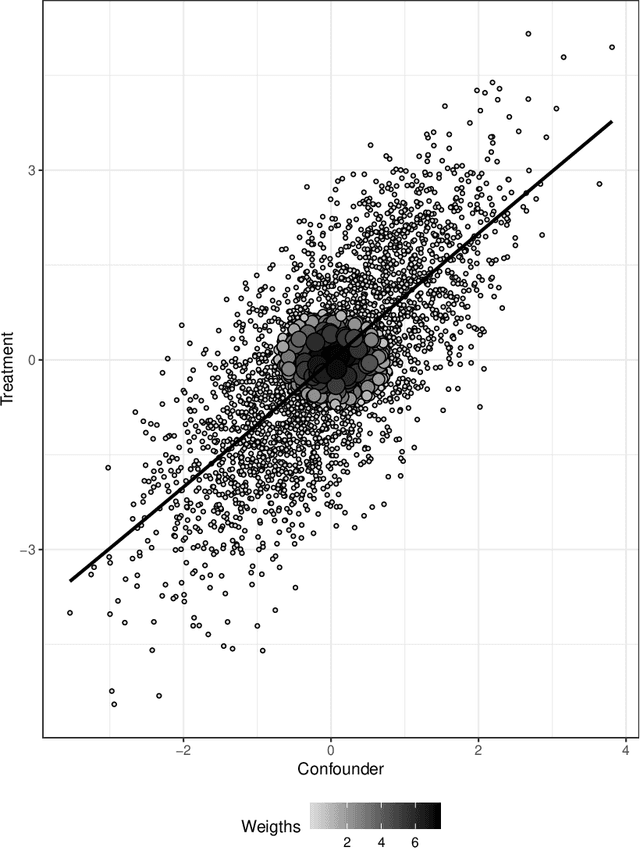
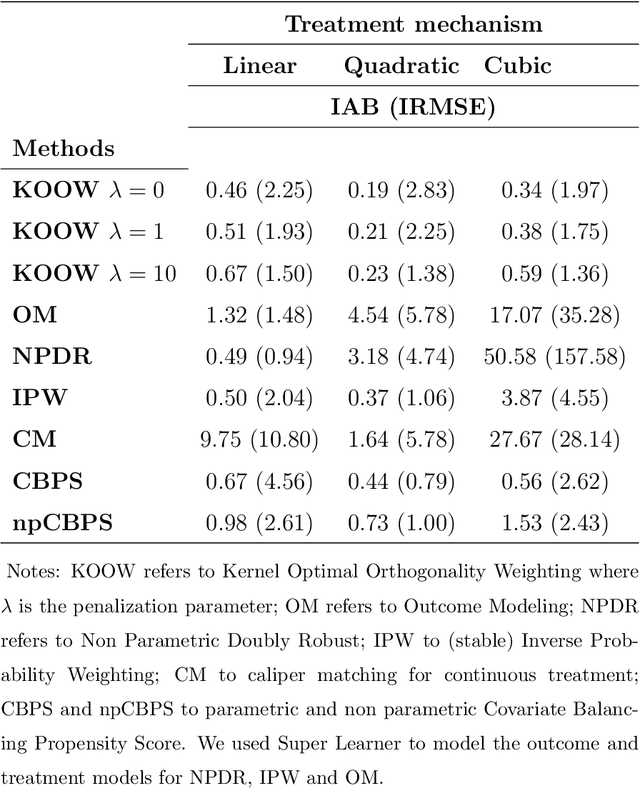
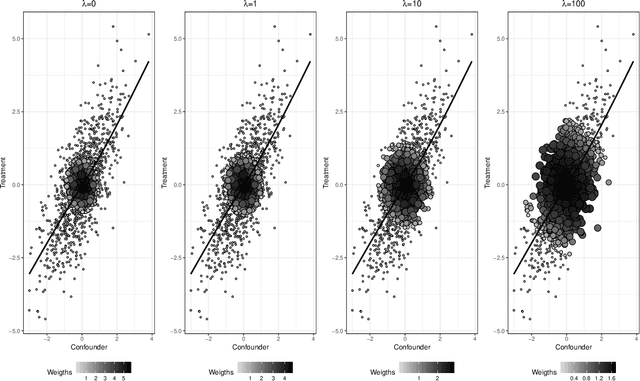
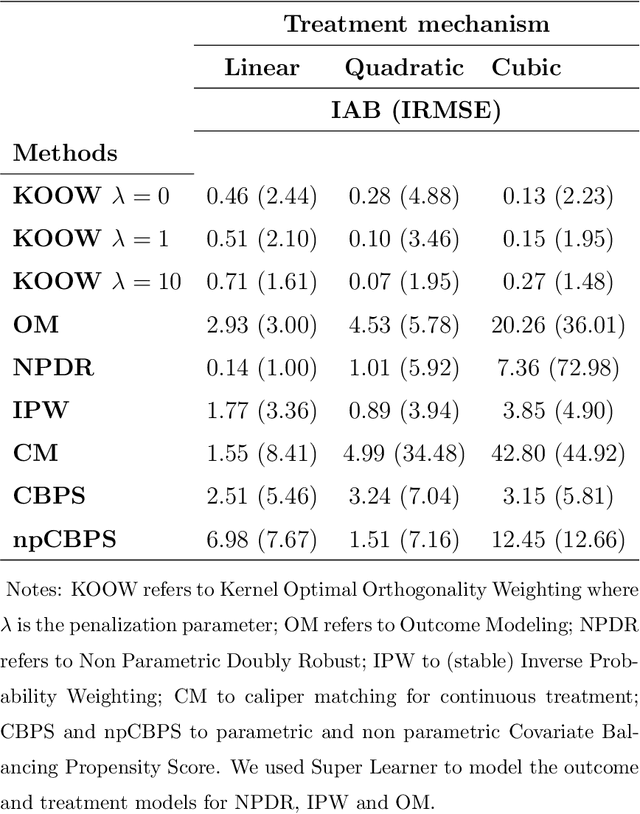
Many scientific questions require estimating the effects of continuous treatments. Outcome modeling and weighted regression based on the generalized propensity score are the most commonly used methods to evaluate continuous effects. However, these techniques may be sensitive to model misspecification, extreme weights or both. In this paper, we propose Kernel Optimal Orthogonality Weighting (KOOW), a convex optimization-based method, for estimating the effects of continuous treatments. KOOW finds weights that minimize the worst-case penalized functional covariance between the continuous treatment and the confounders. By minimizing this quantity, KOOW successfully provides weights that orthogonalize confounders and the continuous treatment, thus providing optimal covariate balance, while controlling for extreme weights. We valuate its comparative performance in a simulation study. Using data from the Women's Health Initiative observational study, we apply KOOW to evaluate the effect of red meat consumption on blood pressure.

Optimal Estimation of Generalized Average Treatment Effects using Kernel Optimal Matching

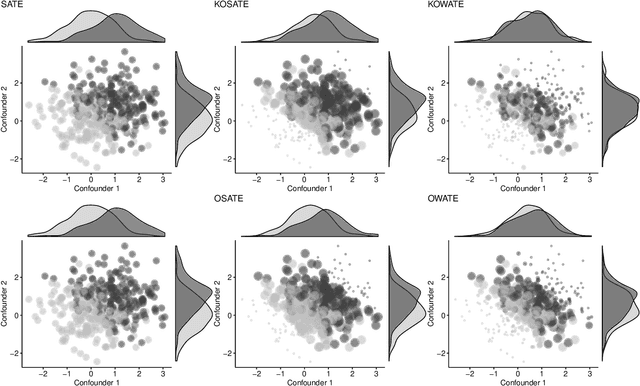
In causal inference, a variety of causal effect estimands have been studied, including the sample, uncensored, target, conditional, optimal subpopulation, and optimal weighted average treatment effects. Ad-hoc methods have been developed for each estimand based on inverse probability weighting (IPW) and on outcome regression modeling, but these may be sensitive to model misspecification, practical violations of positivity, or both. The contribution of this paper is twofold. First, we formulate the generalized average treatment effect (GATE) to unify these causal estimands as well as their IPW estimates. Second, we develop a method based on Kernel Optimal Matching (KOM) to optimally estimate GATE and to find the GATE most easily estimable by KOM, which we term the Kernel Optimal Weighted Average Treatment Effect. KOM provides uniform control on the conditional mean squared error of a weighted estimator over a class of models while simultaneously controlling for precision. We study its theoretical properties and evaluate its comparative performance in a simulation study. We illustrate the use of KOM for GATE estimation in two case studies: comparing spine surgical interventions and studying the effect of peer support on people living with HIV.

CAB: Continuous Adaptive Blending Estimator for Policy Evaluation and Learning

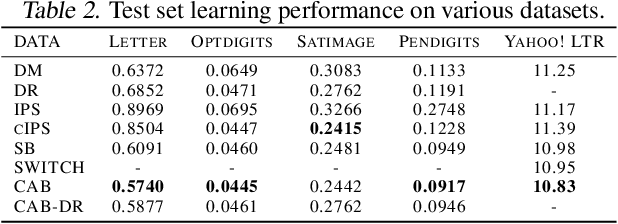
The ability to perform offline A/B-testing and off-policy learning using logged contextual bandit feedback is highly desirable in a broad range of applications, including recommender systems, search engines, ad placement, and personalized health care. Both offline A/B-testing and off-policy learning require a counterfactual estimator that evaluates how some new policy would have performed, if it had been used instead of the logging policy. This paper proposes a new counterfactual estimator - called Continuous Adaptive Blending (CAB) - for this policy evaluation problem that combines regression and weighting approaches for an effective bias/variance trade-off. It can be substantially less biased than clipped Inverse Propensity Score weighting and the Direct Method, and it can have less variance compared with Doubly Robust and IPS estimators. Experimental results show that CAB provides excellent and reliable estimation accuracy compared to other blended estimators, and - unlike the SWITCH estimator - is sub-differentiable such that it can be used for learning.

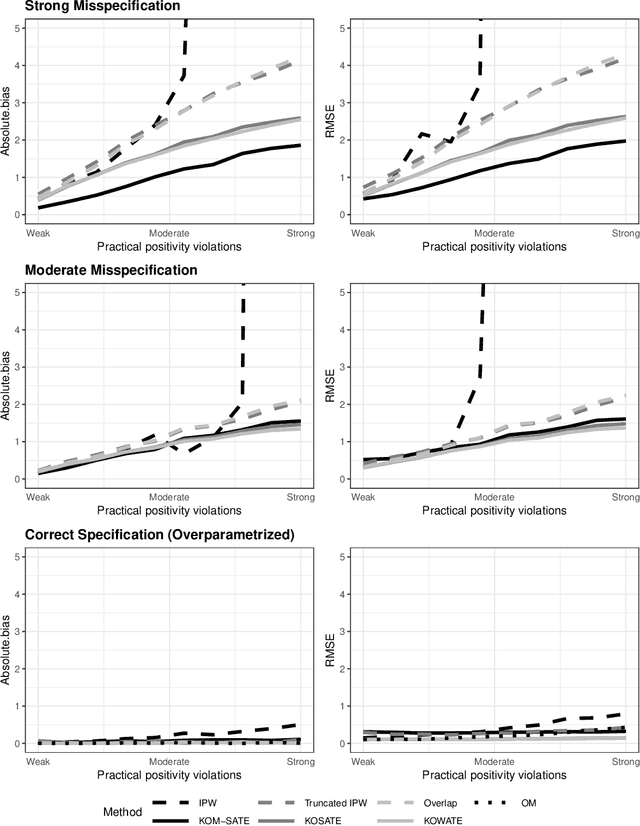
Optimal Balancing of Time-Dependent Confounders for Marginal Structural Models

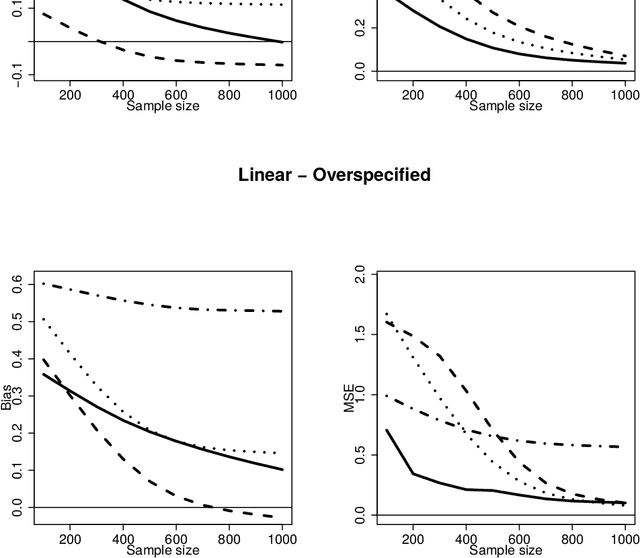
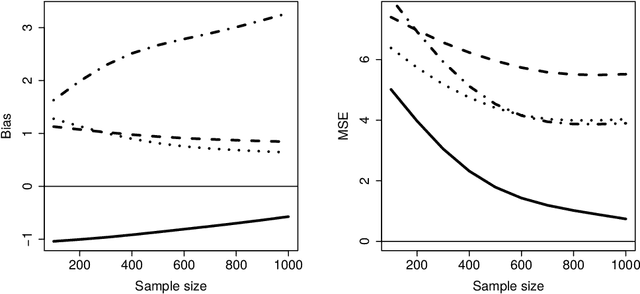
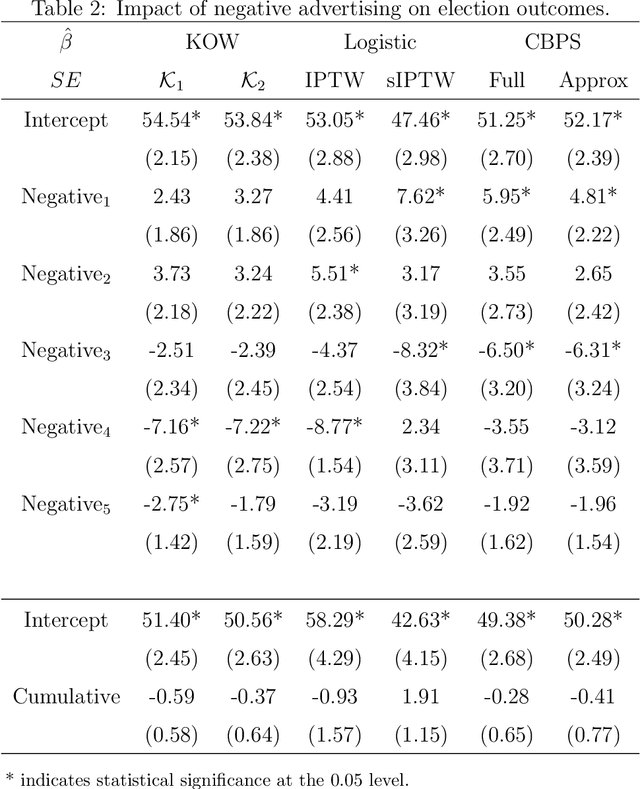
Marginal structural models (MSMs) estimate the causal effect of a time-varying treatment in the presence of time-dependent confounding via weighted regression. The standard approach of using inverse probability of treatment weighting (IPTW) can lead to high-variance estimates due to extreme weights and be sensitive to model misspecification. Various methods have been proposed to partially address this, including truncation and stabilized-IPTW to temper extreme weights and covariate balancing propensity score (CBPS) to address treatment model misspecification. In this paper, we present Kernel Optimal Weighting (KOW), a convex-optimization-based approach that finds weights for fitting the MSM that optimally balance time-dependent confounders while simultaneously controlling for precision, directly addressing the above limitations. KOW directly minimizes the error in estimation due to time-dependent confounding via a new decomposition as a functional. We further extend KOW to control for informative censoring. We evaluate the performance of KOW in a simulation study, comparing it with IPTW, stabilized-IPTW, and CBPS. We demonstrate the use of KOW in studying the effect of treatment initiation on time-to-death among people living with HIV and the effect of negative advertising on elections in the United States.