Stable Estimation of Survival Causal Effects

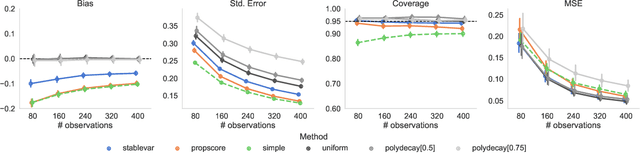
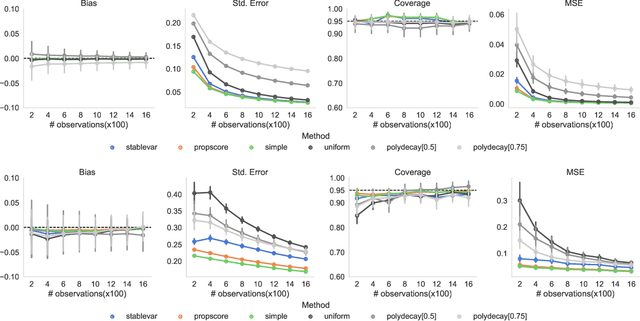
We study the problem of estimating survival causal effects, where the aim is to characterize the impact of an intervention on survival times, i.e., how long it takes for an event to occur. Applications include determining if a drug reduces the time to ICU discharge or if an advertising campaign increases customer dwell time. Historically, the most popular estimates have been based on parametric or semiparametric (e.g. proportional hazards) models; however, these methods suffer from problematic levels of bias. Recently debiased machine learning approaches are becoming increasingly popular, especially in applications to large datasets. However, despite their appealing theoretical properties, these estimators tend to be unstable because the debiasing step involves the use of the inverses of small estimated probabilities -- small errors in the estimated probabilities can result in huge changes in their inverses and therefore the resulting estimator. This problem is exacerbated in survival settings where probabilities are a product of treatment assignment and censoring probabilities. We propose a covariate balancing approach to estimating these inverses directly, sidestepping this problem. The result is an estimator that is stable in practice and enjoys many of the same theoretical properties. In particular, under overlap and asymptotic equicontinuity conditions, our estimator is asymptotically normal with negligible bias and optimal variance. Our experiments on synthetic and semi-synthetic data demonstrate that our method has competitive bias and smaller variance than debiased machine learning approaches.

Off-Policy Evaluation via Adaptive Weighting with Data from Contextual Bandits

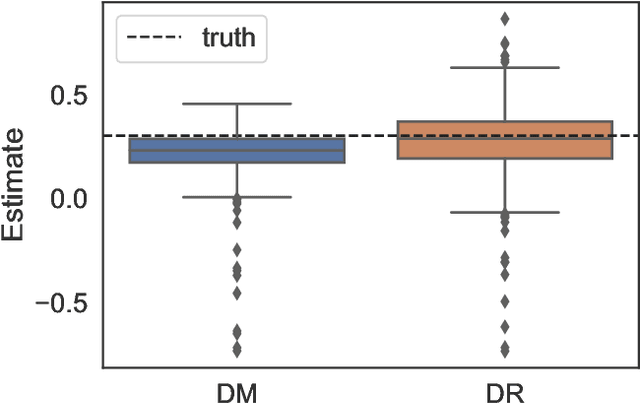
It has become increasingly common for data to be collected adaptively, for example using contextual bandits. Historical data of this type can be used to evaluate other treatment assignment policies to guide future innovation or experiments. However, policy evaluation is challenging if the target policy differs from the one used to collect data, and popular estimators, including doubly robust (DR) estimators, can be plagued by bias, excessive variance, or both. In particular, when the pattern of treatment assignment in the collected data looks little like the pattern generated by the policy to be evaluated, the importance weights used in DR estimators explode, leading to excessive variance. In this paper, we improve the DR estimator by adaptively weighting observations to control its variance. We show that a t-statistic based on our improved estimator is asymptotically normal under certain conditions, allowing us to form confidence intervals and test hypotheses. Using synthetic data and public benchmarks, we provide empirical evidence for our estimator's improved accuracy and inferential properties relative to existing alternatives.

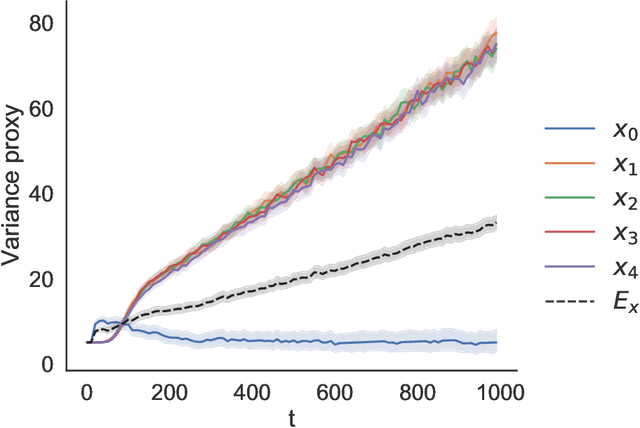
Confidence Intervals for Policy Evaluation in Adaptive Experiments

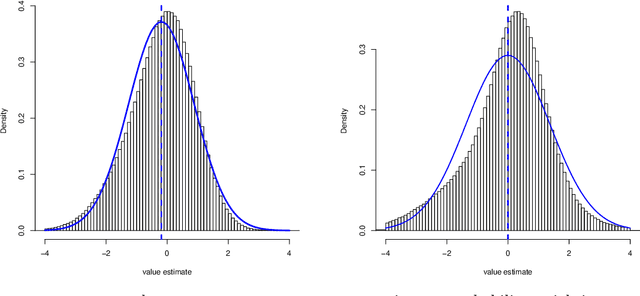
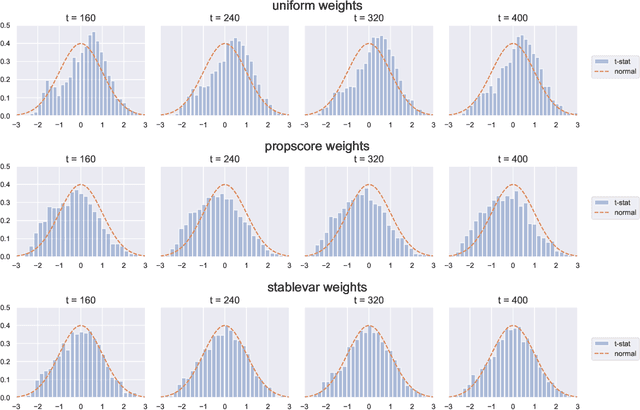
Adaptive experiments can result in considerable cost savings in multi-armed trials by enabling analysts to quickly focus on the most promising alternatives. Most existing work on adaptive experiments (which include multi-armed bandits) has focused maximizing the speed at which the analyst can identify the optimal arm and/or minimizing the number of draws from sub-optimal arms. In many scientific settings, however, it is not only of interest to identify the optimal arm, but also to perform a statistical analysis of the data collected from the experiment. Naive approaches to statistical inference with adaptive inference fail because many commonly used statistics (such as sample means or inverse propensity weighting) do not have an asymptotically Gaussian limiting distribution centered on the estimate, and so confidence intervals constructed from these statistics do not have correct coverage. But, as shown in this paper, carefully designed data-adaptive weighting schemes can be used to overcome this issue and restore a relevant central limit theorem, enabling hypothesis testing. We validate the accuracy of the resulting confidence intervals in numerical experiments.