Contextual Bandits in a Survey Experiment on Charitable Giving: Within-Experiment Outcomes versus Policy Learning

We design and implement an adaptive experiment (a ``contextual bandit'') to learn a targeted treatment assignment policy, where the goal is to use a participant's survey responses to determine which charity to expose them to in a donation solicitation. The design balances two competing objectives: optimizing the outcomes for the subjects in the experiment (``cumulative regret minimization'') and gathering data that will be most useful for policy learning, that is, for learning an assignment rule that will maximize welfare if used after the experiment (``simple regret minimization''). We evaluate alternative experimental designs by collecting pilot data and then conducting a simulation study. Next, we implement our selected algorithm. Finally, we perform a second simulation study anchored to the collected data that evaluates the benefits of the algorithm we chose. Our first result is that the value of a learned policy in this setting is higher when data is collected via a uniform randomization rather than collected adaptively using standard cumulative regret minimization or policy learning algorithms. We propose a simple heuristic for adaptive experimentation that improves upon uniform randomization from the perspective of policy learning at the expense of increasing cumulative regret relative to alternative bandit algorithms. The heuristic modifies an existing contextual bandit algorithm by (i) imposing a lower bound on assignment probabilities that decay slowly so that no arm is discarded too quickly, and (ii) after adaptively collecting data, restricting policy learning to select from arms where sufficient data has been gathered.

Off-Policy Evaluation via Adaptive Weighting with Data from Contextual Bandits

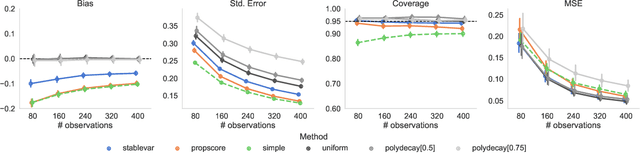
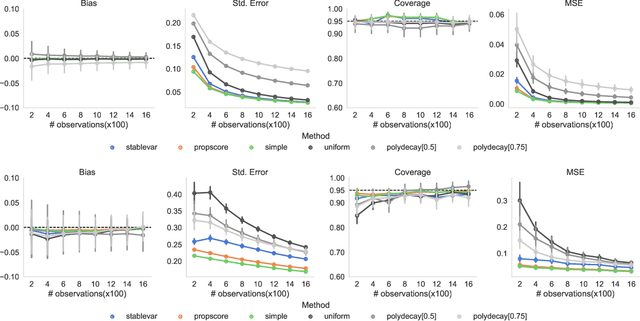
It has become increasingly common for data to be collected adaptively, for example using contextual bandits. Historical data of this type can be used to evaluate other treatment assignment policies to guide future innovation or experiments. However, policy evaluation is challenging if the target policy differs from the one used to collect data, and popular estimators, including doubly robust (DR) estimators, can be plagued by bias, excessive variance, or both. In particular, when the pattern of treatment assignment in the collected data looks little like the pattern generated by the policy to be evaluated, the importance weights used in DR estimators explode, leading to excessive variance. In this paper, we improve the DR estimator by adaptively weighting observations to control its variance. We show that a t-statistic based on our improved estimator is asymptotically normal under certain conditions, allowing us to form confidence intervals and test hypotheses. Using synthetic data and public benchmarks, we provide empirical evidence for our estimator's improved accuracy and inferential properties relative to existing alternatives.

Adapting to misspecification in contextual bandits with offline regression oracles

Computationally efficient contextual bandits are often based on estimating a predictive model of rewards given contexts and arms using past data. However, when the reward model is not well-specified, the bandit algorithm may incur unexpected regret, so recent work has focused on algorithms that are robust to misspecification. We propose a simple family of contextual bandit algorithms that adapt to misspecification error by reverting to a good safe policy when there is evidence that misspecification is causing a regret increase. Our algorithm requires only an offline regression oracle to ensure regret guarantees that gracefully degrade in terms of a measure of the average misspecification level. Compared to prior work, we attain similar regret guarantees, but we do no rely on a master algorithm, and do not require more robust oracles like online or constrained regression oracles (e.g., Foster et al. (2020a); Krishnamurthy et al. (2020)). This allows us to design algorithms for more general function approximation classes.

Tractable contextual bandits beyond realizability

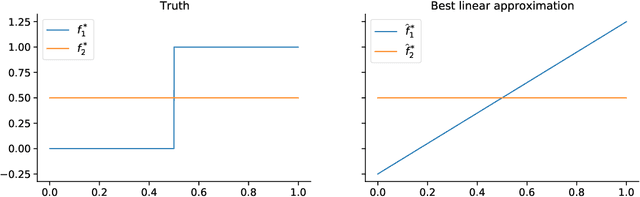
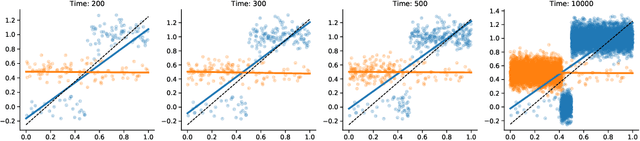
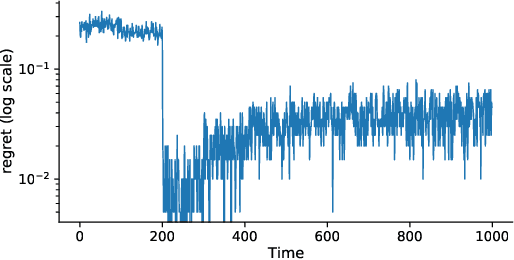
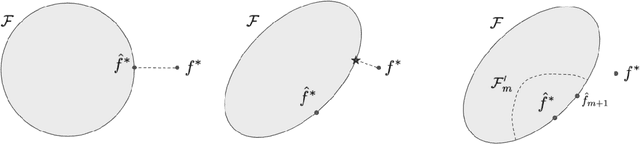
Tractable contextual bandit algorithms often rely on the realizability assumption -- i.e., that the true expected reward model belongs to a known class, such as linear functions. We investigate issues that arise in the absence of realizability and note that the dynamics of adaptive data collection can lead commonly used bandit algorithms to learn a suboptimal policy. In this work, we present a tractable bandit algorithm that is not sensitive to the realizability assumption and computationally reduces to solving a constrained regression problem in every epoch. When realizability does not hold, our algorithm ensures the same guarantees on regret achieved by realizability-based algorithms under realizability, up to an additive term that accounts for the misspecification error. This extra term is proportional to T times the (2/5)-root of the mean squared error between the best model in the class and the true model, where T is the total number of time-steps. Our work sheds light on the bias-variance trade-off for tractable contextual bandits. This trade-off is not captured by algorithms that assume realizability, since under this assumption there exists an estimator in the class that attains zero bias.

Confidence Intervals for Policy Evaluation in Adaptive Experiments

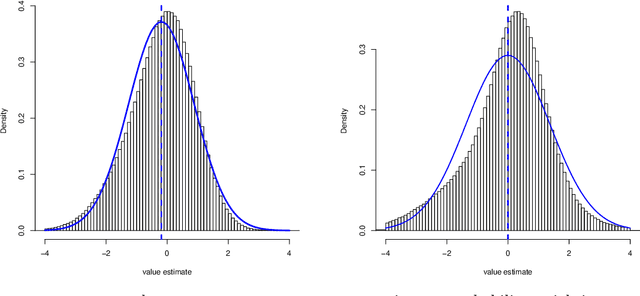
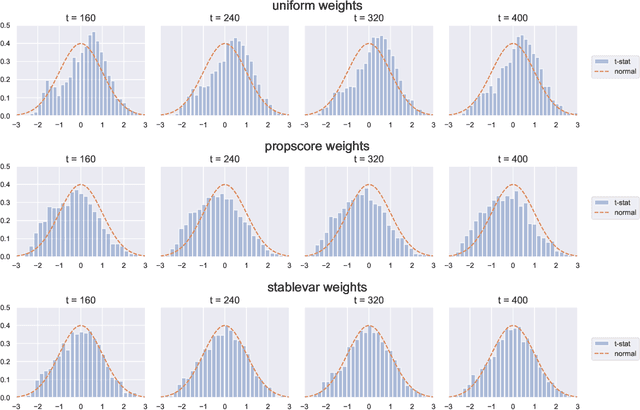
Adaptive experiments can result in considerable cost savings in multi-armed trials by enabling analysts to quickly focus on the most promising alternatives. Most existing work on adaptive experiments (which include multi-armed bandits) has focused maximizing the speed at which the analyst can identify the optimal arm and/or minimizing the number of draws from sub-optimal arms. In many scientific settings, however, it is not only of interest to identify the optimal arm, but also to perform a statistical analysis of the data collected from the experiment. Naive approaches to statistical inference with adaptive inference fail because many commonly used statistics (such as sample means or inverse propensity weighting) do not have an asymptotically Gaussian limiting distribution centered on the estimate, and so confidence intervals constructed from these statistics do not have correct coverage. But, as shown in this paper, carefully designed data-adaptive weighting schemes can be used to overcome this issue and restore a relevant central limit theorem, enabling hypothesis testing. We validate the accuracy of the resulting confidence intervals in numerical experiments.

Sufficient Representations for Categorical Variables

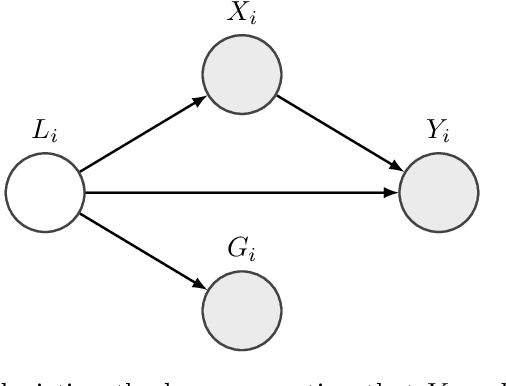
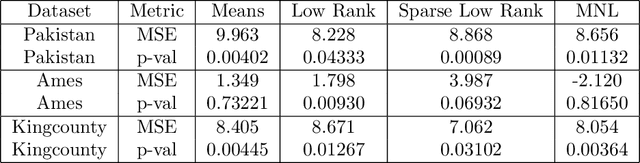
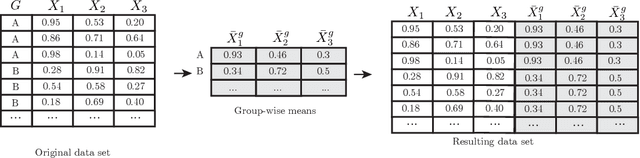
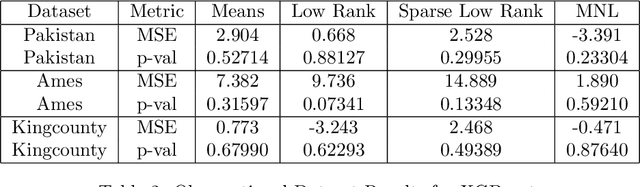
Many learning algorithms require categorical data to be transformed into real vectors before it can be used as input. Often, categorical variables are encoded as one-hot (or dummy) vectors. However, this mode of representation can be wasteful since it adds many low-signal regressors, especially when the number of unique categories is large. In this paper, we investigate simple alternative solutions for universally consistent estimators that rely on lower-dimensional real-valued representations of categorical variables that are "sufficient" in the sense that no predictive information is lost. We then compare preexisting and proposed methods on simulated and observational datasets.