Data-driven Error Estimation: Upper Bounding Multiple Errors with No Technical Debt

We formulate the problem of constructing multiple simultaneously valid confidence intervals (CIs) as estimating a high probability upper bound on the maximum error for a class/set of estimate-estimand-error tuples, and refer to this as the error estimation problem. For a single such tuple, data-driven confidence intervals can often be used to bound the error in our estimate. However, for a class of estimate-estimand-error tuples, nontrivial high probability upper bounds on the maximum error often require class complexity as input -- limiting the practicality of such methods and often resulting in loose bounds. Rather than deriving theoretical class complexity-based bounds, we propose a completely data-driven approach to estimate an upper bound on the maximum error. The simple and general nature of our solution to this fundamental challenge lends itself to several applications including: multiple CI construction, multiple hypothesis testing, estimating excess risk bounds (a fundamental measure of uncertainty in machine learning) for any training/fine-tuning algorithm, and enabling the development of a contextual bandit pipeline that can leverage any reward model estimation procedure as input (without additional mathematical analysis).

Proportional Response: Contextual Bandits for Simple and Cumulative Regret Minimization

Simple regret minimization is a critical problem in learning optimal treatment assignment policies across various domains, including healthcare and e-commerce. However, it remains understudied in the contextual bandit setting. We propose a new family of computationally efficient bandit algorithms for the stochastic contextual bandit settings, with the flexibility to be adapted for cumulative regret minimization (with near-optimal minimax guarantees) and simple regret minimization (with SOTA guarantees). Furthermore, our algorithms adapt to model misspecification and extend to the continuous arm settings. These advantages come from constructing and relying on "conformal arm sets" (CASs), which provide a set of arms at every context that encompass the context-specific optimal arm with some probability across the context distribution. Our positive results on simple and cumulative regret guarantees are contrasted by a negative result, which shows that an algorithm can't achieve instance-dependent simple regret guarantees while simultaneously achieving minimax optimal cumulative regret guarantees.

Selective Uncertainty Propagation in Offline RL

We study the finite-horizon offline reinforcement learning (RL) problem. Since actions at any state can affect next-state distributions, the related distributional shift challenges can make this problem far more statistically complex than offline policy learning for a finite sequence of stochastic contextual bandit environments. We formalize this insight by showing that the statistical hardness of offline RL instances can be measured by estimating the size of actions' impact on next-state distributions. Furthermore, this estimated impact allows us to propagate just enough value function uncertainty from future steps to avoid model exploitation, enabling us to develop algorithms that improve upon traditional pessimistic approaches for offline RL on statistically simple instances. Our approach is supported by theory and simulations.

Contextual Bandits in a Survey Experiment on Charitable Giving: Within-Experiment Outcomes versus Policy Learning

We design and implement an adaptive experiment (a ``contextual bandit'') to learn a targeted treatment assignment policy, where the goal is to use a participant's survey responses to determine which charity to expose them to in a donation solicitation. The design balances two competing objectives: optimizing the outcomes for the subjects in the experiment (``cumulative regret minimization'') and gathering data that will be most useful for policy learning, that is, for learning an assignment rule that will maximize welfare if used after the experiment (``simple regret minimization''). We evaluate alternative experimental designs by collecting pilot data and then conducting a simulation study. Next, we implement our selected algorithm. Finally, we perform a second simulation study anchored to the collected data that evaluates the benefits of the algorithm we chose. Our first result is that the value of a learned policy in this setting is higher when data is collected via a uniform randomization rather than collected adaptively using standard cumulative regret minimization or policy learning algorithms. We propose a simple heuristic for adaptive experimentation that improves upon uniform randomization from the perspective of policy learning at the expense of increasing cumulative regret relative to alternative bandit algorithms. The heuristic modifies an existing contextual bandit algorithm by (i) imposing a lower bound on assignment probabilities that decay slowly so that no arm is discarded too quickly, and (ii) after adaptively collecting data, restricting policy learning to select from arms where sufficient data has been gathered.

Flexible and Efficient Contextual Bandits with Heterogeneous Treatment Effect Oracle

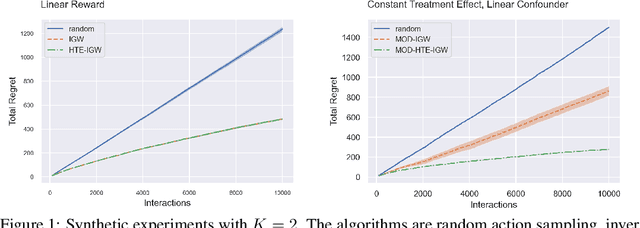
Many popular contextual bandit algorithms estimate reward models to inform decision making. However, true rewards can contain action-independent redundancies that are not relevant for decision making and only increase the statistical complexity of accurate estimation. It is sufficient and more data-efficient to estimate the simplest function that explains the reward differences between actions, that is, the heterogeneous treatment effect, commonly understood to be more structured and simpler than the reward. Motivated by this observation, building on recent work on oracle-based algorithms, we design a statistically optimal and computationally efficient algorithm using heterogeneous treatment effect estimation oracles. Our results provide the first universal reduction of contextual bandits to a general-purpose heterogeneous treatment effect estimation method. We show that our approach is more robust to model misspecification than reward estimation methods based on squared error regression oracles. Experimentally, we show the benefits of heterogeneous treatment effect estimation in contextual bandits over reward estimation.

Optimal Model Selection in Contextual Bandits with Many Classes via Offline Oracles

We study the problem of model selection for contextual bandits, in which the algorithm must balance the bias-variance trade-off for model estimation while also balancing the exploration-exploitation trade-off. In this paper, we propose the first reduction of model selection in contextual bandits to offline model selection oracles, allowing for flexible general purpose algorithms with computational requirements no worse than those for model selection for regression. Our main result is a new model selection guarantee for stochastic contextual bandits. When one of the classes in our set is realizable, up to a logarithmic dependency on the number of classes, our algorithm attains optimal realizability-based regret bounds for that class under one of two conditions: if the time-horizon is large enough, or if an assumption that helps with detecting misspecification holds. Hence our algorithm adapts to the complexity of this unknown class. Even when this realizable class is known, we prove improved regret guarantees in early rounds by relying on simpler model classes for those rounds and hence further establish the importance of model selection in contextual bandits.

Adapting to misspecification in contextual bandits with offline regression oracles

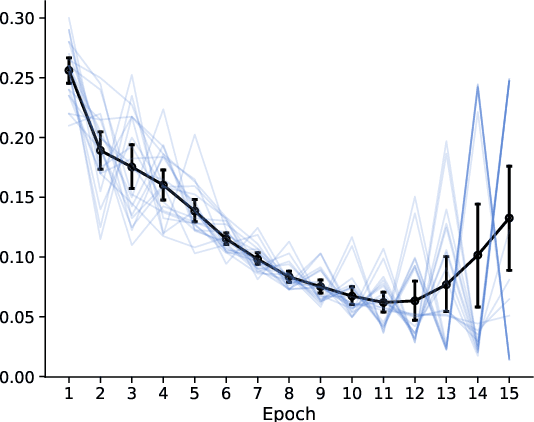
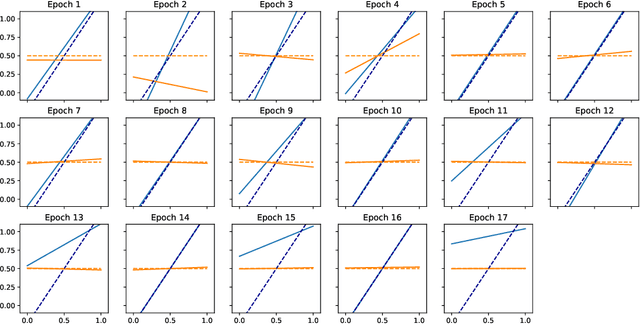
Computationally efficient contextual bandits are often based on estimating a predictive model of rewards given contexts and arms using past data. However, when the reward model is not well-specified, the bandit algorithm may incur unexpected regret, so recent work has focused on algorithms that are robust to misspecification. We propose a simple family of contextual bandit algorithms that adapt to misspecification error by reverting to a good safe policy when there is evidence that misspecification is causing a regret increase. Our algorithm requires only an offline regression oracle to ensure regret guarantees that gracefully degrade in terms of a measure of the average misspecification level. Compared to prior work, we attain similar regret guarantees, but we do no rely on a master algorithm, and do not require more robust oracles like online or constrained regression oracles (e.g., Foster et al. (2020a); Krishnamurthy et al. (2020)). This allows us to design algorithms for more general function approximation classes.

Tractable contextual bandits beyond realizability

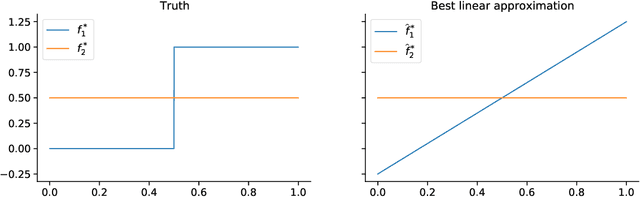
Tractable contextual bandit algorithms often rely on the realizability assumption -- i.e., that the true expected reward model belongs to a known class, such as linear functions. We investigate issues that arise in the absence of realizability and note that the dynamics of adaptive data collection can lead commonly used bandit algorithms to learn a suboptimal policy. In this work, we present a tractable bandit algorithm that is not sensitive to the realizability assumption and computationally reduces to solving a constrained regression problem in every epoch. When realizability does not hold, our algorithm ensures the same guarantees on regret achieved by realizability-based algorithms under realizability, up to an additive term that accounts for the misspecification error. This extra term is proportional to T times the (2/5)-root of the mean squared error between the best model in the class and the true model, where T is the total number of time-steps. Our work sheds light on the bias-variance trade-off for tractable contextual bandits. This trade-off is not captured by algorithms that assume realizability, since under this assumption there exists an estimator in the class that attains zero bias.

Survey Bandits with Regret Guarantees

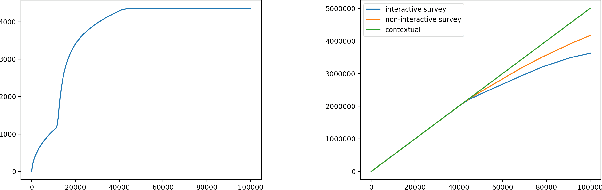
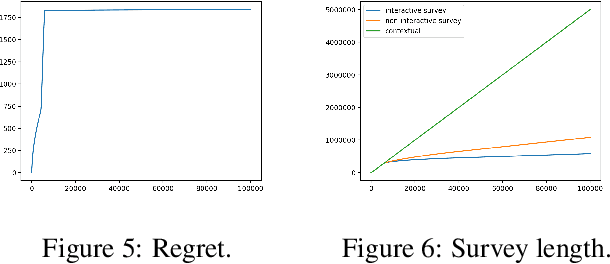
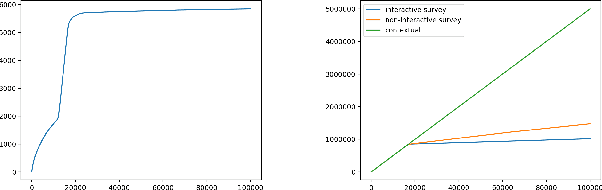
We consider a variant of the contextual bandit problem. In standard contextual bandits, when a user arrives we get the user's complete feature vector and then assign a treatment (arm) to that user. In a number of applications (like healthcare), collecting features from users can be costly. To address this issue, we propose algorithms that avoid needless feature collection while maintaining strong regret guarantees.

Groupwise Maximin Fair Allocation of Indivisible Goods

We study the problem of allocating indivisible goods among n agents in a fair manner. For this problem, maximin share (MMS) is a well-studied solution concept which provides a fairness threshold. Specifically, maximin share is defined as the minimum utility that an agent can guarantee for herself when asked to partition the set of goods into n bundles such that the remaining (n-1) agents pick their bundles adversarially. An allocation is deemed to be fair if every agent gets a bundle whose valuation is at least her maximin share. Even though maximin shares provide a natural benchmark for fairness, it has its own drawbacks and, in particular, it is not sufficient to rule out unsatisfactory allocations. Motivated by these considerations, in this work we define a stronger notion of fairness, called groupwise maximin share guarantee (GMMS). In GMMS, we require that the maximin share guarantee is achieved not just with respect to the grand bundle, but also among all the subgroups of agents. Hence, this solution concept strengthens MMS and provides an ex-post fairness guarantee. We show that in specific settings, GMMS allocations always exist. We also establish the existence of approximate GMMS allocations under additive valuations, and develop a polynomial-time algorithm to find such allocations. Moreover, we establish a scale of fairness wherein we show that GMMS implies approximate envy freeness. Finally, we empirically demonstrate the existence of GMMS allocations in a large set of randomly generated instances. For the same set of instances, we additionally show that our algorithm achieves an approximation factor better than the established, worst-case bound.