Tractable contextual bandits beyond realizability

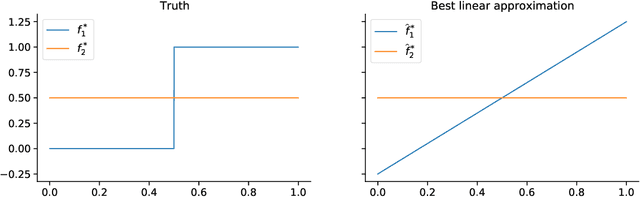
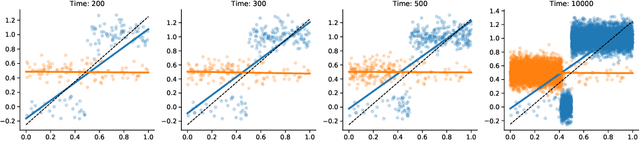
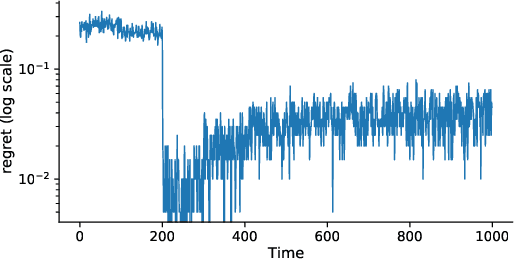
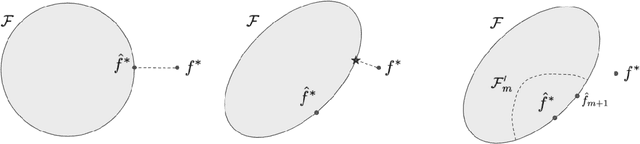
Tractable contextual bandit algorithms often rely on the realizability assumption -- i.e., that the true expected reward model belongs to a known class, such as linear functions. We investigate issues that arise in the absence of realizability and note that the dynamics of adaptive data collection can lead commonly used bandit algorithms to learn a suboptimal policy. In this work, we present a tractable bandit algorithm that is not sensitive to the realizability assumption and computationally reduces to solving a constrained regression problem in every epoch. When realizability does not hold, our algorithm ensures the same guarantees on regret achieved by realizability-based algorithms under realizability, up to an additive term that accounts for the misspecification error. This extra term is proportional to T times the (2/5)-root of the mean squared error between the best model in the class and the true model, where T is the total number of time-steps. Our work sheds light on the bias-variance trade-off for tractable contextual bandits. This trade-off is not captured by algorithms that assume realizability, since under this assumption there exists an estimator in the class that attains zero bias.