Y. Narahari
Indian Institute of Science
Deep Learning Meets Mechanism Design: Key Results and Some Novel Applications
Jan 11, 2024Abstract:Mechanism design is essentially reverse engineering of games and involves inducing a game among strategic agents in a way that the induced game satisfies a set of desired properties in an equilibrium of the game. Desirable properties for a mechanism include incentive compatibility, individual rationality, welfare maximisation, revenue maximisation (or cost minimisation), fairness of allocation, etc. It is known from mechanism design theory that only certain strict subsets of these properties can be simultaneously satisfied exactly by any given mechanism. Often, the mechanisms required by real-world applications may need a subset of these properties that are theoretically impossible to be simultaneously satisfied. In such cases, a prominent recent approach is to use a deep learning based approach to learn a mechanism that approximately satisfies the required properties by minimizing a suitably defined loss function. In this paper, we present, from relevant literature, technical details of using a deep learning approach for mechanism design and provide an overview of key results in this topic. We demonstrate the power of this approach for three illustrative case studies: (a) efficient energy management in a vehicular network (b) resource allocation in a mobile network (c) designing a volume discount procurement auction for agricultural inputs. Section 6 concludes the paper.
An innovative Deep Learning Based Approach for Accurate Agricultural Crop Price Prediction
Apr 15, 2023Abstract:Accurate prediction of agricultural crop prices is a crucial input for decision-making by various stakeholders in agriculture: farmers, consumers, retailers, wholesalers, and the Government. These decisions have significant implications including, most importantly, the economic well-being of the farmers. In this paper, our objective is to accurately predict crop prices using historical price information, climate conditions, soil type, location, and other key determinants of crop prices. This is a technically challenging problem, which has been attempted before. In this paper, we propose an innovative deep learning based approach to achieve increased accuracy in price prediction. The proposed approach uses graph neural networks (GNNs) in conjunction with a standard convolutional neural network (CNN) model to exploit geospatial dependencies in prices. Our approach works well with noisy legacy data and produces a performance that is at least 20% better than the results available in the literature. We are able to predict prices up to 30 days ahead. We choose two vegetables, potato (stable price behavior) and tomato (volatile price behavior) and work with noisy public data available from Indian agricultural markets.
Maxmin Participatory Budgeting
Apr 29, 2022
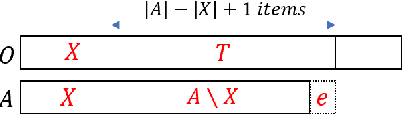
Abstract:Participatory Budgeting (PB) is a popular voting method by which a limited budget is divided among a set of projects, based on the preferences of voters over the projects. PB is broadly categorised as divisible PB (if the projects are fractionally implementable) and indivisible PB (if the projects are atomic). Egalitarianism, an important objective in PB, has not received much attention in the context of indivisible PB. This paper addresses this gap through a detailed study of a natural egalitarian rule, Maxmin Participatory Budgeting (MPB), in the context of indivisible PB. Our study is in two parts: (1) computational (2) axiomatic. In the first part, we prove that MPB is computationally hard and give pseudo-polynomial time and polynomial-time algorithms when parameterized by certain well-motivated parameters. We propose an algorithm that achieves for MPB, additive approximation guarantees for restricted spaces of instances and empirically show that our algorithm in fact gives exact optimal solutions on real-world PB datasets. We also establish an upper bound on the approximation ratio achievable for MPB by the family of exhaustive strategy-proof PB algorithms. In the second part, we undertake an axiomatic study of the MPB rule by generalizing known axioms in the literature. Our study leads to the proposal of a new axiom, maximal coverage, which captures fairness aspects. We prove that MPB satisfies maximal coverage.
Ballooning Multi-Armed Bandits
Jan 24, 2020
Abstract:In this paper, we introduce Ballooning Multi-Armed Bandits (BL-MAB), a novel extension to the classical stochastic MAB model. In BL-MAB model, the set of available arms grows (or balloons) over time. In contrast to the classical MAB setting where the regret is computed with respect to the best arm overall, the regret in a BL-MAB setting is computed with respect to the best available arm at each time. We first observe that the existing MAB algorithms are not regret-optimal for the BL-MAB model. We show that if the best arm is equally likely to arrive at any time, a sub-linear regret cannot be achieved, irrespective of the arrival of other arms. We further show that if the best arm is more likely to arrive in the early rounds, one can achieve sub-linear regret. Our proposed algorithm determines (1) the fraction of the time horizon for which the newly arriving arms should be explored and (2) the sequence of arm pulls in the exploitation phase from among the explored arms. Making reasonable assumptions on the arrival distribution of the best arm in terms of the thinness of the distribution's tail, we prove that the proposed algorithm achieves sub-linear instance-independent regret. We further quantify the explicit dependence of regret on the arrival distribution parameters. We reinforce our theoretical findings with extensive simulation results.
Achieving Fairness in the Stochastic Multi-armed Bandit Problem
Jul 23, 2019
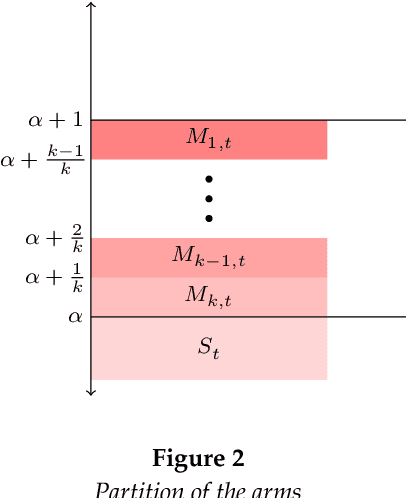
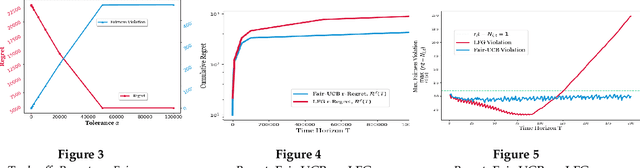
Abstract:We study an interesting variant of the stochastic multi-armed bandit problem, called the Fair-SMAB problem, where each arm is required to be pulled for at least a given fraction of the total available rounds. We investigate the interplay between learning and fairness in terms of a pre-specified vector denoting the fractions of guaranteed pulls. We define a fairness-aware regret, called $r$-Regret, that takes into account the above fairness constraints and naturally extends the conventional notion of regret. Our primary contribution is characterizing a class of Fair-SMAB algorithms by two parameters: the unfairness tolerance and the learning algorithm used as a black-box. We provide a fairness guarantee for this class that holds uniformly over time irrespective of the choice of the learning algorithm. In particular, when the learning algorithm is UCB1, we show that our algorithm achieves $O(\ln T)$ $r$-Regret. Finally, we evaluate the cost of fairness in terms of the conventional notion of regret.
Stochastic Multi-armed Bandits with Arm-specific Fairness Guarantees
May 27, 2019


Abstract:We study an interesting variant of the stochastic multi-armed bandit problem in which each arm is required to be pulled for at least a given fraction of the total available rounds. We investigate the interplay between learning and fairness in terms of a pre-specified vector specifying the fractions of guaranteed pulls. We define a Fairness-aware regret that takes into account the above fairness constraints and extends the conventional notion of regret in a natural way. We show that logarithmic regret can be achieved while (almost) satisfying the fairness requirements. In contrast to the current literature where the fairness notion is instance dependent, we consider that the fairness criterion is exogenously specified as an input to the algorithm. Our regret guarantee is universal i.e. holds for any given fairness vector.
Groupwise Maximin Fair Allocation of Indivisible Goods
Nov 21, 2017Abstract:We study the problem of allocating indivisible goods among n agents in a fair manner. For this problem, maximin share (MMS) is a well-studied solution concept which provides a fairness threshold. Specifically, maximin share is defined as the minimum utility that an agent can guarantee for herself when asked to partition the set of goods into n bundles such that the remaining (n-1) agents pick their bundles adversarially. An allocation is deemed to be fair if every agent gets a bundle whose valuation is at least her maximin share. Even though maximin shares provide a natural benchmark for fairness, it has its own drawbacks and, in particular, it is not sufficient to rule out unsatisfactory allocations. Motivated by these considerations, in this work we define a stronger notion of fairness, called groupwise maximin share guarantee (GMMS). In GMMS, we require that the maximin share guarantee is achieved not just with respect to the grand bundle, but also among all the subgroups of agents. Hence, this solution concept strengthens MMS and provides an ex-post fairness guarantee. We show that in specific settings, GMMS allocations always exist. We also establish the existence of approximate GMMS allocations under additive valuations, and develop a polynomial-time algorithm to find such allocations. Moreover, we establish a scale of fairness wherein we show that GMMS implies approximate envy freeness. Finally, we empirically demonstrate the existence of GMMS allocations in a large set of randomly generated instances. For the same set of instances, we additionally show that our algorithm achieves an approximation factor better than the established, worst-case bound.
Complexity of Manipulation with Partial Information in Voting
Jul 13, 2017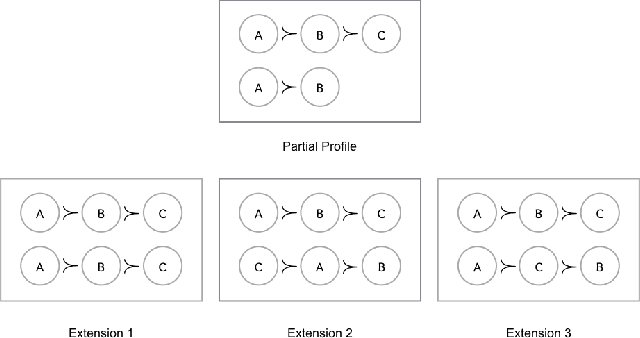
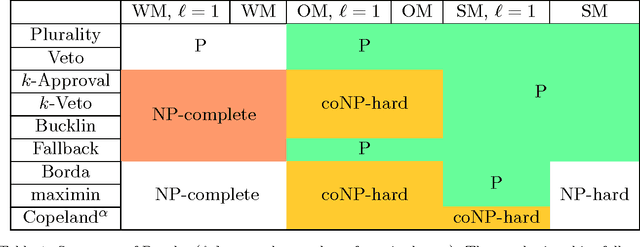

Abstract:The Coalitional Manipulation problem has been studied extensively in the literature for many voting rules. However, most studies have focused on the complete information setting, wherein the manipulators know the votes of the non-manipulators. While this assumption is reasonable for purposes of showing intractability, it is unrealistic for algorithmic considerations. In most real-world scenarios, it is impractical for the manipulators to have accurate knowledge of all the other votes. In this paper, we investigate manipulation with incomplete information. In our framework, the manipulators know a partial order for each voter that is consistent with the true preference of that voter. In this setting, we formulate three natural computational notions of manipulation, namely weak, opportunistic, and strong manipulation. We say that an extension of a partial order is if there exists a manipulative vote for that extension. 1. Weak Manipulation (WM): the manipulators seek to vote in a way that makes their preferred candidate win in at least one extension of the partial votes of the non-manipulators. 2. Opportunistic Manipulation (OM): the manipulators seek to vote in a way that makes their preferred candidate win in every viable extension of the partial votes of the non-manipulators. 3. Strong Manipulation (SM): the manipulators seek to vote in a way that makes their preferred candidate win in every extension of the partial votes of the non-manipulators. We consider several scenarios for which the traditional manipulation problems are easy (for instance, Borda with a single manipulator). For many of them, the corresponding manipulative questions that we propose turn out to be computationally intractable. Our hardness results often hold even when very little information is missing, or in other words, even when the instances are quite close to the complete information setting.
Frugal Bribery in Voting
Feb 28, 2017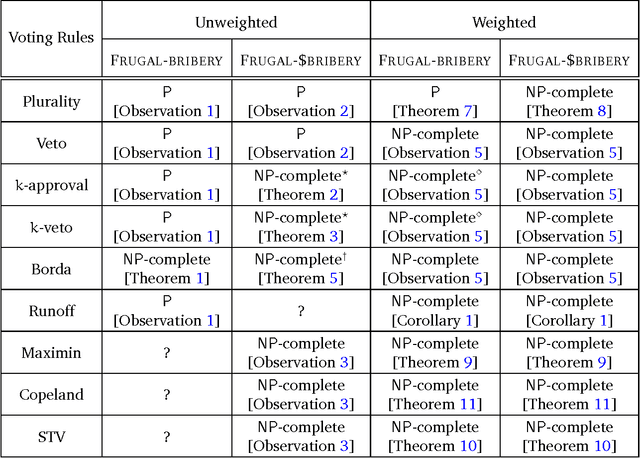

Abstract:Bribery in elections is an important problem in computational social choice theory. However, bribery with money is often illegal in elections. Motivated by this, we introduce the notion of frugal bribery and formulate two new pertinent computational problems which we call Frugal-bribery and Frugal- $bribery to capture bribery without money in elections. In the proposed model, the briber is frugal in nature and this is captured by her inability to bribe votes of a certain kind, namely, non-vulnerable votes. In the Frugal-bribery problem, the goal is to make a certain candidate win the election by changing only vulnerable votes. In the Frugal-{dollar}bribery problem, the vulnerable votes have prices and the goal is to make a certain candidate win the election by changing only vulnerable votes, subject to a budget constraint of the briber. We further formulate two natural variants of the Frugal-{dollar}bribery problem namely Uniform-frugal-{dollar}bribery and Nonuniform-frugal-{dollar}bribery where the prices of the vulnerable votes are, respectively, all the same or different. We study the computational complexity of the above problems for unweighted and weighted elections for several commonly used voting rules. We observe that, even if we have only a small number of candidates, the problems are intractable for all voting rules studied here for weighted elections, with the sole exception of the Frugal-bribery problem for the plurality voting rule. In contrast, we have polynomial time algorithms for the Frugal-bribery problem for plurality, veto, k-approval, k-veto, and plurality with runoff voting rules for unweighted elections. However, the Frugal-{dollar}bribery problem is intractable for all the voting rules studied here barring the plurality and the veto voting rules for unweighted elections.
An Iterative Transfer Learning Based Ensemble Technique for Automatic Short Answer Grading
Nov 21, 2016



Abstract:Automatic short answer grading (ASAG) techniques are designed to automatically assess short answers to questions in natural language, having a length of a few words to a few sentences. Supervised ASAG techniques have been demonstrated to be effective but suffer from a couple of key practical limitations. They are greatly reliant on instructor provided model answers and need labeled training data in the form of graded student answers for every assessment task. To overcome these, in this paper, we introduce an ASAG technique with two novel features. We propose an iterative technique on an ensemble of (a) a text classifier of student answers and (b) a classifier using numeric features derived from various similarity measures with respect to model answers. Second, we employ canonical correlation analysis based transfer learning on a common feature representation to build the classifier ensemble for questions having no labelled data. The proposed technique handsomely beats all winning supervised entries on the SCIENTSBANK dataset from the Student Response Analysis task of SemEval 2013. Additionally, we demonstrate generalizability and benefits of the proposed technique through evaluation on multiple ASAG datasets from different subject topics and standards.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge