Neeldhara Misra
Parameterized Aspects of Distinct Kemeny Rank Aggregation
Sep 07, 2023Abstract:The Kemeny method is one of the popular tools for rank aggregation. However, computing an optimal Kemeny ranking is NP-hard. Consequently, the computational task of finding a Kemeny ranking has been studied under the lens of parameterized complexity with respect to many parameters. We first present a comprehensive relationship, both theoretical and empirical, among these parameters. Further, we study the problem of computing all distinct Kemeny rankings under the lens of parameterized complexity. We consider the target Kemeny score, number of candidates, average distance of input rankings, maximum range of any candidate, and unanimity width as our parameters. For all these parameters, we already have FPT algorithms. We find that any desirable number of Kemeny rankings can also be found without substantial increase in running time. We also present FPT approximation algorithms for Kemeny rank aggregation with respect to these parameters.
A Parameterized Perspective on Protecting Elections
May 28, 2019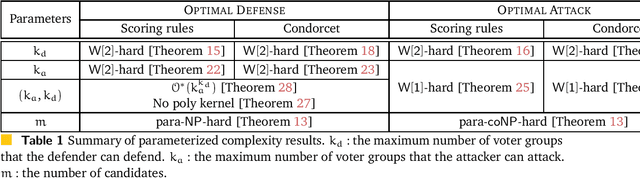

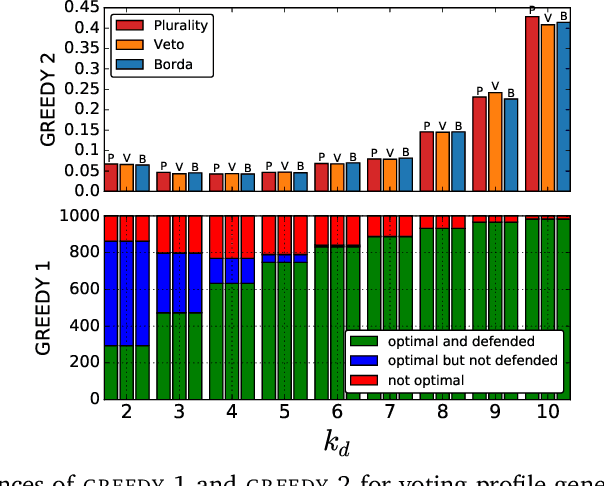
Abstract:We study the parameterized complexity of the optimal defense and optimal attack problems in voting. In both the problems, the input is a set of voter groups (every voter group is a set of votes) and two integers $k_a$ and $k_d$ corresponding to respectively the number of voter groups the attacker can attack and the number of voter groups the defender can defend. A voter group gets removed from the election if it is attacked but not defended. In the optimal defense problem, we want to know if it is possible for the defender to commit to a strategy of defending at most $k_d$ voter groups such that, no matter which $k_a$ voter groups the attacker attacks, the outcome of the election does not change. In the optimal attack problem, we want to know if it is possible for the attacker to commit to a strategy of attacking $k_a$ voter groups such that, no matter which $k_d$ voter groups the defender defends, the outcome of the election is always different from the original (without any attack) one.
Complexity of Manipulation with Partial Information in Voting
Jul 13, 2017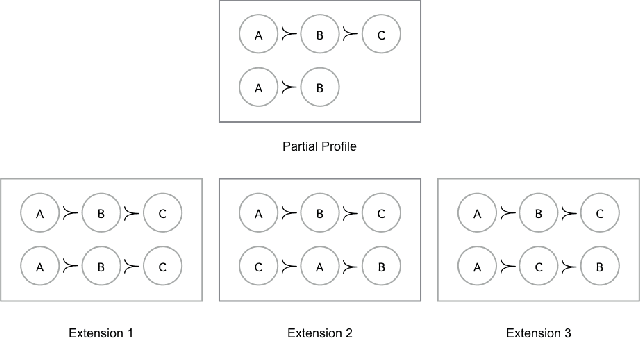
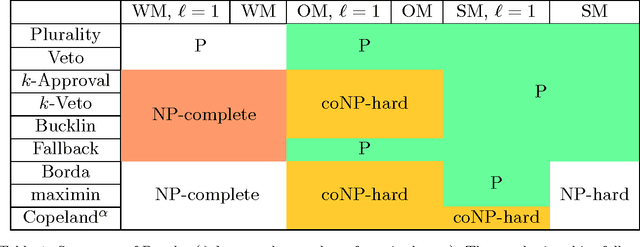

Abstract:The Coalitional Manipulation problem has been studied extensively in the literature for many voting rules. However, most studies have focused on the complete information setting, wherein the manipulators know the votes of the non-manipulators. While this assumption is reasonable for purposes of showing intractability, it is unrealistic for algorithmic considerations. In most real-world scenarios, it is impractical for the manipulators to have accurate knowledge of all the other votes. In this paper, we investigate manipulation with incomplete information. In our framework, the manipulators know a partial order for each voter that is consistent with the true preference of that voter. In this setting, we formulate three natural computational notions of manipulation, namely weak, opportunistic, and strong manipulation. We say that an extension of a partial order is if there exists a manipulative vote for that extension. 1. Weak Manipulation (WM): the manipulators seek to vote in a way that makes their preferred candidate win in at least one extension of the partial votes of the non-manipulators. 2. Opportunistic Manipulation (OM): the manipulators seek to vote in a way that makes their preferred candidate win in every viable extension of the partial votes of the non-manipulators. 3. Strong Manipulation (SM): the manipulators seek to vote in a way that makes their preferred candidate win in every extension of the partial votes of the non-manipulators. We consider several scenarios for which the traditional manipulation problems are easy (for instance, Borda with a single manipulator). For many of them, the corresponding manipulative questions that we propose turn out to be computationally intractable. Our hardness results often hold even when very little information is missing, or in other words, even when the instances are quite close to the complete information setting.
Frugal Bribery in Voting
Feb 28, 2017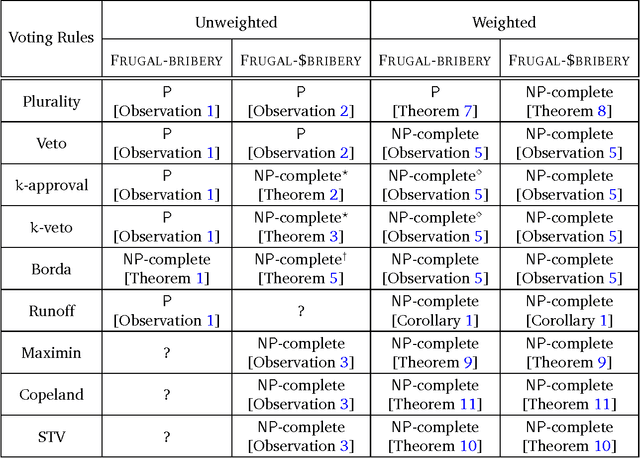

Abstract:Bribery in elections is an important problem in computational social choice theory. However, bribery with money is often illegal in elections. Motivated by this, we introduce the notion of frugal bribery and formulate two new pertinent computational problems which we call Frugal-bribery and Frugal- $bribery to capture bribery without money in elections. In the proposed model, the briber is frugal in nature and this is captured by her inability to bribe votes of a certain kind, namely, non-vulnerable votes. In the Frugal-bribery problem, the goal is to make a certain candidate win the election by changing only vulnerable votes. In the Frugal-{dollar}bribery problem, the vulnerable votes have prices and the goal is to make a certain candidate win the election by changing only vulnerable votes, subject to a budget constraint of the briber. We further formulate two natural variants of the Frugal-{dollar}bribery problem namely Uniform-frugal-{dollar}bribery and Nonuniform-frugal-{dollar}bribery where the prices of the vulnerable votes are, respectively, all the same or different. We study the computational complexity of the above problems for unweighted and weighted elections for several commonly used voting rules. We observe that, even if we have only a small number of candidates, the problems are intractable for all voting rules studied here for weighted elections, with the sole exception of the Frugal-bribery problem for the plurality voting rule. In contrast, we have polynomial time algorithms for the Frugal-bribery problem for plurality, veto, k-approval, k-veto, and plurality with runoff voting rules for unweighted elections. However, the Frugal-{dollar}bribery problem is intractable for all the voting rules studied here barring the plurality and the veto voting rules for unweighted elections.
Backdoors into Heterogeneous Classes of SAT and CSP
Oct 25, 2016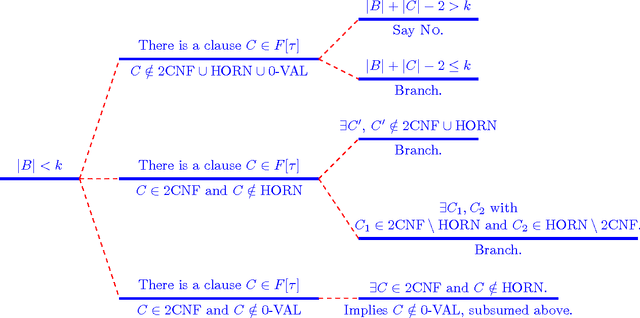
Abstract:In this paper we extend the classical notion of strong and weak backdoor sets for SAT and CSP by allowing that different instantiations of the backdoor variables result in instances that belong to different base classes; the union of the base classes forms a heterogeneous base class. Backdoor sets to heterogeneous base classes can be much smaller than backdoor sets to homogeneous ones, hence they are much more desirable but possibly harder to find. We draw a detailed complexity landscape for the problem of detecting strong and weak backdoor sets into heterogeneous base classes for SAT and CSP.
* to appear in JCSS, full version of an AAAI 2014 paper
Preference Elicitation For Single Crossing Domain
Apr 15, 2016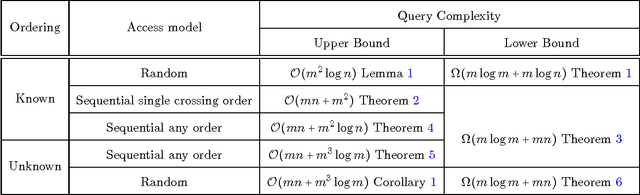
Abstract:Eliciting the preferences of a set of agents over a set of alternatives is a problem of fundamental importance in social choice theory. Prior work on this problem has studied the query complexity of preference elicitation for the unrestricted domain and for the domain of single peaked preferences. In this paper, we consider the domain of single crossing preference profiles and study the query complexity of preference elicitation under various settings. We consider two distinct situations: when an ordering of the voters with respect to which the profile is single crossing is known versus when it is unknown. We also consider different access models: when the votes can be accessed at random, as opposed to when they are coming in a pre-defined sequence. In the sequential access model, we distinguish two cases when the ordering is known: the first is that sequence in which the votes appear is also a single-crossing order, versus when it is not. The main contribution of our work is to provide polynomial time algorithms with low query complexity for preference elicitation in all the above six cases. Further, we show that the query complexities of our algorithms are optimal up to constant factors for all but one of the above six cases. We then present preference elicitation algorithms for profiles which are close to being single crossing under various notions of closeness, for example, single crossing width, minimum number of candidates | voters whose deletion makes a profile single crossing.
Elicitation for Preferences Single Peaked on Trees
Apr 15, 2016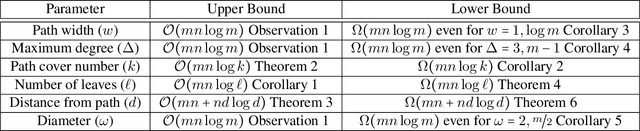
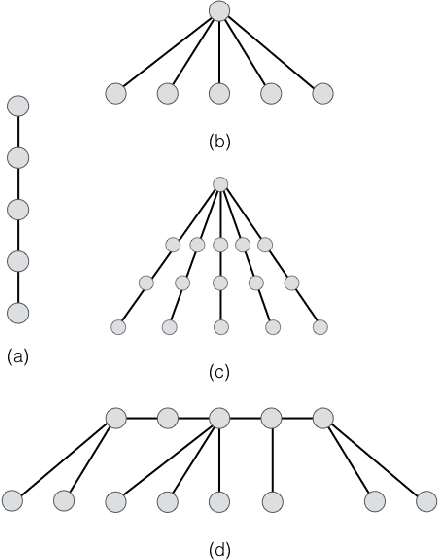
Abstract:In multiagent systems, we often have a set of agents each of which have a preference ordering over a set of items and one would like to know these preference orderings for various tasks, for example, data analysis, preference aggregation, voting etc. However, we often have a large number of items which makes it impractical to ask the agents for their complete preference ordering. In such scenarios, we usually elicit these agents' preferences by asking (a hopefully small number of) comparison queries --- asking an agent to compare two items. Prior works on preference elicitation focus on unrestricted domain and the domain of single peaked preferences and show that the preferences in single peaked domain can be elicited by much less number of queries compared to unrestricted domain. We extend this line of research and study preference elicitation for single peaked preferences on trees which is a strict superset of the domain of single peaked preferences. We show that the query complexity crucially depends on the number of leaves, the path cover number, and the distance from path of the underlying single peaked tree, whereas the other natural parameters like maximum degree, diameter, pathwidth do not play any direct role in determining query complexity. We then investigate the query complexity for finding a weak Condorcet winner for preferences single peaked on a tree and show that this task has much less query complexity than preference elicitation. Here again we observe that the number of leaves in the underlying single peaked tree and the path cover number of the tree influence the query complexity of the problem.
On Choosing Committees Based on Approval Votes in the Presence of Outliers
Nov 13, 2015
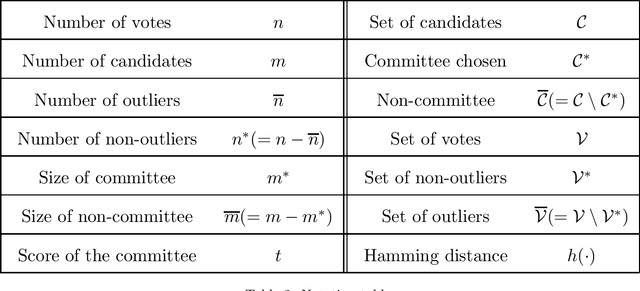
Abstract:We study the computational complexity of committee selection problem for several approval-based voting rules in the presence of outliers. Our first result shows that outlier consideration makes committee selection problem intractable for approval, net approval, and minisum approval voting rules. We then study parameterized complexity of this problem with five natural parameters, namely the target score, the size of the committee (and its dual parameter, the number of candidates outside the committee), the number of outliers (and its dual parameter, the number of non-outliers). For net approval and minisum approval voting rules, we provide a dichotomous result, resolving the parameterized complexity of this problem for all subsets of five natural parameters considered (by showing either FPT or W[1]-hardness for all subsets of parameters). For the approval voting rule, we resolve the parameterized complexity of this problem for all subsets of parameters except one. We also study approximation algorithms for this problem. We show that there does not exist any alpha(.) factor approximation algorithm for approval and net approval voting rules, for any computable function alpha(.), unless P=NP. For the minisum voting rule, we provide a pseudopolynomial (1+eps) factor approximation algorithm.
Manipulation is Harder with Incomplete Votes
Apr 30, 2015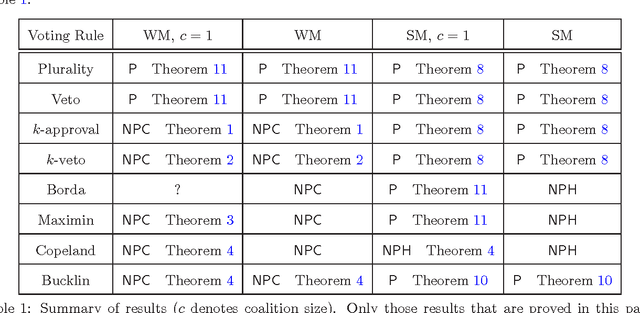
Abstract:The Coalitional Manipulation (CM) problem has been studied extensively in the literature for many voting rules. The CM problem, however, has been studied only in the complete information setting, that is, when the manipulators know the votes of the non-manipulators. A more realistic scenario is an incomplete information setting where the manipulators do not know the exact votes of the non- manipulators but may have some partial knowledge of the votes. In this paper, we study a setting where the manipulators know a partial order for each voter that is consistent with the vote of that voter. In this setting, we introduce and study two natural computational problems - (1) Weak Manipulation (WM) problem where the manipulators wish to vote in a way that makes their preferred candidate win in at least one extension of the partial votes of the non-manipulators; (2) Strong Manipulation (SM) problem where the manipulators wish to vote in a way that makes their preferred candidate win in all possible extensions of the partial votes of the non-manipulators. We study the computational complexity of the WM and the SM problems for commonly used voting rules such as plurality, veto, k-approval, k-veto, maximin, Copeland, and Bucklin. Our key finding is that, barring a few exceptions, manipulation becomes a significantly harder problem in the setting of incomplete votes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge