Projection-free Algorithms for Online Convex Optimization with Adversarial Constraints

We study a generalization of the Online Convex Optimization (OCO) framework with time-varying adversarial constraints. In this problem, after selecting a feasible action from the convex decision set $X,$ a convex constraint function is revealed alongside the cost function in each round. Our goal is to design a computationally efficient learning policy that achieves a small regret with respect to the cost functions and a small cumulative constraint violation (CCV) with respect to the constraint functions over a horizon of length $T$. It is well-known that the projection step constitutes the major computational bottleneck of the standard OCO algorithms. However, for many structured decision sets, linear functions can be efficiently optimized over the decision set. We propose a *projection-free* online policy which makes a single call to a Linear Program (LP) solver per round. Our method outperforms state-of-the-art projection-free online algorithms with adversarial constraints, achieving improved bounds of $\tilde{O}(T^{\frac{3}{4}})$ for both regret and CCV. The proposed algorithm is conceptually simple - it first constructs a surrogate cost function as a non-negative linear combination of the cost and constraint functions. Then, it passes the surrogate costs to a new, adaptive version of the online conditional gradient subroutine, which we propose in this paper.

Parameterized Aspects of Distinct Kemeny Rank Aggregation

The Kemeny method is one of the popular tools for rank aggregation. However, computing an optimal Kemeny ranking is NP-hard. Consequently, the computational task of finding a Kemeny ranking has been studied under the lens of parameterized complexity with respect to many parameters. We first present a comprehensive relationship, both theoretical and empirical, among these parameters. Further, we study the problem of computing all distinct Kemeny rankings under the lens of parameterized complexity. We consider the target Kemeny score, number of candidates, average distance of input rankings, maximum range of any candidate, and unanimity width as our parameters. For all these parameters, we already have FPT algorithms. We find that any desirable number of Kemeny rankings can also be found without substantial increase in running time. We also present FPT approximation algorithms for Kemeny rank aggregation with respect to these parameters.

Knapsack: Connectedness, Path, and Shortest-Path

We study the knapsack problem with graph theoretic constraints. That is, we assume that there exists a graph structure on the set of items of knapsack and the solution also needs to satisfy certain graph theoretic properties on top of knapsack constraints. In particular, we need to compute in the connected knapsack problem a connected subset of items which has maximum value subject to the size of knapsack constraint. We show that this problem is strongly NP-complete even for graphs of maximum degree four and NP-complete even for star graphs. On the other hand, we develop an algorithm running in time $O\left(2^{tw\log tw}\cdot\text{poly}(\min\{s^2,d^2\})\right)$ where $tw,s,d$ are respectively treewidth of the graph, size, and target value of the knapsack. We further exhibit a $(1-\epsilon)$ factor approximation algorithm running in time $O\left(2^{tw\log tw}\cdot\text{poly}(n,1/\epsilon)\right)$ for every $\epsilon>0$. We show similar results for several other graph theoretic properties, namely path and shortest-path under the problem names path-knapsack and shortestpath-knapsack. Our results seems to indicate that connected-knapsack is computationally hardest followed by path-knapsack and shortestpath-knapsack.

Sampling-Based Winner Prediction in District-Based Elections

In a district-based election, we apply a voting rule $r$ to decide the winners in each district, and a candidate who wins in a maximum number of districts is the winner of the election. We present efficient sampling-based algorithms to predict the winner of such district-based election systems in this paper. When $r$ is plurality and the margin of victory is known to be at least $\varepsilon$ fraction of the total population, we present an algorithm to predict the winner. The sample complexity of our algorithm is $\mathcal{O}\left(\frac{1}{\varepsilon^4}\log \frac{1}{\varepsilon}\log\frac{1}{\delta}\right)$. We complement this result by proving that any algorithm, from a natural class of algorithms, for predicting the winner in a district-based election when $r$ is plurality, must sample at least $\Omega\left(\frac{1}{\varepsilon^4}\log\frac{1}{\delta}\right)$ votes. We then extend this result to any voting rule $r$. Loosely speaking, we show that we can predict the winner of a district-based election with an extra overhead of $\mathcal{O}\left(\frac{1}{\varepsilon^2}\log\frac{1}{\delta}\right)$ over the sample complexity of predicting the single-district winner under $r$. We further extend our algorithm for the case when the margin of victory is unknown, but we have only two candidates. We then consider the median voting rule when the set of preferences in each district is single-peaked. We show that the winner of a district-based election can be predicted with $\mathcal{O}\left(\frac{1}{\varepsilon^4}\log\frac{1}{\varepsilon}\log\frac{1}{\delta}\right)$ samples even when the harmonious order in different districts can be different and even unknown. Finally, we also show some results for estimating the margin of victory of a district-based election within both additive and multiplicative error bounds.

Feature-based Individual Fairness in k-Clustering

Ensuring fairness in machine learning algorithms is a challenging and important task. We consider the problem of clustering a set of points while ensuring fairness constraints. While there have been several attempts to capture group fairness in the k-clustering problem, fairness at an individual level is not well-studied. We introduce a new notion of individual fairness in k-clustering based on features that are not necessarily used for clustering. We show that this problem is NP-hard and does not admit a constant factor approximation. We then design a randomized algorithm that guarantees approximation both in terms of minimizing the clustering distance objective as well as individual fairness under natural restrictions on the distance metric and fairness constraints. Finally, our experimental results validate that our algorithm produces lower clustering costs compared to existing algorithms while being competitive in individual fairness.

Stable Manipulation in Voting

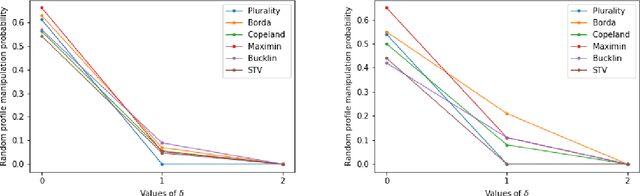
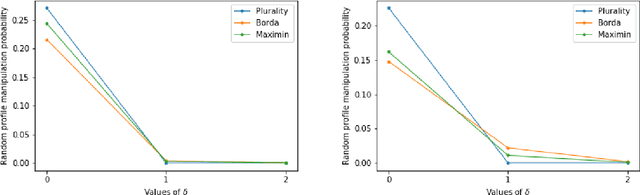
We introduce the problem of {\em stable manipulation} where the manipulators need to compute if there exist votes for the manipulators which make their preferred alternative win the election even if the manipulators' knowledge about others' votes are little inaccurate, that is, manipulation remains successful even under small perturbation of the non-manipulators' votes. We show that every scoring rule, maximin, Bucklin, and simplified Bucklin voting rules are stably manipulable in polynomial time for single manipulator. In contrast, stable manipulation becomes intractable for the Copeland$^\alpha$ voting rule for every $\alpha\in[0,1]$ even for single manipulator. However for a constant number of alternatives, we show that the stable manipulation problem is polynomial time solvable for every anonymous and efficient voting rules. Finally we empirically show that the probability that a uniformly random profile is stably manipulable decreases drastically even if manipulator possess little uncertainty about others' votes.

A Parameterized Perspective on Protecting Elections

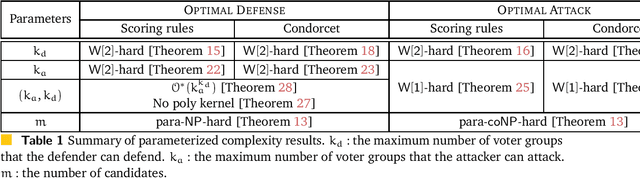
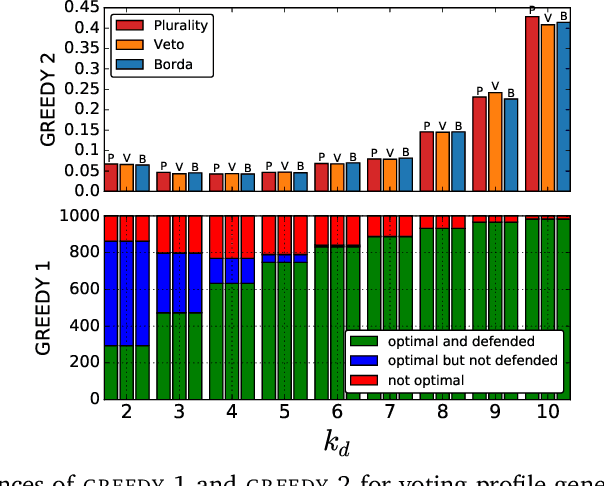
We study the parameterized complexity of the optimal defense and optimal attack problems in voting. In both the problems, the input is a set of voter groups (every voter group is a set of votes) and two integers $k_a$ and $k_d$ corresponding to respectively the number of voter groups the attacker can attack and the number of voter groups the defender can defend. A voter group gets removed from the election if it is attacked but not defended. In the optimal defense problem, we want to know if it is possible for the defender to commit to a strategy of defending at most $k_d$ voter groups such that, no matter which $k_a$ voter groups the attacker attacks, the outcome of the election does not change. In the optimal attack problem, we want to know if it is possible for the attacker to commit to a strategy of attacking $k_a$ voter groups such that, no matter which $k_d$ voter groups the defender defends, the outcome of the election is always different from the original (without any attack) one.

Testing Preferential Domains Using Sampling

A preferential domain is a collection of sets of preferences which are linear orders over a set of alternatives. These domains have been studied extensively in social choice theory due to both its practical importance and theoretical elegance. Examples of some extensively studied preferential domains include single peaked, single crossing, Euclidean, etc. In this paper, we study the sample complexity of testing whether a given preference profile is close to some specific domain. We consider two notions of closeness: (a) closeness via preferences, and (b) closeness via alternatives. We further explore the effect of assuming that the {\em outlier} preferences/alternatives to be random (instead of arbitrary) on the sample complexity of the testing problem. In most cases, we show that the above testing problem can be solved with high probability for all commonly used domains by observing only a small number of samples (independent of the number of preferences, $n$, and often the number of alternatives, $m$). In the remaining few cases, we prove either impossibility results or $\Omega(n)$ lower bound on the sample complexity. We complement our theoretical findings with extensive simulations to figure out the actual constant factors of our asymptotic sample complexity bounds.

Optimal Bribery in Voting

Studying complexity of various bribery problems has been one of the main research focus in computational social choice. In all the models of bribery studied so far, the briber has to pay every voter some amount of money depending on what the briber wants the voter to report and the briber has some budget at her disposal. Although these models successfully capture many real world applications, in many other scenarios, the voters may be unwilling to deviate too much from their true preferences. In this paper, we study the computational complexity of the problem of finding a preference profile which is as close to the true preference profile as possible and still achieves the briber's goal subject to budget constraints. We call this problem Optimal Bribery. We consider three important measures of distances, namely, swap distance, footrule distance, and maximum displacement distance, and resolve the complexity of the optimal bribery problem for many common voting rules. We show that the problem is polynomial time solvable for the plurality and veto voting rules for all the three measures of distance. On the other hand, we prove that the problem is NP-complete for a class of scoring rules which includes the Borda voting rule, maximin, Copeland$^\alpha$ for any $\alpha\in[0,1]$, and Bucklin voting rules for all the three measures of distance even when the distance allowed per voter is $1$ for the swap and maximum displacement distances and $2$ for the footrule distance even without the budget constraints (which corresponds to having an infinite budget). For the $k$-approval voting rule for any constant $k>1$ and the simplified Bucklin voting rule, we show that the problem is NP-complete for the swap distance even when the distance allowed is $2$ and for the footrule distance even when the distance allowed is $4$ even without the budget constraints.

Complexity of Manipulation with Partial Information in Voting

The Coalitional Manipulation problem has been studied extensively in the literature for many voting rules. However, most studies have focused on the complete information setting, wherein the manipulators know the votes of the non-manipulators. While this assumption is reasonable for purposes of showing intractability, it is unrealistic for algorithmic considerations. In most real-world scenarios, it is impractical for the manipulators to have accurate knowledge of all the other votes. In this paper, we investigate manipulation with incomplete information. In our framework, the manipulators know a partial order for each voter that is consistent with the true preference of that voter. In this setting, we formulate three natural computational notions of manipulation, namely weak, opportunistic, and strong manipulation. We say that an extension of a partial order is if there exists a manipulative vote for that extension. 1. Weak Manipulation (WM): the manipulators seek to vote in a way that makes their preferred candidate win in at least one extension of the partial votes of the non-manipulators. 2. Opportunistic Manipulation (OM): the manipulators seek to vote in a way that makes their preferred candidate win in every viable extension of the partial votes of the non-manipulators. 3. Strong Manipulation (SM): the manipulators seek to vote in a way that makes their preferred candidate win in every extension of the partial votes of the non-manipulators. We consider several scenarios for which the traditional manipulation problems are easy (for instance, Borda with a single manipulator). For many of them, the corresponding manipulative questions that we propose turn out to be computationally intractable. Our hardness results often hold even when very little information is missing, or in other words, even when the instances are quite close to the complete information setting.