Beyond $\tilde{O}(\sqrt{T})$ Constraint Violation for Online Convex Optimization with Adversarial Constraints

We revisit the Online Convex Optimization problem with adversarial constraints (COCO) where, in each round, a learner is presented with a convex cost function and a convex constraint function, both of which may be chosen adversarially. The learner selects actions from a convex decision set in an online fashion, with the goal of minimizing both regret and the cumulative constraint violation (CCV) over a horizon of $T$ rounds. The best-known policy for this problem achieves $O(\sqrt{T})$ regret and $\tilde{O}(\sqrt{T})$ CCV. In this paper, we present a surprising improvement that achieves a significantly smaller CCV by trading it off with regret. Specifically, for any bounded convex cost and constraint functions, we propose an online policy that achieves $\tilde{O}(\sqrt{dT}+ T^\beta)$ regret and $\tilde{O}(dT^{1-\beta})$ CCV, where $d$ is the dimension of the decision set and $\beta \in [0,1]$ is a tunable parameter. We achieve this result by first considering the special case of $\textsf{Constrained Expert}$ problem where the decision set is a probability simplex and the cost and constraint functions are linear. Leveraging a new adaptive small-loss regret bound, we propose an efficient policy for the $\textsf{Constrained Expert}$ problem, that attains $O(\sqrt{T\ln N}+T^{\beta})$ regret and $\tilde{O}(T^{1-\beta} \ln N)$ CCV, where $N$ is the number of experts. The original problem is then reduced to the $\textsf{Constrained Expert}$ problem via a covering argument. Finally, with an additional smoothness assumption, we propose an efficient gradient-based policy attaining $O(T^{\max(\frac{1}{2},\beta)})$ regret and $\tilde{O}(T^{1-\beta})$ CCV.

Online Bidding Algorithms with Strict Return on Spend (ROS) Constraint

Auto-bidding problem under a strict return-on-spend constraint (ROSC) is considered, where an algorithm has to make decisions about how much to bid for an ad slot depending on the revealed value, and the hidden allocation and payment function that describes the probability of winning the ad-slot depending on its bid. The objective of an algorithm is to maximize the expected utility (product of ad value and probability of winning the ad slot) summed across all time slots subject to the total expected payment being less than the total expected utility, called the ROSC. A (surprising) impossibility result is derived that shows that no online algorithm can achieve a sub-linear regret even when the value, allocation and payment function are drawn i.i.d. from an unknown distribution. The problem is non-trivial even when the revealed value remains constant across time slots, and an algorithm with regret guarantee that is optimal up to logarithmic factor is derived.

$O(\sqrt{T})$ Static Regret and Instance Dependent Constraint Violation for Constrained Online Convex Optimization

The constrained version of the standard online convex optimization (OCO) framework, called COCO is considered, where on every round, a convex cost function and a convex constraint function are revealed to the learner after it chooses the action for that round. The objective is to simultaneously minimize the static regret and cumulative constraint violation (CCV). An algorithm is proposed that guarantees a static regret of $O(\sqrt{T})$ and a CCV of $\min\{\cV, O(\sqrt{T}\log T) \}$, where $\cV$ depends on the distance between the consecutively revealed constraint sets, the shape of constraint sets, dimension of action space and the diameter of the action space. For special cases of constraint sets, $\cV=O(1)$. Compared to the state of the art results, static regret of $O(\sqrt{T})$ and CCV of $O(\sqrt{T}\log T)$, that were universal, the new result on CCV is instance dependent, which is derived by exploiting the geometric properties of the constraint sets.

Projection-free Algorithms for Online Convex Optimization with Adversarial Constraints

We study a generalization of the Online Convex Optimization (OCO) framework with time-varying adversarial constraints. In this problem, after selecting a feasible action from the convex decision set $X,$ a convex constraint function is revealed alongside the cost function in each round. Our goal is to design a computationally efficient learning policy that achieves a small regret with respect to the cost functions and a small cumulative constraint violation (CCV) with respect to the constraint functions over a horizon of length $T$. It is well-known that the projection step constitutes the major computational bottleneck of the standard OCO algorithms. However, for many structured decision sets, linear functions can be efficiently optimized over the decision set. We propose a *projection-free* online policy which makes a single call to a Linear Program (LP) solver per round. Our method outperforms state-of-the-art projection-free online algorithms with adversarial constraints, achieving improved bounds of $\tilde{O}(T^{\frac{3}{4}})$ for both regret and CCV. The proposed algorithm is conceptually simple - it first constructs a surrogate cost function as a non-negative linear combination of the cost and constraint functions. Then, it passes the surrogate costs to a new, adaptive version of the online conditional gradient subroutine, which we propose in this paper.

Tight Bounds for Online Convex Optimization with Adversarial Constraints

A well-studied generalization of the standard online convex optimization (OCO) is constrained online convex optimization (COCO). In COCO, on every round, a convex cost function and a convex constraint function are revealed to the learner after the action for that round is chosen. The objective is to design an online policy that simultaneously achieves a small regret while ensuring small cumulative constraint violation (CCV) against an adaptive adversary. A long-standing open question in COCO is whether an online policy can simultaneously achieve $O(\sqrt{T})$ regret and $O(\sqrt{T})$ CCV without any restrictive assumptions. For the first time, we answer this in the affirmative and show that an online policy can simultaneously achieve $O(\sqrt{T})$ regret and $\tilde{O}(\sqrt{T})$ CCV. We establish this result by effectively combining the adaptive regret bound of the AdaGrad algorithm with Lyapunov optimization - a classic tool from control theory. Surprisingly, the analysis is short and elegant.

Zero-shot Active Learning Using Self Supervised Learning

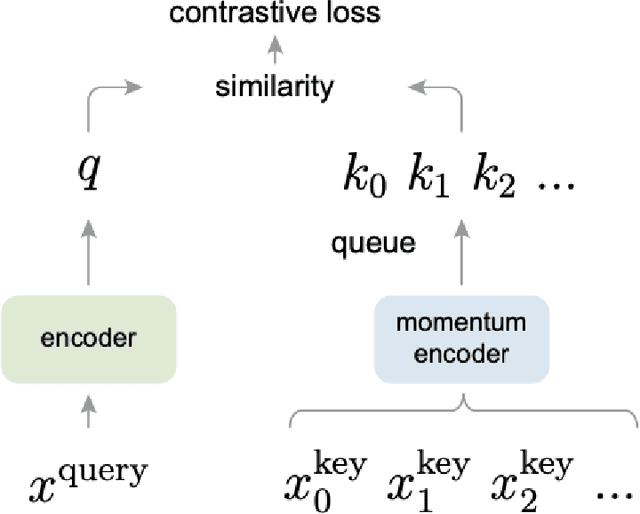
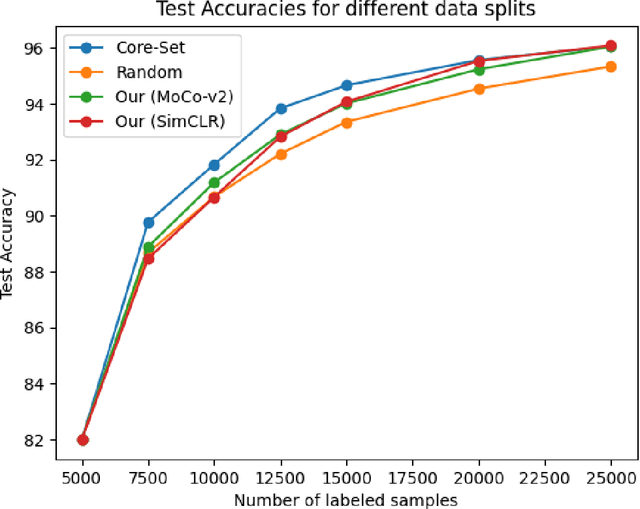
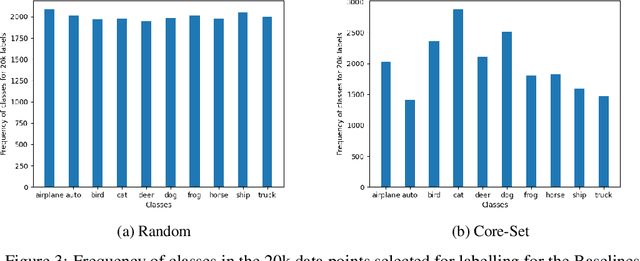
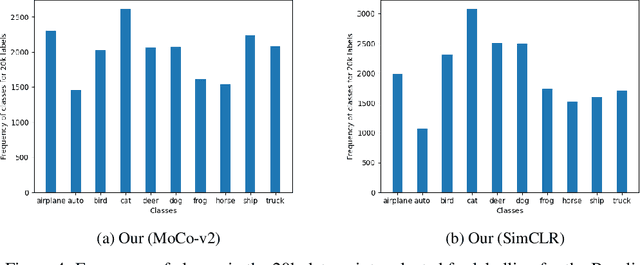
Deep learning algorithms are often said to be data hungry. The performance of such algorithms generally improve as more and more annotated data is fed into the model. While collecting unlabelled data is easier (as they can be scraped easily from the internet), annotating them is a tedious and expensive task. Given a fixed budget available for data annotation, Active Learning helps selecting the best subset of data for annotation, such that the deep learning model when trained over that subset will have maximum generalization performance under this budget. In this work, we aim to propose a new Active Learning approach which is model agnostic as well as one doesn't require an iterative process. We aim to leverage self-supervised learnt features for the task of Active Learning. The benefit of self-supervised learning, is that one can get useful feature representation of the input data, without having any annotation.

Confidence Is All You Need for MI Attacks

In this evolving era of machine learning security, membership inference attacks have emerged as a potent threat to the confidentiality of sensitive data. In this attack, adversaries aim to determine whether a particular point was used during the training of a target model. This paper proposes a new method to gauge a data point's membership in a model's training set. Instead of correlating loss with membership, as is traditionally done, we have leveraged the fact that training examples generally exhibit higher confidence values when classified into their actual class. During training, the model is essentially being 'fit' to the training data and might face particular difficulties in generalization to unseen data. This asymmetry leads to the model achieving higher confidence on the training data as it exploits the specific patterns and noise present in the training data. Our proposed approach leverages the confidence values generated by the machine learning model. These confidence values provide a probabilistic measure of the model's certainty in its predictions and can further be used to infer the membership of a given data point. Additionally, we also introduce another variant of our method that allows us to carry out this attack without knowing the ground truth(true class) of a given data point, thus offering an edge over existing label-dependent attack methods.

Playing in the Dark: No-regret Learning with Adversarial Constraints

We study a generalization of the classic Online Convex Optimization (OCO) framework by considering additional long-term adversarial constraints. Specifically, after an online policy decides its action on a round, in addition to a convex cost function, the adversary also reveals a set of $k$ convex constraints. The cost and the constraint functions could change arbitrarily with time, and no information about the future functions is assumed to be available. In this paper, we propose a meta-policy that simultaneously achieves a sublinear cumulative constraint violation and a sublinear regret. This is achieved via a black box reduction of the constrained problem to the standard OCO problem for a recursively constructed sequence of surrogate cost functions. We show that optimal performance bounds can be achieved by solving the surrogate problem using any adaptive OCO policy enjoying a standard data-dependent regret bound. A new Lyapunov-based proof technique is presented that reveals a connection between regret and certain sequential inequalities through a novel decomposition result. We conclude the paper by highlighting applications to online multi-task learning and network control problems.

$α$-Fair Contextual Bandits

Contextual bandit algorithms are at the core of many applications, including recommender systems, clinical trials, and optimal portfolio selection. One of the most popular problems studied in the contextual bandit literature is to maximize the sum of the rewards in each round by ensuring a sublinear regret against the best-fixed context-dependent policy. However, in many applications, the cumulative reward is not the right objective - the bandit algorithm must be fair in order to avoid the echo-chamber effect and comply with the regulatory requirements. In this paper, we consider the $\alpha$-Fair Contextual Bandits problem, where the objective is to maximize the global $\alpha$-fair utility function - a non-decreasing concave function of the cumulative rewards in the adversarial setting. The problem is challenging due to the non-separability of the objective across rounds. We design an efficient algorithm that guarantees an approximately sublinear regret in the full-information and bandit feedback settings.

BanditQ -- No-Regret Learning with Guaranteed Per-User Rewards in Adversarial Environments

Classic online prediction algorithms, such as Hedge, are inherently unfair by design, as they try to play the most rewarding arm as many times as possible while ignoring the sub-optimal arms to achieve sublinear regret. In this paper, we consider a fair online prediction problem in the adversarial setting with hard lower bounds on the rate of accrual of rewards for all arms. By combining elementary queueing theory with online learning, we propose a new online prediction policy, called BanditQ, that achieves the target rate constraints while achieving a regret of $O(T^{3/4})$ in the full-information setting. The design and analysis of BanditQ involve a novel use of the potential function method and are of independent interest.