Tight Bounds for Online Convex Optimization with Adversarial Constraints

A well-studied generalization of the standard online convex optimization (OCO) is constrained online convex optimization (COCO). In COCO, on every round, a convex cost function and a convex constraint function are revealed to the learner after the action for that round is chosen. The objective is to design an online policy that simultaneously achieves a small regret while ensuring small cumulative constraint violation (CCV) against an adaptive adversary. A long-standing open question in COCO is whether an online policy can simultaneously achieve $O(\sqrt{T})$ regret and $O(\sqrt{T})$ CCV without any restrictive assumptions. For the first time, we answer this in the affirmative and show that an online policy can simultaneously achieve $O(\sqrt{T})$ regret and $\tilde{O}(\sqrt{T})$ CCV. We establish this result by effectively combining the adaptive regret bound of the AdaGrad algorithm with Lyapunov optimization - a classic tool from control theory. Surprisingly, the analysis is short and elegant.

Capacity Provisioning Motivated Online Non-Convex Optimization Problem with Memory and Switching Cost

An online non-convex optimization problem is considered where the goal is to minimize the flow time (total delay) of a set of jobs by modulating the number of active servers, but with a switching cost associated with changing the number of active servers over time. Each job can be processed by at most one fixed speed server at any time. Compared to the usual online convex optimization (OCO) problem with switching cost, the objective function considered is non-convex and more importantly, at each time, it depends on all past decisions and not just the present one. Both worst-case and stochastic inputs are considered; for both cases, competitive algorithms are derived.

Playing in the Dark: No-regret Learning with Adversarial Constraints

We study a generalization of the classic Online Convex Optimization (OCO) framework by considering additional long-term adversarial constraints. Specifically, after an online policy decides its action on a round, in addition to a convex cost function, the adversary also reveals a set of $k$ convex constraints. The cost and the constraint functions could change arbitrarily with time, and no information about the future functions is assumed to be available. In this paper, we propose a meta-policy that simultaneously achieves a sublinear cumulative constraint violation and a sublinear regret. This is achieved via a black box reduction of the constrained problem to the standard OCO problem for a recursively constructed sequence of surrogate cost functions. We show that optimal performance bounds can be achieved by solving the surrogate problem using any adaptive OCO policy enjoying a standard data-dependent regret bound. A new Lyapunov-based proof technique is presented that reveals a connection between regret and certain sequential inequalities through a novel decomposition result. We conclude the paper by highlighting applications to online multi-task learning and network control problems.

Online Convex Optimization with Switching Cost and Delayed Gradients

We consider the online convex optimization (OCO) problem with quadratic and linear switching cost in the limited information setting, where an online algorithm can choose its action using only gradient information about the previous objective function. For $L$-smooth and $\mu$-strongly convex objective functions, we propose an online multiple gradient descent (OMGD) algorithm and show that its competitive ratio for the OCO problem with quadratic switching cost is at most $4(L + 5) + \frac{16(L + 5)}{\mu}$. The competitive ratio upper bound for OMGD is also shown to be order-wise tight in terms of $L,\mu$. In addition, we show that the competitive ratio of any online algorithm is $\max\{\Omega(L), \Omega(\frac{L}{\sqrt{\mu}})\}$ in the limited information setting when the switching cost is quadratic. We also show that the OMGD algorithm achieves the optimal (order-wise) dynamic regret in the limited information setting. For the linear switching cost, the competitive ratio upper bound of the OMGD algorithm is shown to depend on both the path length and the squared path length of the problem instance, in addition to $L, \mu$, and is shown to be order-wise, the best competitive ratio any online algorithm can achieve. Consequently, we conclude that the optimal competitive ratio for the quadratic and linear switching costs are fundamentally different in the limited information setting.

On Dynamic Regret and Constraint Violations in Constrained Online Convex Optimization

A constrained version of the online convex optimization (OCO) problem is considered. With slotted time, for each slot, first an action is chosen. Subsequently the loss function and the constraint violation penalty evaluated at the chosen action point is revealed. For each slot, both the loss function as well as the function defining the constraint set is assumed to be smooth and strongly convex. In addition, once an action is chosen, local information about a feasible set within a small neighborhood of the current action is also revealed. An algorithm is allowed to compute at most one gradient at its point of choice given the described feedback to choose the next action. The goal of an algorithm is to simultaneously minimize the dynamic regret (loss incurred compared to the oracle's loss) and the constraint violation penalty (penalty accrued compared to the oracle's penalty). We propose an algorithm that follows projected gradient descent over a suitably chosen set around the current action. We show that both the dynamic regret and the constraint violation is order-wise bounded by the {\it path-length}, the sum of the distances between the consecutive optimal actions. Moreover, we show that the derived bounds are the best possible.

Continuous Time Bandits With Sampling Costs

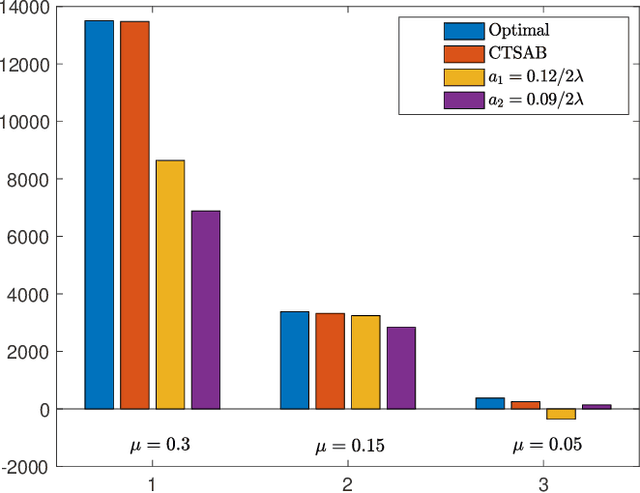
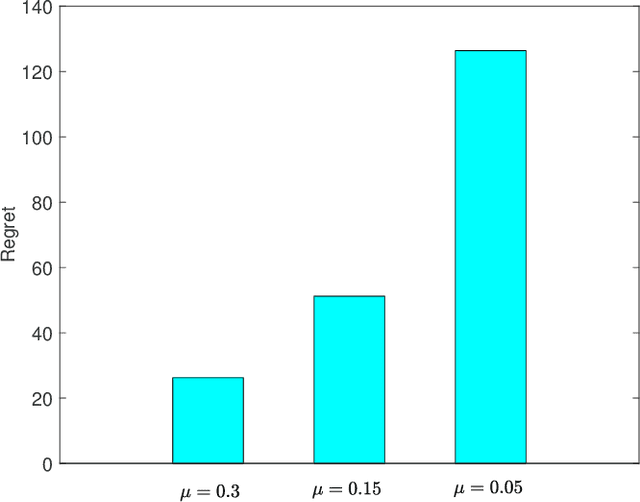
We consider a continuous-time multi-arm bandit problem (CTMAB), where the learner can sample arms any number of times in a given interval and obtain a random reward from each sample, however, increasing the frequency of sampling incurs an additive penalty/cost. Thus, there is a tradeoff between obtaining large reward and incurring sampling cost as a function of the sampling frequency. The goal is to design a learning algorithm that minimizes regret, that is defined as the difference of the payoff of the oracle policy and that of the learning algorithm. CTMAB is fundamentally different than the usual multi-arm bandit problem (MAB), e.g., even the single-arm case is non-trivial in CTMAB, since the optimal sampling frequency depends on the mean of the arm, which needs to be estimated. We first establish lower bounds on the regret achievable with any algorithm and then propose algorithms that achieve the lower bound up to logarithmic factors. For the single-arm case, we show that the lower bound on the regret is $\Omega((\log T)^2/\mu)$, where $\mu$ is the mean of the arm, and $T$ is the time horizon. For the multiple arms case, we show that the lower bound on the regret is $\Omega((\log T)^2 \mu/\Delta^2)$, where $\mu$ now represents the mean of the best arm, and $\Delta$ is the difference of the mean of the best and the second-best arm. We then propose an algorithm that achieves the bound up to constant terms.