When Online Algorithms Influence the Environment: A Dynamical Systems Analysis of the Unintended Consequences

We analyze the effect that online algorithms have on the environment that they are learning. As a motivation, consider recommendation systems that use online algorithms to learn optimal product recommendations based on user and product attributes. It is well known that the sequence of recommendations affects user preferences. However, typical learning algorithms treat the user attributes as static and disregard the impact of their recommendations on user preferences. Our interest is to analyze the effect of this mismatch between the model assumption of a static environment, and the reality of an evolving environment affected by the recommendations. To perform this analysis, we first introduce a model for a generic coupled evolution of the parameters that are being learned, and the environment that is affected by it. We then frame a linear bandit recommendation system (RS) into this generic model where the users are characterized by a state variable that evolves based on the sequence of recommendations. The learning algorithm of the RS does not explicitly account for this evolution and assumes that the users are static. A dynamical system model that captures the coupled evolution of the population state and the learning algorithm is described, and its equilibrium behavior is analyzed. We show that when the recommendation algorithm is able to learn the population preferences in the presence of this mismatch, the algorithm induces similarity in the preferences of the user population. In particular, we present results on how different properties of the recommendation algorithm, namely the user attribute space and the exploration-exploitation tradeoff, effect the population preferences when they are learned by the algorithm. We demonstrate these results using model simulations.

Representative Arm Identification: A fixed confidence approach to identify cluster representatives

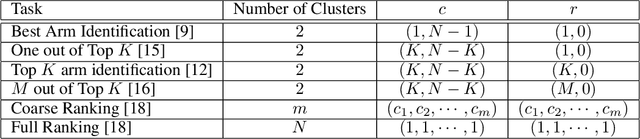
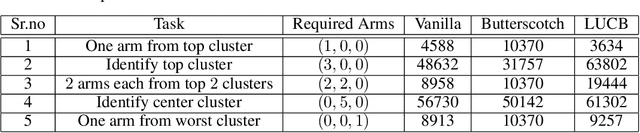
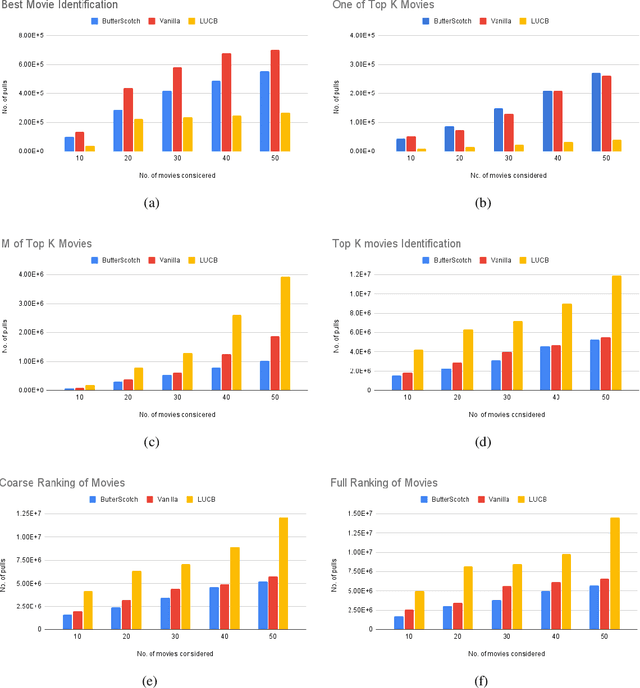
We study the representative arm identification (RAI) problem in the multi-armed bandits (MAB) framework, wherein we have a collection of arms, each associated with an unknown reward distribution. An underlying instance is defined by a partitioning of the arms into clusters of predefined sizes, such that for any $j > i$, all arms in cluster $i$ have a larger mean reward than those in cluster $j$. The goal in RAI is to reliably identify a certain prespecified number of arms from each cluster, while using as few arm pulls as possible. The RAI problem covers as special cases several well-studied MAB problems such as identifying the best arm or any $M$ out of the top $K$, as well as both full and coarse ranking. We start by providing an instance-dependent lower bound on the sample complexity of any feasible algorithm for this setting. We then propose two algorithms, based on the idea of confidence intervals, and provide high probability upper bounds on their sample complexity, which orderwise match the lower bound. Finally, we do an empirical comparison of both algorithms along with an LUCB-type alternative on both synthetic and real-world datasets, and demonstrate the superior performance of our proposed schemes in most cases.

Capacity Provisioning Motivated Online Non-Convex Optimization Problem with Memory and Switching Cost

An online non-convex optimization problem is considered where the goal is to minimize the flow time (total delay) of a set of jobs by modulating the number of active servers, but with a switching cost associated with changing the number of active servers over time. Each job can be processed by at most one fixed speed server at any time. Compared to the usual online convex optimization (OCO) problem with switching cost, the objective function considered is non-convex and more importantly, at each time, it depends on all past decisions and not just the present one. Both worst-case and stochastic inputs are considered; for both cases, competitive algorithms are derived.

Best Arm Identification in Bandits with Limited Precision Sampling

We study best arm identification in a variant of the multi-armed bandit problem where the learner has limited precision in arm selection. The learner can only sample arms via certain exploration bundles, which we refer to as boxes. In particular, at each sampling epoch, the learner selects a box, which in turn causes an arm to get pulled as per a box-specific probability distribution. The pulled arm and its instantaneous reward are revealed to the learner, whose goal is to find the best arm by minimising the expected stopping time, subject to an upper bound on the error probability. We present an asymptotic lower bound on the expected stopping time, which holds as the error probability vanishes. We show that the optimal allocation suggested by the lower bound is, in general, non-unique and therefore challenging to track. We propose a modified tracking-based algorithm to handle non-unique optimal allocations, and demonstrate that it is asymptotically optimal. We also present non-asymptotic lower and upper bounds on the stopping time in the simpler setting when the arms accessible from one box do not overlap with those of others.

Constrained Pure Exploration Multi-Armed Bandits with a Fixed Budget

We consider a constrained, pure exploration, stochastic multi-armed bandit formulation under a fixed budget. Each arm is associated with an unknown, possibly multi-dimensional distribution and is described by multiple attributes that are a function of this distribution. The aim is to optimize a particular attribute subject to user-defined constraints on the other attributes. This framework models applications such as financial portfolio optimization, where it is natural to perform risk-constrained maximization of mean return. We assume that the attributes can be estimated using samples from the arms' distributions and that these estimators satisfy suitable concentration inequalities. We propose an algorithm called \textsc{Constrained-SR} based on the Successive Rejects framework, which recommends an optimal arm and flags the instance as being feasible or infeasible. A key feature of this algorithm is that it is designed on the basis of an information theoretic lower bound for two-armed instances. We characterize an instance-dependent upper bound on the probability of error under \textsc{Constrained-SR}, that decays exponentially with respect to the budget. We further show that the associated decay rate is nearly optimal relative to an information theoretic lower bound in certain special cases.

Unsupervised Crowdsourcing with Accuracy and Cost Guarantees

We consider the problem of cost-optimal utilization of a crowdsourcing platform for binary, unsupervised classification of a collection of items, given a prescribed error threshold. Workers on the crowdsourcing platform are assumed to be divided into multiple classes, based on their skill, experience, and/or past performance. We model each worker class via an unknown confusion matrix, and a (known) price to be paid per label prediction. For this setting, we propose algorithms for acquiring label predictions from workers, and for inferring the true labels of items. We prove that if the number of (unlabeled) items available is large enough, our algorithms satisfy the prescribed error thresholds, incurring a cost that is near-optimal. Finally, we validate our algorithms, and some heuristics inspired by them, through an extensive case study.

Sequential Community Mode Estimation

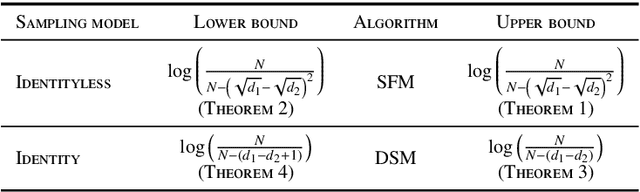
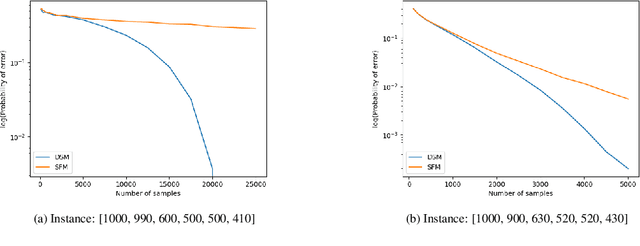
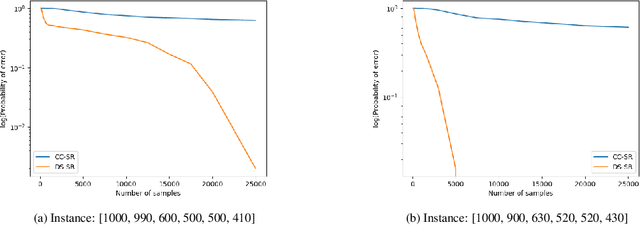
We consider a population, partitioned into a set of communities, and study the problem of identifying the largest community within the population via sequential, random sampling of individuals. There are multiple sampling domains, referred to as \emph{boxes}, which also partition the population. Each box may consist of individuals of different communities, and each community may in turn be spread across multiple boxes. The learning agent can, at any time, sample (with replacement) a random individual from any chosen box; when this is done, the agent learns the community the sampled individual belongs to, and also whether or not this individual has been sampled before. The goal of the agent is to minimize the probability of mis-identifying the largest community in a \emph{fixed budget} setting, by optimizing both the sampling strategy as well as the decision rule. We propose and analyse novel algorithms for this problem, and also establish information theoretic lower bounds on the probability of error under any algorithm. In several cases of interest, the exponential decay rates of the probability of error under our algorithms are shown to be optimal up to constant factors. The proposed algorithms are further validated via simulations on real-world datasets.

Optimal Cycling of a Heterogenous Battery Bank via Reinforcement Learning

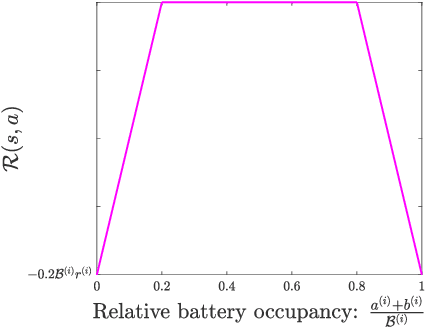
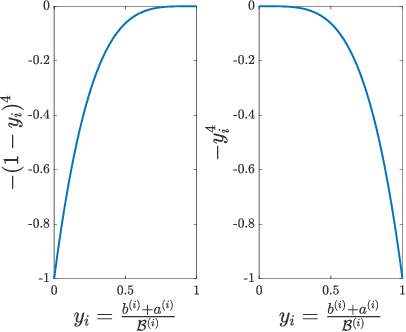
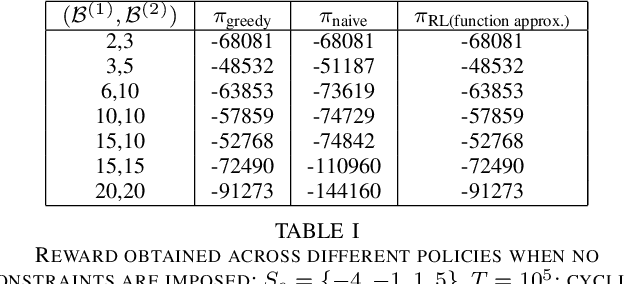
We consider the problem of optimal charging/discharging of a bank of heterogenous battery units, driven by stochastic electricity generation and demand processes. The batteries in the battery bank may differ with respect to their capacities, ramp constraints, losses, as well as cycling costs. The goal is to minimize the degradation costs associated with battery cycling in the long run; this is posed formally as a Markov decision process. We propose a linear function approximation based Q-learning algorithm for learning the optimal solution, using a specially designed class of kernel functions that approximate the structure of the value functions associated with the MDP. The proposed algorithm is validated via an extensive case study.

Statistically Robust, Risk-Averse Best Arm Identification in Multi-Armed Bandits

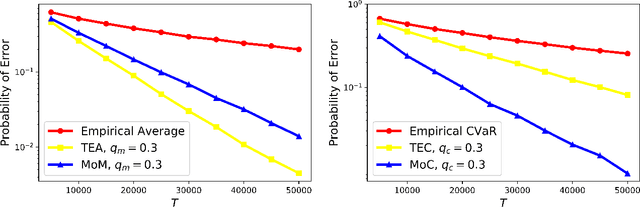
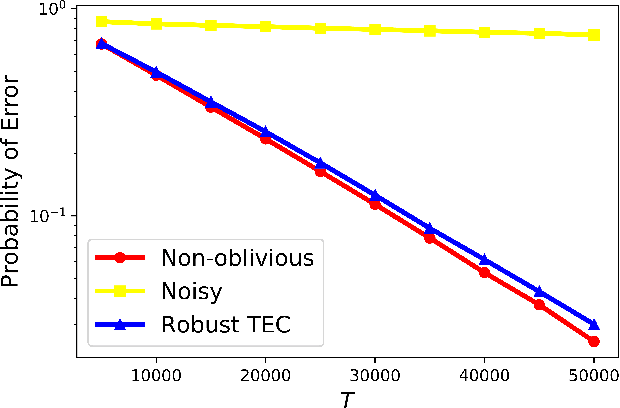
Traditional multi-armed bandit (MAB) formulations usually make certain assumptions about the underlying arms' distributions, such as bounds on the support or their tail behaviour. Moreover, such parametric information is usually 'baked' into the algorithms. In this paper, we show that specialized algorithms that exploit such parametric information are prone to inconsistent learning performance when the parameter is misspecified. Our key contributions are twofold: (i) We establish fundamental performance limits of statistically robust MAB algorithms under the fixed-budget pure exploration setting, and (ii) We propose two classes of algorithms that are asymptotically near-optimal. Additionally, we consider a risk-aware criterion for best arm identification, where the objective associated with each arm is a linear combination of the mean and the conditional value at risk (CVaR). Throughout, we make a very mild 'bounded moment' assumption, which lets us work with both light-tailed and heavy-tailed distributions within a unified framework.

Bandit algorithms: Letting go of logarithmic regret for statistical robustness

We study regret minimization in a stochastic multi-armed bandit setting and establish a fundamental trade-off between the regret suffered under an algorithm, and its statistical robustness. Considering broad classes of underlying arms' distributions, we show that bandit learning algorithms with logarithmic regret are always inconsistent and that consistent learning algorithms always suffer a super-logarithmic regret. This result highlights the inevitable statistical fragility of all `logarithmic regret' bandit algorithms available in the literature---for instance, if a UCB algorithm designed for $\sigma$-subGaussian distributions is used in a subGaussian setting with a mismatched variance parameter, the learning performance could be inconsistent. Next, we show a positive result: statistically robust and consistent learning performance is attainable if we allow the regret to be slightly worse than logarithmic. Specifically, we propose three classes of distribution oblivious algorithms that achieve an asymptotic regret that is arbitrarily close to logarithmic.