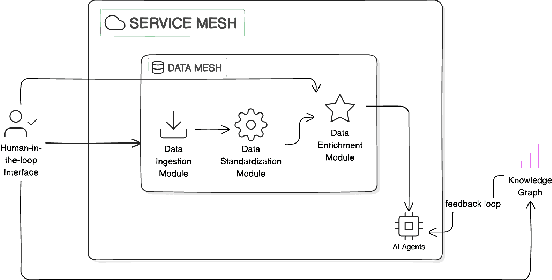
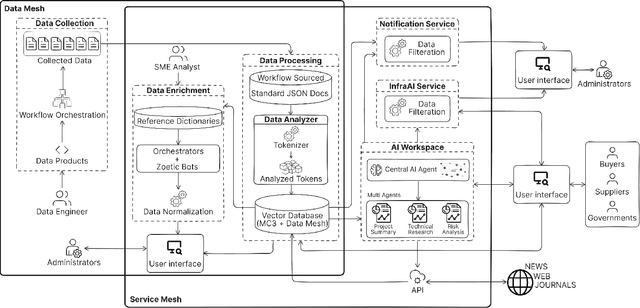
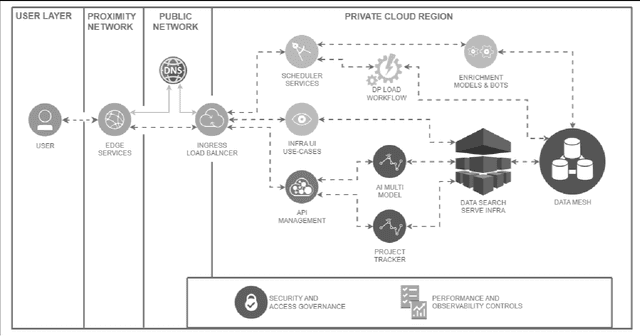
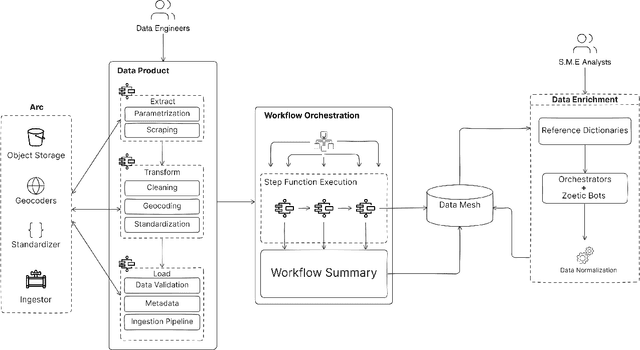
An AI-Driven Data Mesh Architecture Enhancing Decision-Making in Infrastructure Construction and Public Procurement

Infrastructure construction, often dubbed an "industry of industries," is closely linked with government spending and public procurement, offering significant opportunities for improved efficiency and productivity through better transparency and information access. By leveraging these opportunities, we can achieve notable gains in productivity, cost savings, and broader economic benefits. Our approach introduces an integrated software ecosystem utilizing Data Mesh and Service Mesh architectures. This system includes the largest training dataset for infrastructure and procurement, encompassing over 100 billion tokens, scientific publications, activities, and risk data, all structured by a systematic AI framework. Supported by a Knowledge Graph linked to domain-specific multi-agent tasks and Q&A capabilities, our platform standardizes and ingests diverse data sources, transforming them into structured knowledge. Leveraging large language models (LLMs) and automation, our system revolutionizes data structuring and knowledge creation, aiding decision-making in early-stage project planning, detailed research, market trend analysis, and qualitative assessments. Its web-scalable architecture delivers domain-curated information, enabling AI agents to facilitate reasoning and manage uncertainties, while preparing for future expansions with specialized agents targeting particular challenges. This integration of AI with domain expertise not only boosts efficiency and decision-making in construction and infrastructure but also establishes a framework for enhancing government efficiency and accelerating the transition of traditional industries to digital workflows. This work is poised to significantly influence AI-driven initiatives in this sector and guide best practices in AI Operations.

Representative Arm Identification: A fixed confidence approach to identify cluster representatives

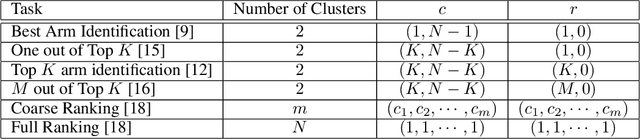
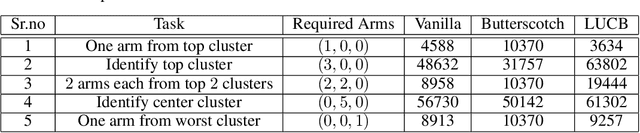
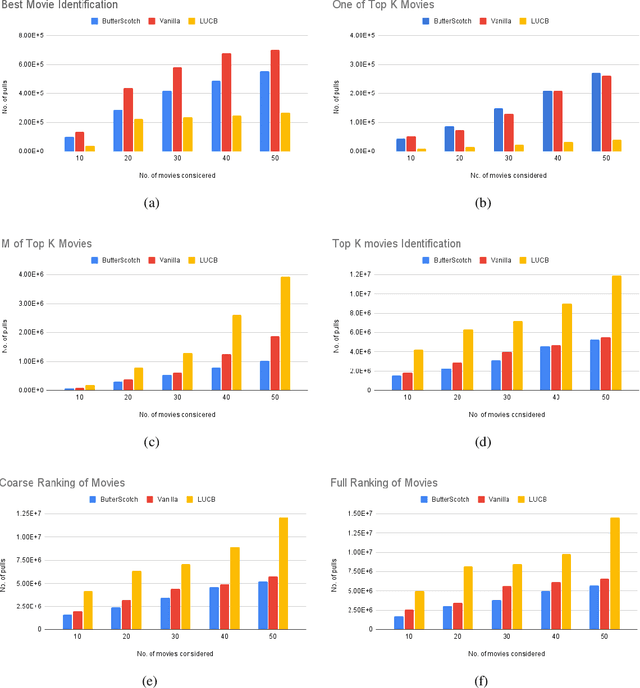
We study the representative arm identification (RAI) problem in the multi-armed bandits (MAB) framework, wherein we have a collection of arms, each associated with an unknown reward distribution. An underlying instance is defined by a partitioning of the arms into clusters of predefined sizes, such that for any $j > i$, all arms in cluster $i$ have a larger mean reward than those in cluster $j$. The goal in RAI is to reliably identify a certain prespecified number of arms from each cluster, while using as few arm pulls as possible. The RAI problem covers as special cases several well-studied MAB problems such as identifying the best arm or any $M$ out of the top $K$, as well as both full and coarse ranking. We start by providing an instance-dependent lower bound on the sample complexity of any feasible algorithm for this setting. We then propose two algorithms, based on the idea of confidence intervals, and provide high probability upper bounds on their sample complexity, which orderwise match the lower bound. Finally, we do an empirical comparison of both algorithms along with an LUCB-type alternative on both synthetic and real-world datasets, and demonstrate the superior performance of our proposed schemes in most cases.