Representative Arm Identification: A fixed confidence approach to identify cluster representatives
Paper and Code
Aug 26, 2024
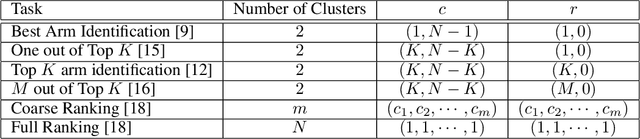
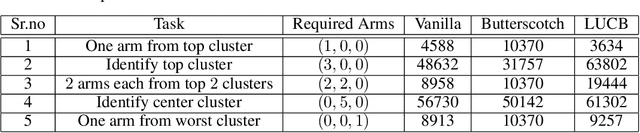
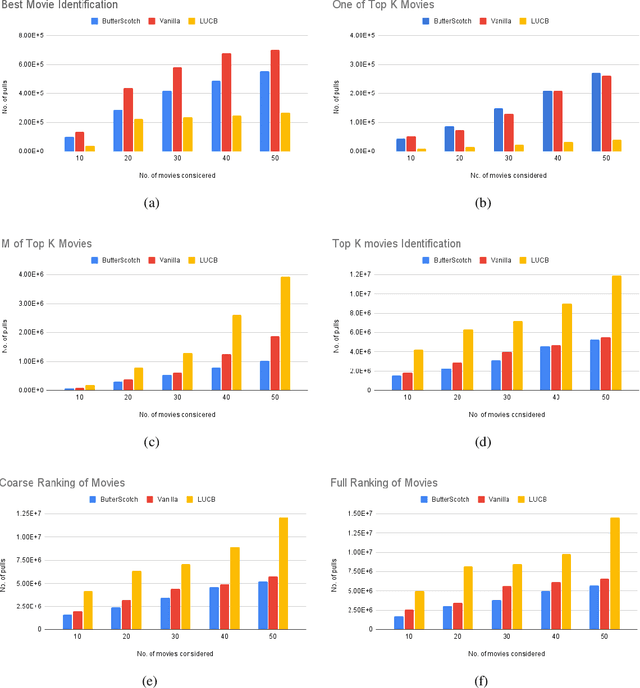
We study the representative arm identification (RAI) problem in the multi-armed bandits (MAB) framework, wherein we have a collection of arms, each associated with an unknown reward distribution. An underlying instance is defined by a partitioning of the arms into clusters of predefined sizes, such that for any $j > i$, all arms in cluster $i$ have a larger mean reward than those in cluster $j$. The goal in RAI is to reliably identify a certain prespecified number of arms from each cluster, while using as few arm pulls as possible. The RAI problem covers as special cases several well-studied MAB problems such as identifying the best arm or any $M$ out of the top $K$, as well as both full and coarse ranking. We start by providing an instance-dependent lower bound on the sample complexity of any feasible algorithm for this setting. We then propose two algorithms, based on the idea of confidence intervals, and provide high probability upper bounds on their sample complexity, which orderwise match the lower bound. Finally, we do an empirical comparison of both algorithms along with an LUCB-type alternative on both synthetic and real-world datasets, and demonstrate the superior performance of our proposed schemes in most cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge