Statistically Robust, Risk-Averse Best Arm Identification in Multi-Armed Bandits
Paper and Code
Aug 28, 2020

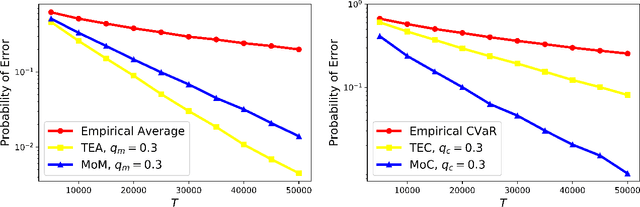
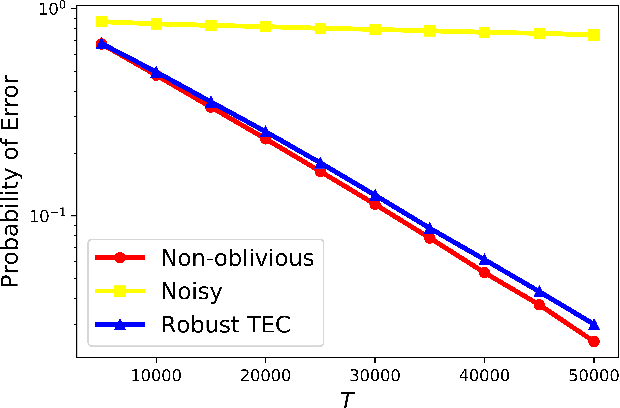
Traditional multi-armed bandit (MAB) formulations usually make certain assumptions about the underlying arms' distributions, such as bounds on the support or their tail behaviour. Moreover, such parametric information is usually 'baked' into the algorithms. In this paper, we show that specialized algorithms that exploit such parametric information are prone to inconsistent learning performance when the parameter is misspecified. Our key contributions are twofold: (i) We establish fundamental performance limits of statistically robust MAB algorithms under the fixed-budget pure exploration setting, and (ii) We propose two classes of algorithms that are asymptotically near-optimal. Additionally, we consider a risk-aware criterion for best arm identification, where the objective associated with each arm is a linear combination of the mean and the conditional value at risk (CVaR). Throughout, we make a very mild 'bounded moment' assumption, which lets us work with both light-tailed and heavy-tailed distributions within a unified framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge