Adaptive Crowdsourcing Via Self-Supervised Learning

Common crowdsourcing systems average estimates of a latent quantity of interest provided by many crowdworkers to produce a group estimate. We develop a new approach -- predict-each-worker -- that leverages self-supervised learning and a novel aggregation scheme. This approach adapts weights assigned to crowdworkers based on estimates they provided for previous quantities. When skills vary across crowdworkers or their estimates correlate, the weighted sum offers a more accurate group estimate than the average. Existing algorithms such as expectation maximization can, at least in principle, produce similarly accurate group estimates. However, their computational requirements become onerous when complex models, such as neural networks, are required to express relationships among crowdworkers. Predict-each-worker accommodates such complexity as well as many other practical challenges. We analyze the efficacy of predict-each-worker through theoretical and computational studies. Among other things, we establish asymptotic optimality as the number of engagements per crowdworker grows.

Statistically Robust, Risk-Averse Best Arm Identification in Multi-Armed Bandits

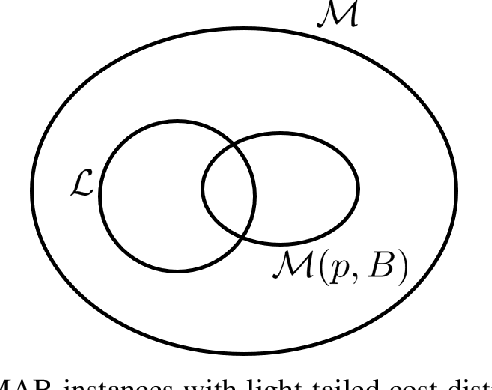
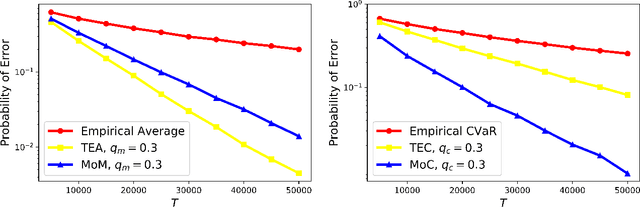
Traditional multi-armed bandit (MAB) formulations usually make certain assumptions about the underlying arms' distributions, such as bounds on the support or their tail behaviour. Moreover, such parametric information is usually 'baked' into the algorithms. In this paper, we show that specialized algorithms that exploit such parametric information are prone to inconsistent learning performance when the parameter is misspecified. Our key contributions are twofold: (i) We establish fundamental performance limits of statistically robust MAB algorithms under the fixed-budget pure exploration setting, and (ii) We propose two classes of algorithms that are asymptotically near-optimal. Additionally, we consider a risk-aware criterion for best arm identification, where the objective associated with each arm is a linear combination of the mean and the conditional value at risk (CVaR). Throughout, we make a very mild 'bounded moment' assumption, which lets us work with both light-tailed and heavy-tailed distributions within a unified framework.

Bandit algorithms: Letting go of logarithmic regret for statistical robustness

We study regret minimization in a stochastic multi-armed bandit setting and establish a fundamental trade-off between the regret suffered under an algorithm, and its statistical robustness. Considering broad classes of underlying arms' distributions, we show that bandit learning algorithms with logarithmic regret are always inconsistent and that consistent learning algorithms always suffer a super-logarithmic regret. This result highlights the inevitable statistical fragility of all `logarithmic regret' bandit algorithms available in the literature---for instance, if a UCB algorithm designed for $\sigma$-subGaussian distributions is used in a subGaussian setting with a mismatched variance parameter, the learning performance could be inconsistent. Next, we show a positive result: statistically robust and consistent learning performance is attainable if we allow the regret to be slightly worse than logarithmic. Specifically, we propose three classes of distribution oblivious algorithms that achieve an asymptotic regret that is arbitrarily close to logarithmic.

Constrained regret minimization for multi-criterion multi-armed bandits

We consider a stochastic multi-armed bandit setting and study the problem of regret minimization over a given time horizon, subject to a risk constraint. Each arm is associated with an unknown cost/loss distribution. The learning agent is characterized by a risk-appetite that she is willing to tolerate, which we model using a pre-specified upper bound on the Conditional Value at Risk (CVaR). An optimal arm is one that minimizes the expected loss, among those arms that satisfy the CVaR constraint. The agent is interested in minimizing the number of pulls of suboptimal arms, including the ones that are 'too risky.' For this problem, we propose a Risk-Constrained Lower Confidence Bound (RC-LCB) algorithm, that guarantees logarithmic regret, i.e., the average number of plays of all non-optimal arms is at most logarithmic in the horizon. The algorithm also outputs a boolean flag that correctly identifies with high probability, whether the given instance was feasible/infeasible with respect to the risk constraint. We prove lower bounds on the performance of any risk-constrained regret minimization algorithm and establish a fundamental trade-off between regret minimization and feasibility identification. The proposed algorithm and analyses can be readily generalized to solve constrained multi-criterion optimization problems in the bandits setting.

Distribution oblivious, risk-aware algorithms for multi-armed bandits with unbounded rewards

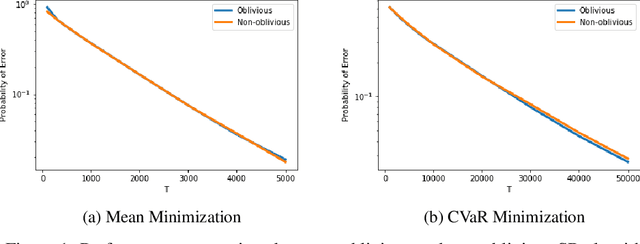
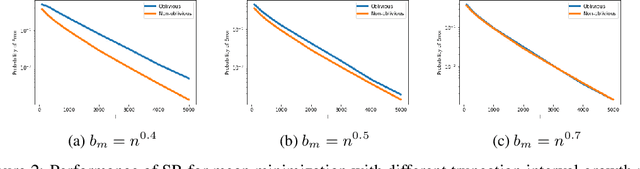
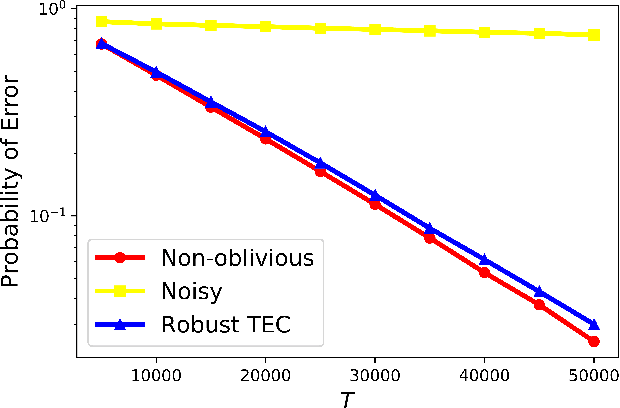
Classical multi-armed bandit problems use the expected value of an arm as a metric to evaluate its goodness. However, the expected value is a risk-neutral metric. In many applications like finance, one is interested in balancing the expected return of an arm (or portfolio) with the risk associated with that return. In this paper, we consider the problem of selecting the arm that optimizes a linear combination of the expected reward and the associated Conditional Value at Risk (CVaR) in a fixed budget best-arm identification framework. We allow the reward distributions to be unbounded or even heavy-tailed. For this problem, our goal is to devise algorithms that are entirely distribution oblivious, i.e., the algorithm is not aware of any information on the reward distributions, including bounds on the moments/tails, or the suboptimality gaps across arms. In this paper, we provide a class of such algorithms with provable upper bounds on the probability of incorrect identification. In the process, we develop a novel estimator for the CVaR of unbounded (including heavy-tailed) random variables and prove a concentration inequality for the same, which could be of independent interest. We also compare the error bounds for our distribution oblivious algorithms with those corresponding to standard non-oblivious algorithms. Finally, numerical experiments reveal that our algorithms perform competitively when compared with non-oblivious algorithms, suggesting that distribution obliviousness can be realised in practice without incurring a significant loss of performance.