Choice between Partial Trajectories

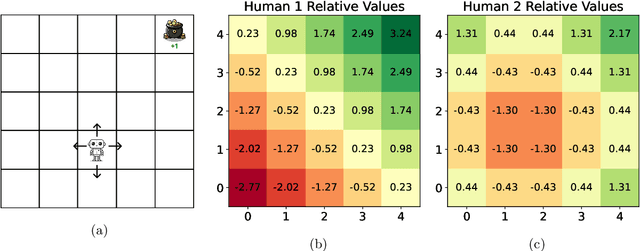
As AI agents generate increasingly sophisticated behaviors, manually encoding human preferences to guide these agents becomes more challenging. To address this, it has been suggested that agents instead learn preferences from human choice data. This approach requires a model of choice behavior that the agent can use to interpret the data. For choices between partial trajectories of states and actions, previous models assume choice probabilities to be determined by the partial return or the cumulative advantage. We consider an alternative model based instead on the bootstrapped return, which adds to the partial return an estimate of the future return. Benefits of the bootstrapped return model stem from its treatment of human beliefs. Unlike partial return, choices based on bootstrapped return reflect human beliefs about the environment. Further, while recovering the reward function from choices based on cumulative advantage requires that those beliefs are correct, doing so from choices based on bootstrapped return does not. To motivate the bootstrapped return model, we formulate axioms and prove an Alignment Theorem. This result formalizes how, for a general class of human preferences, such models are able to disentangle goals from beliefs. This ensures recovery of an aligned reward function when learning from choices based on bootstrapped return. The bootstrapped return model also affords greater robustness to choice behavior. Even when choices are based on partial return, learning via a bootstrapped return model recovers an aligned reward function. The same holds with choices based on the cumulative advantage if the human and the agent both adhere to correct and consistent beliefs about the environment. On the other hand, if choices are based on bootstrapped return, learning via partial return or cumulative advantage models does not generally produce an aligned reward function.

Aligning AI Agents via Information-Directed Sampling

The staggering feats of AI systems have brought to attention the topic of AI Alignment: aligning a "superintelligent" AI agent's actions with humanity's interests. Many existing frameworks/algorithms in alignment study the problem on a myopic horizon or study learning from human feedback in isolation, relying on the contrived assumption that the agent has already perfectly identified the environment. As a starting point to address these limitations, we define a class of bandit alignment problems as an extension of classic multi-armed bandit problems. A bandit alignment problem involves an agent tasked with maximizing long-run expected reward by interacting with an environment and a human, both involving details/preferences initially unknown to the agent. The reward of actions in the environment depends on both observed outcomes and human preferences. Furthermore, costs are associated with querying the human to learn preferences. Therefore, an effective agent ought to intelligently trade-off exploration (of the environment and human) and exploitation. We study these trade-offs theoretically and empirically in a toy bandit alignment problem which resembles the beta-Bernoulli bandit. We demonstrate while naive exploration algorithms which reflect current practices and even touted algorithms such as Thompson sampling both fail to provide acceptable solutions to this problem, information-directed sampling achieves favorable regret.

The Need for a Big World Simulator: A Scientific Challenge for Continual Learning

The "small agent, big world" frame offers a conceptual view that motivates the need for continual learning. The idea is that a small agent operating in a much bigger world cannot store all information that the world has to offer. To perform well, the agent must be carefully designed to ingest, retain, and eject the right information. To enable the development of performant continual learning agents, a number of synthetic environments have been proposed. However, these benchmarks suffer from limitations, including unnatural distribution shifts and a lack of fidelity to the "small agent, big world" framing. This paper aims to formalize two desiderata for the design of future simulated environments. These two criteria aim to reflect the objectives and complexity of continual learning in practical settings while enabling rapid prototyping of algorithms on a smaller scale.

Information-Theoretic Foundations for Machine Learning

The staggering progress of machine learning in the past decade has been a sight to behold. In retrospect, it is both remarkable and unsettling that these milestones were achievable with little to no rigorous theory to guide experimentation. Despite this fact, practitioners have been able to guide their future experimentation via observations from previous large-scale empirical investigations. However, alluding to Plato's Allegory of the cave, it is likely that the observations which form the field's notion of reality are but shadows representing fragments of that reality. In this work, we propose a theoretical framework which attempts to answer what exists outside of the cave. To the theorist, we provide a framework which is mathematically rigorous and leaves open many interesting ideas for future exploration. To the practitioner, we provide a framework whose results are very intuitive, general, and which will help form principles to guide future investigations. Concretely, we provide a theoretical framework rooted in Bayesian statistics and Shannon's information theory which is general enough to unify the analysis of many phenomena in machine learning. Our framework characterizes the performance of an optimal Bayesian learner, which considers the fundamental limits of information. Throughout this work, we derive very general theoretical results and apply them to derive insights specific to settings ranging from data which is independently and identically distributed under an unknown distribution, to data which is sequential, to data which exhibits hierarchical structure amenable to meta-learning. We conclude with a section dedicated to characterizing the performance of misspecified algorithms. These results are exciting and particularly relevant as we strive to overcome increasingly difficult machine learning challenges in this endlessly complex world.

Exploration Unbound

A sequential decision-making agent balances between exploring to gain new knowledge about an environment and exploiting current knowledge to maximize immediate reward. For environments studied in the traditional literature, optimal decisions gravitate over time toward exploitation as the agent accumulates sufficient knowledge and the benefits of further exploration vanish. What if, however, the environment offers an unlimited amount of useful knowledge and there is large benefit to further exploration no matter how much the agent has learned? We offer a simple, quintessential example of such a complex environment. In this environment, rewards are unbounded and an agent can always increase the rate at which rewards accumulate by exploring to learn more. Consequently, an optimal agent forever maintains a propensity to explore.

Satisficing Exploration for Deep Reinforcement Learning

A default assumption in the design of reinforcement-learning algorithms is that a decision-making agent always explores to learn optimal behavior. In sufficiently complex environments that approach the vastness and scale of the real world, however, attaining optimal performance may in fact be an entirely intractable endeavor and an agent may seldom find itself in a position to complete the requisite exploration for identifying an optimal policy. Recent work has leveraged tools from information theory to design agents that deliberately forgo optimal solutions in favor of sufficiently-satisfying or satisficing solutions, obtained through lossy compression. Notably, such agents may employ fundamentally different exploratory decisions to learn satisficing behaviors more efficiently than optimal ones that are more data intensive. While supported by a rigorous corroborating theory, the underlying algorithm relies on model-based planning, drastically limiting the compatibility of these ideas with function approximation and high-dimensional observations. In this work, we remedy this issue by extending an agent that directly represents uncertainty over the optimal value function allowing it to both bypass the need for model-based planning and to learn satisficing policies. We provide simple yet illustrative experiments that demonstrate how our algorithm enables deep reinforcement-learning agents to achieve satisficing behaviors. In keeping with previous work on this setting for multi-armed bandits, we additionally find that our algorithm is capable of synthesizing optimal behaviors, when feasible, more efficiently than its non-information-theoretic counterpart.

Information-Theoretic Foundations for Neural Scaling Laws

Neural scaling laws aim to characterize how out-of-sample error behaves as a function of model and training dataset size. Such scaling laws guide allocation of a computational resources between model and data processing to minimize error. However, existing theoretical support for neural scaling laws lacks rigor and clarity, entangling the roles of information and optimization. In this work, we develop rigorous information-theoretic foundations for neural scaling laws. This allows us to characterize scaling laws for data generated by a two-layer neural network of infinite width. We observe that the optimal relation between data and model size is linear, up to logarithmic factors, corroborating large-scale empirical investigations. Concise yet general results of the kind we establish may bring clarity to this topic and inform future investigations.

Adaptive Crowdsourcing Via Self-Supervised Learning

Common crowdsourcing systems average estimates of a latent quantity of interest provided by many crowdworkers to produce a group estimate. We develop a new approach -- predict-each-worker -- that leverages self-supervised learning and a novel aggregation scheme. This approach adapts weights assigned to crowdworkers based on estimates they provided for previous quantities. When skills vary across crowdworkers or their estimates correlate, the weighted sum offers a more accurate group estimate than the average. Existing algorithms such as expectation maximization can, at least in principle, produce similarly accurate group estimates. However, their computational requirements become onerous when complex models, such as neural networks, are required to express relationships among crowdworkers. Predict-each-worker accommodates such complexity as well as many other practical challenges. We analyze the efficacy of predict-each-worker through theoretical and computational studies. Among other things, we establish asymptotic optimality as the number of engagements per crowdworker grows.

Efficient Exploration for LLMs

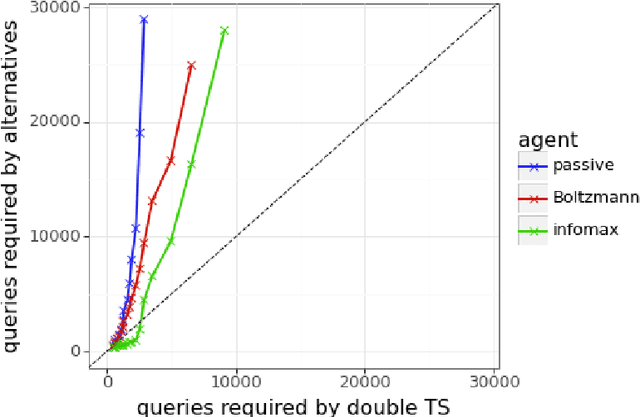
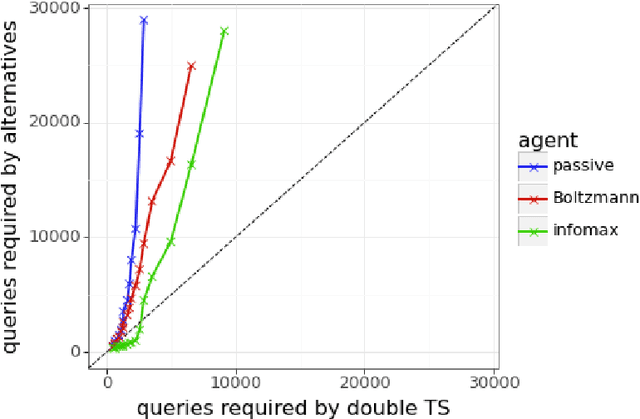
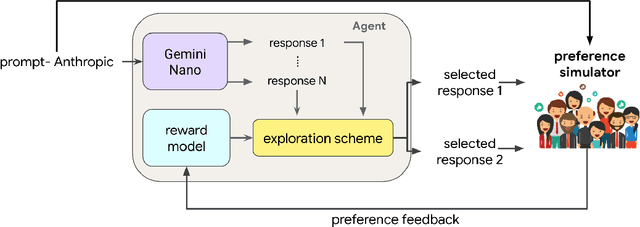
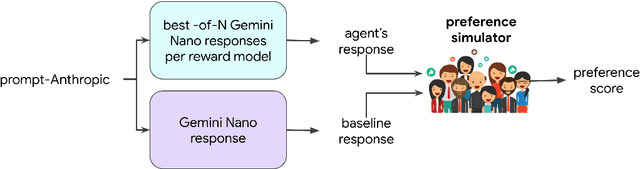
We present evidence of substantial benefit from efficient exploration in gathering human feedback to improve large language models. In our experiments, an agent sequentially generates queries while fitting a reward model to the feedback received. Our best-performing agent generates queries using double Thompson sampling, with uncertainty represented by an epistemic neural network. Our results demonstrate that efficient exploration enables high levels of performance with far fewer queries. Further, both uncertainty estimation and the choice of exploration scheme play critical roles.

An Information-Theoretic Analysis of In-Context Learning

Previous theoretical results pertaining to meta-learning on sequences build on contrived assumptions and are somewhat convoluted. We introduce new information-theoretic tools that lead to an elegant and very general decomposition of error into three components: irreducible error, meta-learning error, and intra-task error. These tools unify analyses across many meta-learning challenges. To illustrate, we apply them to establish new results about in-context learning with transformers. Our theoretical results characterizes how error decays in both the number of training sequences and sequence lengths. Our results are very general; for example, they avoid contrived mixing time assumptions made by all prior results that establish decay of error with sequence length.