Satisficing Exploration for Deep Reinforcement Learning

A default assumption in the design of reinforcement-learning algorithms is that a decision-making agent always explores to learn optimal behavior. In sufficiently complex environments that approach the vastness and scale of the real world, however, attaining optimal performance may in fact be an entirely intractable endeavor and an agent may seldom find itself in a position to complete the requisite exploration for identifying an optimal policy. Recent work has leveraged tools from information theory to design agents that deliberately forgo optimal solutions in favor of sufficiently-satisfying or satisficing solutions, obtained through lossy compression. Notably, such agents may employ fundamentally different exploratory decisions to learn satisficing behaviors more efficiently than optimal ones that are more data intensive. While supported by a rigorous corroborating theory, the underlying algorithm relies on model-based planning, drastically limiting the compatibility of these ideas with function approximation and high-dimensional observations. In this work, we remedy this issue by extending an agent that directly represents uncertainty over the optimal value function allowing it to both bypass the need for model-based planning and to learn satisficing policies. We provide simple yet illustrative experiments that demonstrate how our algorithm enables deep reinforcement-learning agents to achieve satisficing behaviors. In keeping with previous work on this setting for multi-armed bandits, we additionally find that our algorithm is capable of synthesizing optimal behaviors, when feasible, more efficiently than its non-information-theoretic counterpart.

Target Networks and Over-parameterization Stabilize Off-policy Bootstrapping with Function Approximation

We prove that the combination of a target network and over-parameterized linear function approximation establishes a weaker convergence condition for bootstrapped value estimation in certain cases, even with off-policy data. Our condition is naturally satisfied for expected updates over the entire state-action space or learning with a batch of complete trajectories from episodic Markov decision processes. Notably, using only a target network or an over-parameterized model does not provide such a convergence guarantee. Additionally, we extend our results to learning with truncated trajectories, showing that convergence is achievable for all tasks with minor modifications, akin to value truncation for the final states in trajectories. Our primary result focuses on temporal difference estimation for prediction, providing high-probability value estimation error bounds and empirical analysis on Baird's counterexample and a Four-room task. Furthermore, we explore the control setting, demonstrating that similar convergence conditions apply to Q-learning.

A Parametric Class of Approximate Gradient Updates for Policy Optimization

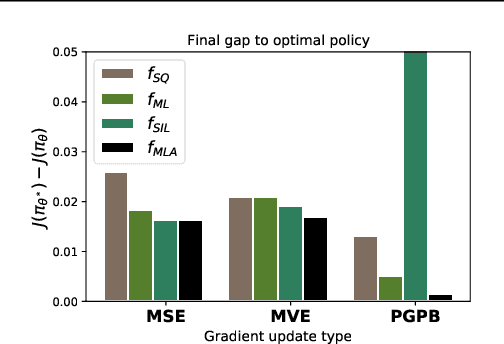
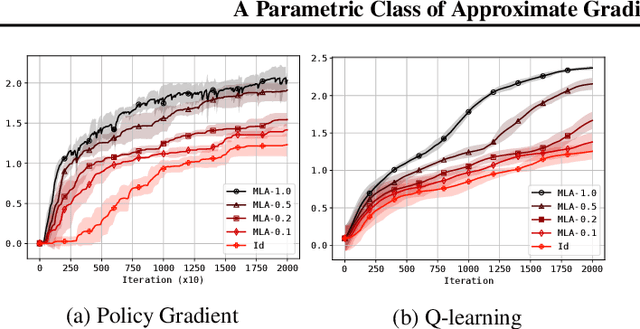
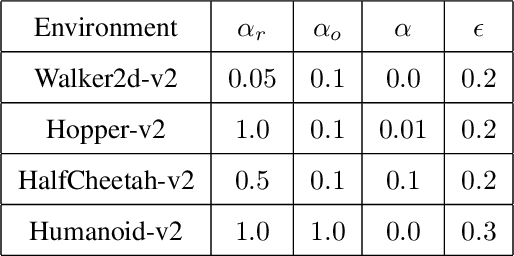
Approaches to policy optimization have been motivated from diverse principles, based on how the parametric model is interpreted (e.g. value versus policy representation) or how the learning objective is formulated, yet they share a common goal of maximizing expected return. To better capture the commonalities and identify key differences between policy optimization methods, we develop a unified perspective that re-expresses the underlying updates in terms of a limited choice of gradient form and scaling function. In particular, we identify a parameterized space of approximate gradient updates for policy optimization that is highly structured, yet covers both classical and recent examples, including PPO. As a result, we obtain novel yet well motivated updates that generalize existing algorithms in a way that can deliver benefits both in terms of convergence speed and final result quality. An experimental investigation demonstrates that the additional degrees of freedom provided in the parameterized family of updates can be leveraged to obtain non-trivial improvements both in synthetic domains and on popular deep RL benchmarks.

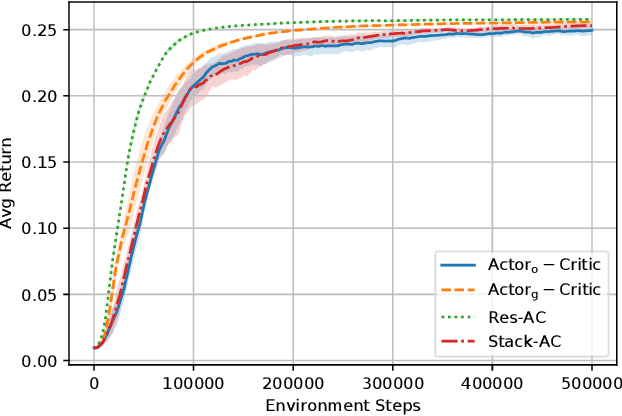
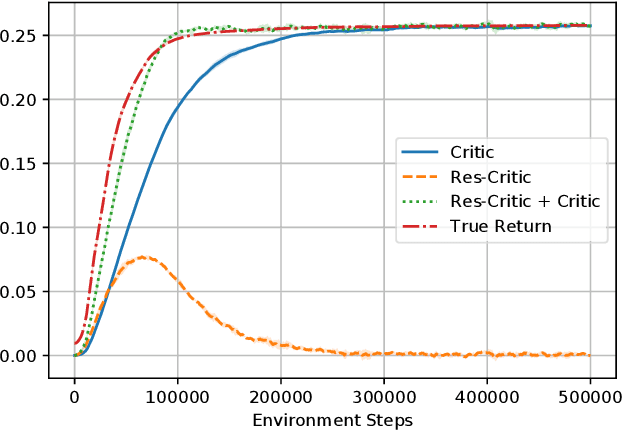
Characterizing the Gap Between Actor-Critic and Policy Gradient

Actor-critic (AC) methods are ubiquitous in reinforcement learning. Although it is understood that AC methods are closely related to policy gradient (PG), their precise connection has not been fully characterized previously. In this paper, we explain the gap between AC and PG methods by identifying the exact adjustment to the AC objective/gradient that recovers the true policy gradient of the cumulative reward objective (PG). Furthermore, by viewing the AC method as a two-player Stackelberg game between the actor and critic, we show that the Stackelberg policy gradient can be recovered as a special case of our more general analysis. Based on these results, we develop practical algorithms, Residual Actor-Critic and Stackelberg Actor-Critic, for estimating the correction between AC and PG and use these to modify the standard AC algorithm. Experiments on popular tabular and continuous environments show the proposed corrections can improve both the sample efficiency and final performance of existing AC methods.

Variational Rejection Sampling

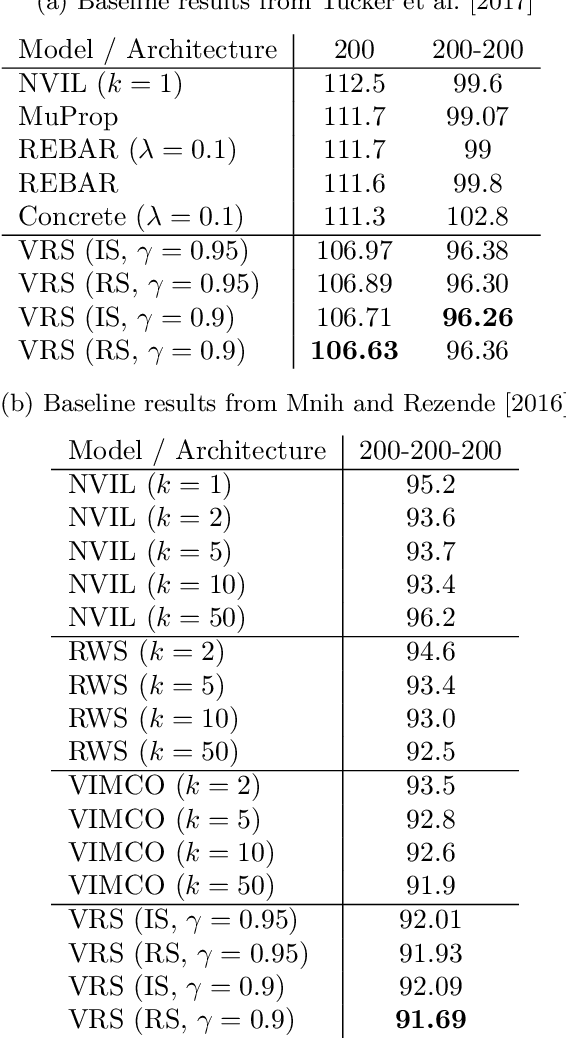
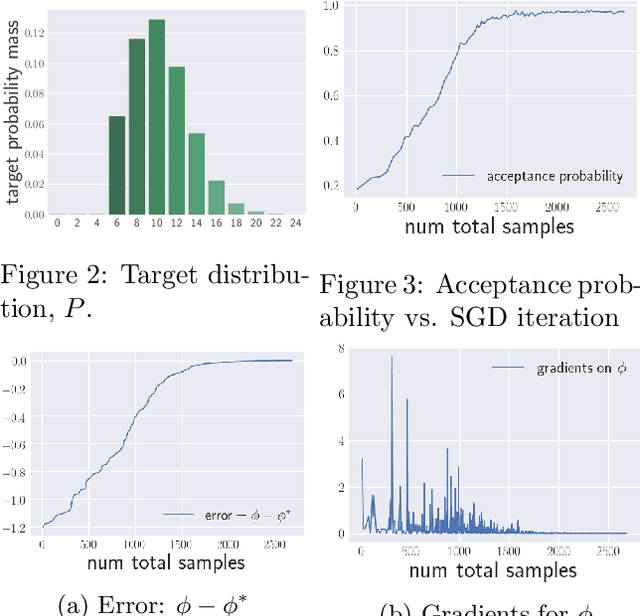
Learning latent variable models with stochastic variational inference is challenging when the approximate posterior is far from the true posterior, due to high variance in the gradient estimates. We propose a novel rejection sampling step that discards samples from the variational posterior which are assigned low likelihoods by the model. Our approach provides an arbitrarily accurate approximation of the true posterior at the expense of extra computation. Using a new gradient estimator for the resulting unnormalized proposal distribution, we achieve average improvements of 3.71 nats and 0.21 nats over state-of-the-art single-sample and multi-sample alternatives respectively for estimating marginal log-likelihoods using sigmoid belief networks on the MNIST dataset.