A Parametric Class of Approximate Gradient Updates for Policy Optimization
Paper and Code
Jun 17, 2022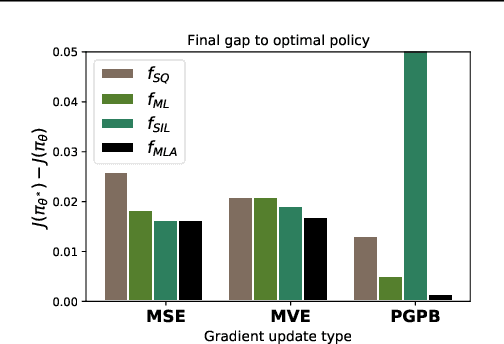

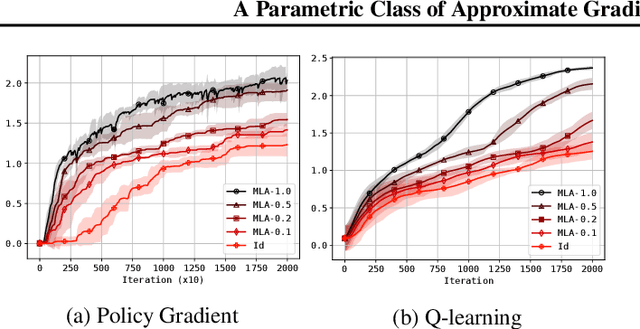
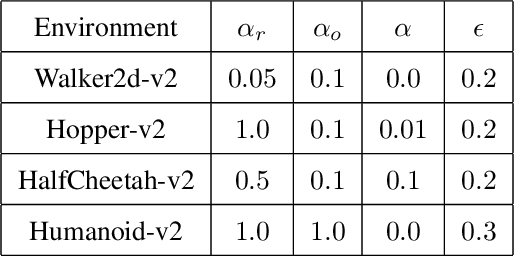
Approaches to policy optimization have been motivated from diverse principles, based on how the parametric model is interpreted (e.g. value versus policy representation) or how the learning objective is formulated, yet they share a common goal of maximizing expected return. To better capture the commonalities and identify key differences between policy optimization methods, we develop a unified perspective that re-expresses the underlying updates in terms of a limited choice of gradient form and scaling function. In particular, we identify a parameterized space of approximate gradient updates for policy optimization that is highly structured, yet covers both classical and recent examples, including PPO. As a result, we obtain novel yet well motivated updates that generalize existing algorithms in a way that can deliver benefits both in terms of convergence speed and final result quality. An experimental investigation demonstrates that the additional degrees of freedom provided in the parameterized family of updates can be leveraged to obtain non-trivial improvements both in synthetic domains and on popular deep RL benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge