Efficient Exploration for LLMs

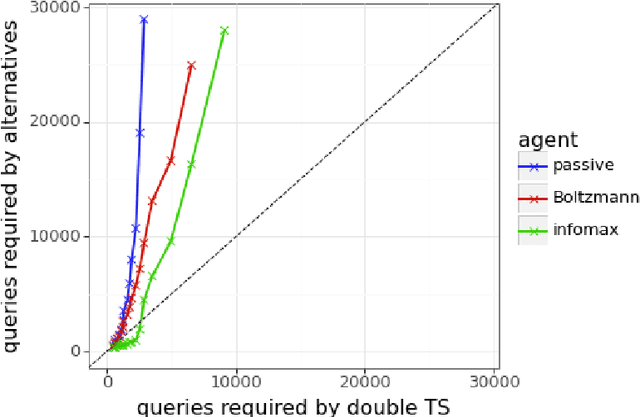
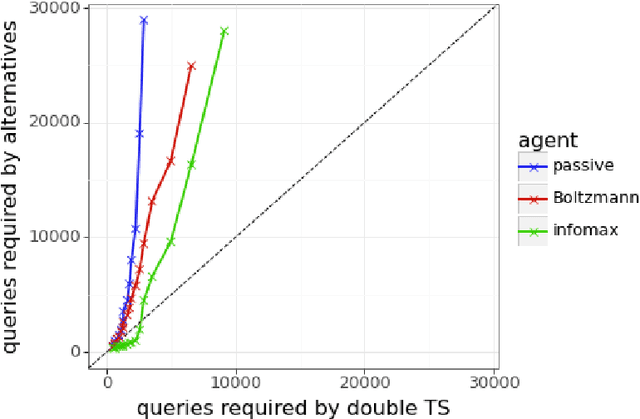
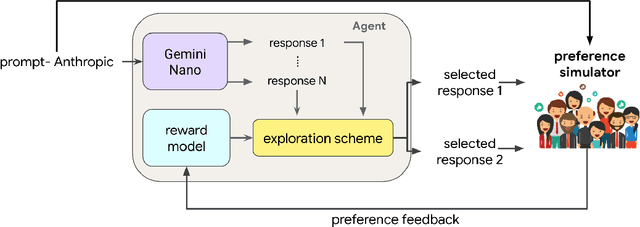
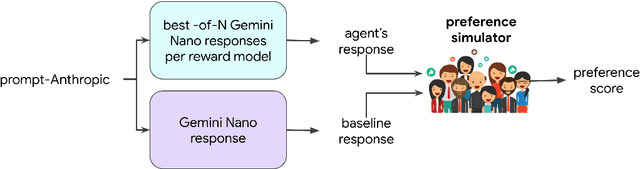
We present evidence of substantial benefit from efficient exploration in gathering human feedback to improve large language models. In our experiments, an agent sequentially generates queries while fitting a reward model to the feedback received. Our best-performing agent generates queries using double Thompson sampling, with uncertainty represented by an epistemic neural network. Our results demonstrate that efficient exploration enables high levels of performance with far fewer queries. Further, both uncertainty estimation and the choice of exploration scheme play critical roles.

Approximate Thompson Sampling via Epistemic Neural Networks

Thompson sampling (TS) is a popular heuristic for action selection, but it requires sampling from a posterior distribution. Unfortunately, this can become computationally intractable in complex environments, such as those modeled using neural networks. Approximate posterior samples can produce effective actions, but only if they reasonably approximate joint predictive distributions of outputs across inputs. Notably, accuracy of marginal predictive distributions does not suffice. Epistemic neural networks (ENNs) are designed to produce accurate joint predictive distributions. We compare a range of ENNs through computational experiments that assess their performance in approximating TS across bandit and reinforcement learning environments. The results indicate that ENNs serve this purpose well and illustrate how the quality of joint predictive distributions drives performance. Further, we demonstrate that the \textit{epinet} -- a small additive network that estimates uncertainty -- matches the performance of large ensembles at orders of magnitude lower computational cost. This enables effective application of TS with computation that scales gracefully to complex environments.

Robustness of Epinets against Distributional Shifts

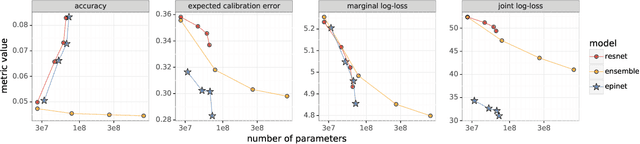
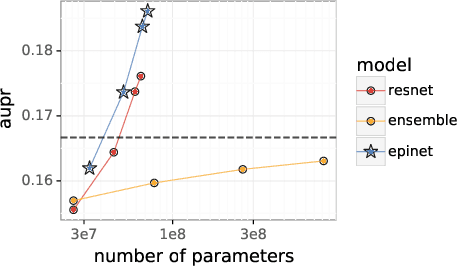
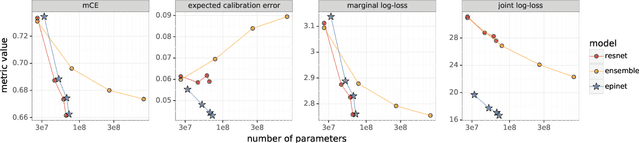
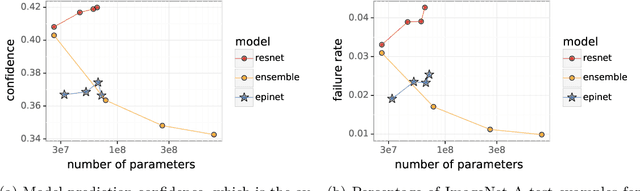
Recent work introduced the epinet as a new approach to uncertainty modeling in deep learning. An epinet is a small neural network added to traditional neural networks, which, together, can produce predictive distributions. In particular, using an epinet can greatly improve the quality of joint predictions across multiple inputs, a measure of how well a neural network knows what it does not know. In this paper, we examine whether epinets can offer similar advantages under distributional shifts. We find that, across ImageNet-A/O/C, epinets generally improve robustness metrics. Moreover, these improvements are more significant than those afforded by even very large ensembles at orders of magnitude lower computational costs. However, these improvements are relatively small compared to the outstanding issues in distributionally-robust deep learning. Epinets may be a useful tool in the toolbox, but they are far from the complete solution.

Ensembles for Uncertainty Estimation: Benefits of Prior Functions and Bootstrapping

In machine learning, an agent needs to estimate uncertainty to efficiently explore and adapt and to make effective decisions. A common approach to uncertainty estimation maintains an ensemble of models. In recent years, several approaches have been proposed for training ensembles, and conflicting views prevail with regards to the importance of various ingredients of these approaches. In this paper, we aim to address the benefits of two ingredients -- prior functions and bootstrapping -- which have come into question. We show that prior functions can significantly improve an ensemble agent's joint predictions across inputs and that bootstrapping affords additional benefits if the signal-to-noise ratio varies across inputs. Our claims are justified by both theoretical and experimental results.

Evaluating High-Order Predictive Distributions in Deep Learning

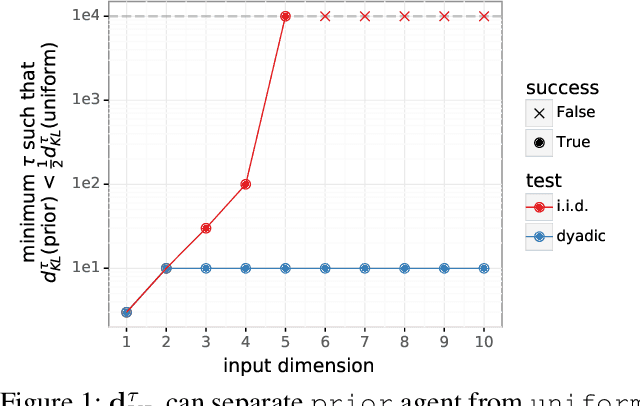
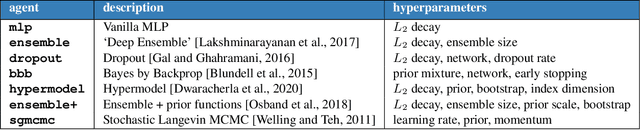
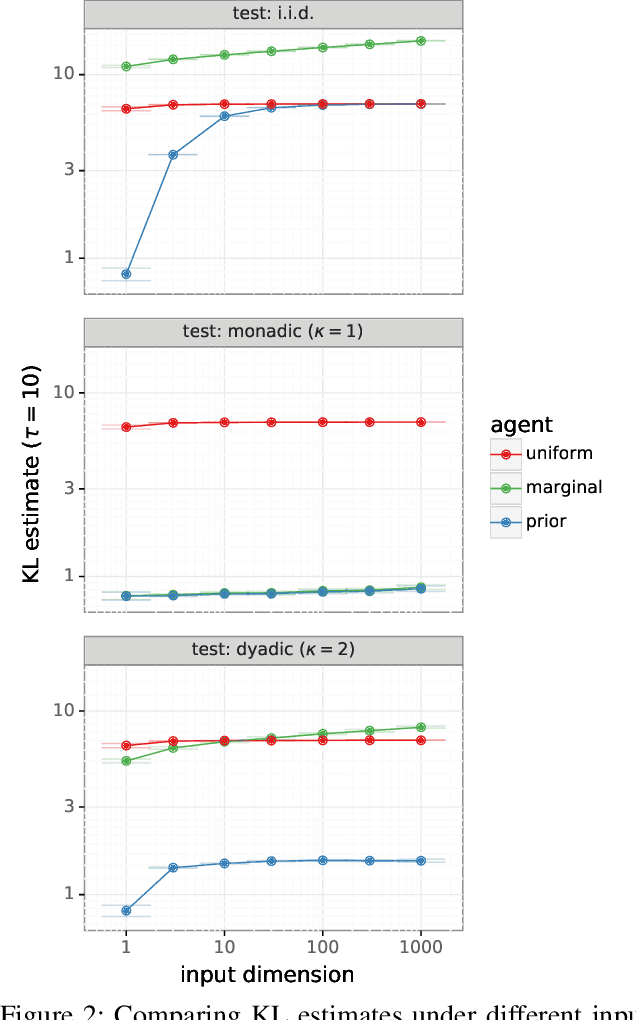
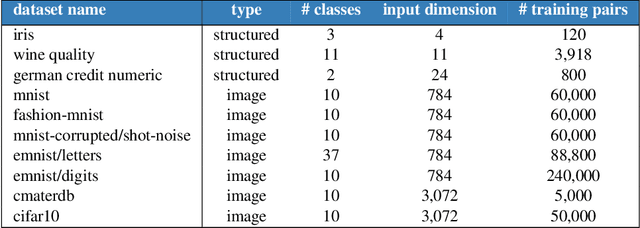
Most work on supervised learning research has focused on marginal predictions. In decision problems, joint predictive distributions are essential for good performance. Previous work has developed methods for assessing low-order predictive distributions with inputs sampled i.i.d. from the testing distribution. With low-dimensional inputs, these methods distinguish agents that effectively estimate uncertainty from those that do not. We establish that the predictive distribution order required for such differentiation increases greatly with input dimension, rendering these methods impractical. To accommodate high-dimensional inputs, we introduce \textit{dyadic sampling}, which focuses on predictive distributions associated with random \textit{pairs} of inputs. We demonstrate that this approach efficiently distinguishes agents in high-dimensional examples involving simple logistic regression as well as complex synthetic and empirical data.

Evaluating Predictive Distributions: Does Bayesian Deep Learning Work?

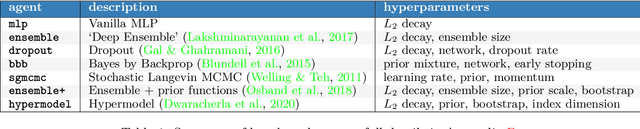
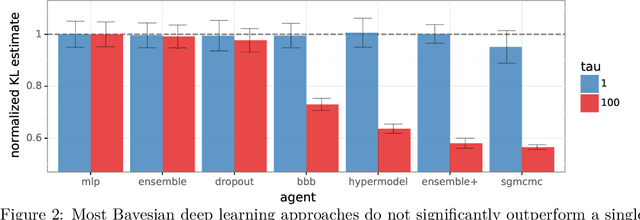
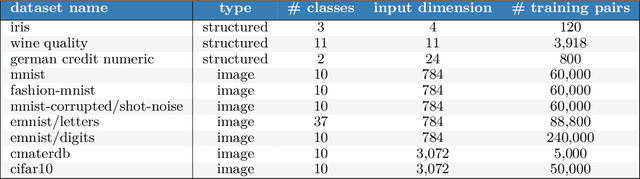
Posterior predictive distributions quantify uncertainties ignored by point estimates. This paper introduces \textit{The Neural Testbed}, which provides tools for the systematic evaluation of agents that generate such predictions. Crucially, these tools assess not only the quality of marginal predictions per input, but also joint predictions given many inputs. Joint distributions are often critical for useful uncertainty quantification, but they have been largely overlooked by the Bayesian deep learning community. We benchmark several approaches to uncertainty estimation using a neural-network-based data generating process. Our results reveal the importance of evaluation beyond marginal predictions. Further, they reconcile sources of confusion in the field, such as why Bayesian deep learning approaches that generate accurate marginal predictions perform poorly in sequential decision tasks, how incorporating priors can be helpful, and what roles epistemic versus aleatoric uncertainty play when evaluating performance. We also present experiments on real-world challenge datasets, which show a high correlation with testbed results, and that the importance of evaluating joint predictive distributions carries over to real data. As part of this effort, we opensource The Neural Testbed, including all implementations from this paper.

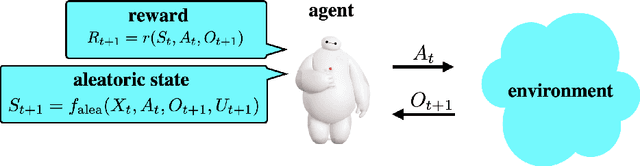
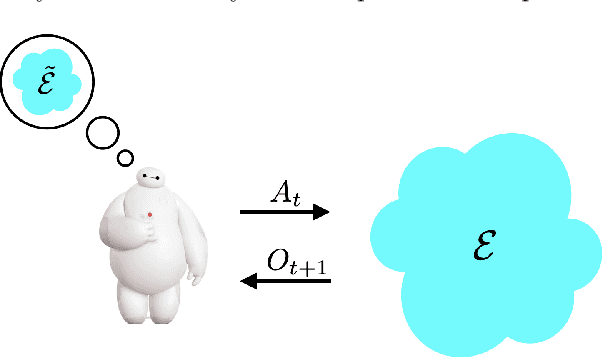
Reinforcement Learning, Bit by Bit

Reinforcement learning agents have demonstrated remarkable achievements in simulated environments. Data efficiency poses an impediment to carrying this success over to real environments. The design of data-efficient agents calls for a deeper understanding of information acquisition and representation. We develop concepts and establish a regret bound that together offer principled guidance. The bound sheds light on questions of what information to seek, how to seek that information, and it what information to retain. To illustrate concepts, we design simple agents that build on them and present computational results that demonstrate improvements in data efficiency.

Hypermodels for Exploration

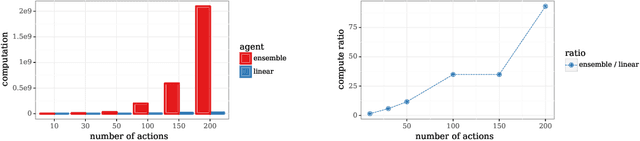
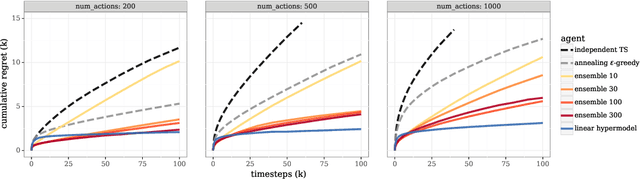
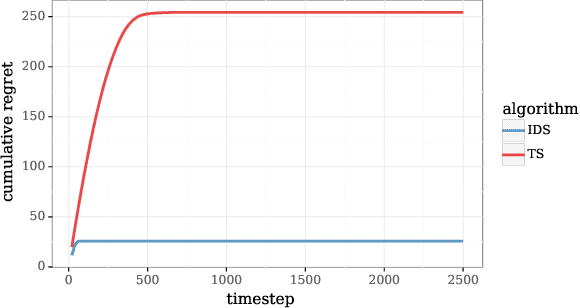
We study the use of hypermodels to represent epistemic uncertainty and guide exploration. This generalizes and extends the use of ensembles to approximate Thompson sampling. The computational cost of training an ensemble grows with its size, and as such, prior work has typically been limited to ensembles with tens of elements. We show that alternative hypermodels can enjoy dramatic efficiency gains, enabling behavior that would otherwise require hundreds or thousands of elements, and even succeed in situations where ensemble methods fail to learn regardless of size. This allows more accurate approximation of Thompson sampling as well as use of more sophisticated exploration schemes. In particular, we consider an approximate form of information-directed sampling and demonstrate performance gains relative to Thompson sampling. As alternatives to ensembles, we consider linear and neural network hypermodels, also known as hypernetworks. We prove that, with neural network base models, a linear hypermodel can represent essentially any distribution over functions, and as such, hypernetworks are no more expressive.

Langevin DQN

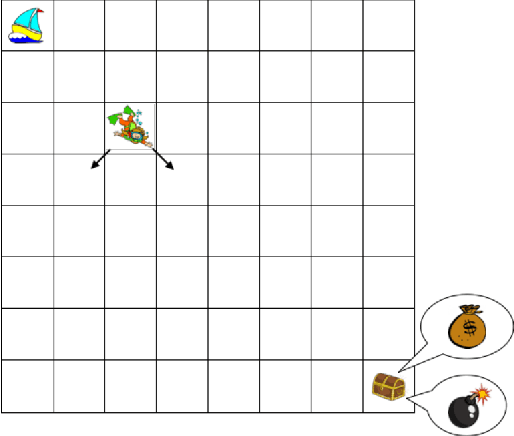
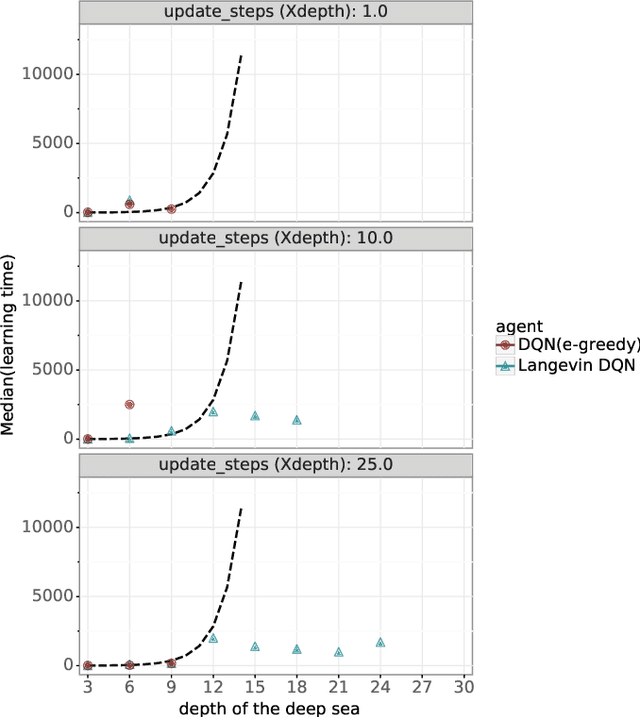
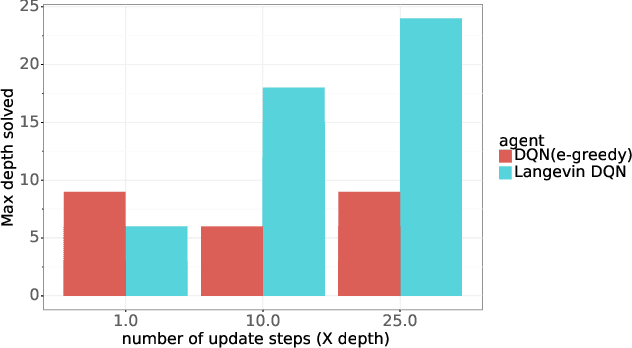
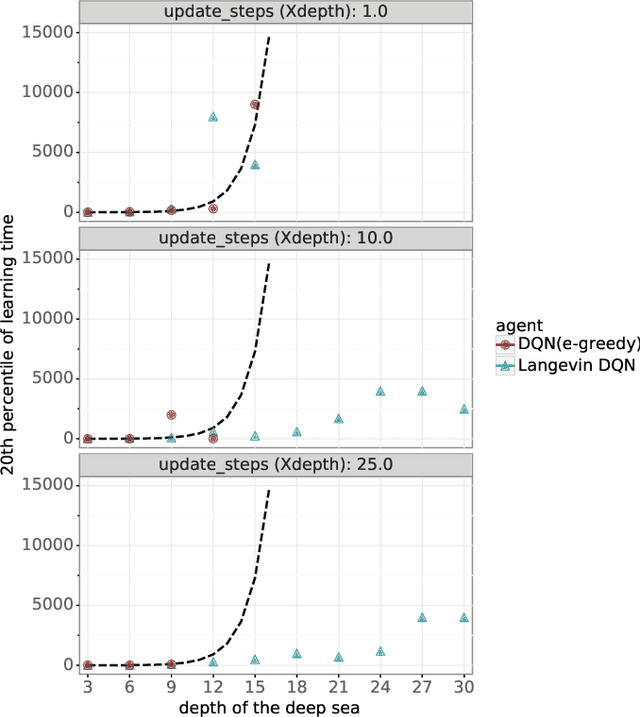
Algorithms that tackle deep exploration -- an important challenge in reinforcement learning -- have relied on epistemic uncertainty representation through ensembles or other hypermodels, exploration bonuses, or visitation count distributions. An open question is whether deep exploration can be achieved by an incremental reinforcement learning algorithm that tracks a single point estimate, without additional complexity required to account for epistemic uncertainty. We answer this question in the affirmative. In particular, we develop Langevin DQN, a variation of DQN that differs only in perturbing parameter updates with Gaussian noise, and demonstrate through a computational study that the algorithm achieves deep exploration. We also provide an intuition for why Langevin DQN performs deep exploration.

Motion-based Object Segmentation based on Dense RGB-D Scene Flow

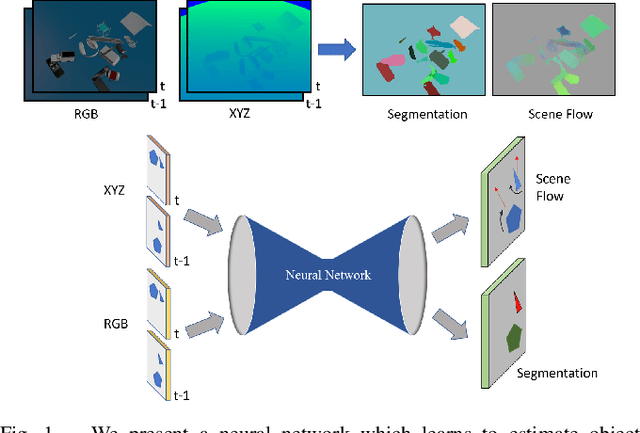
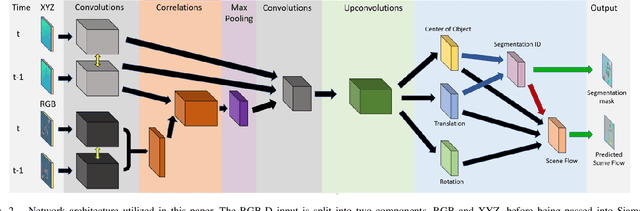
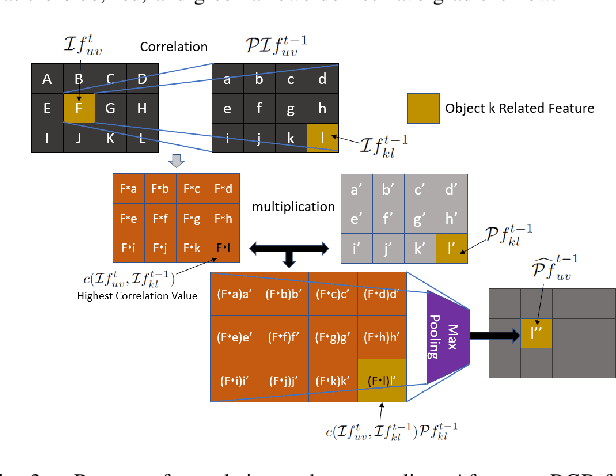
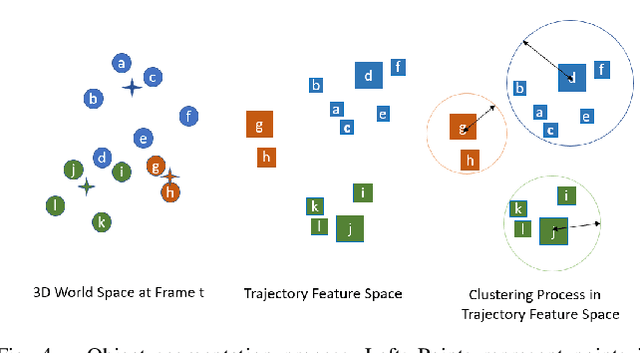
Given two consecutive RGB-D images, we propose a model that estimates a dense 3D motion field, also known as scene flow. We take advantage of the fact that in robot manipulation scenarios, scenes often consist of a set of rigidly moving objects. Our model jointly estimates (i) the segmentation of the scene into an unknown but finite number of objects, (ii) the motion trajectories of these objects and (iii) the object scene flow. We employ an hourglass, deep neural network architecture. In the encoding stage, the RGB and depth images undergo spatial compression and correlation. In the decoding stage, the model outputs three images containing a per-pixel estimate of the corresponding object center as well as object translation and rotation. This forms the basis for inferring the object segmentation and final object scene flow. To evaluate our model, we generated a new and challenging, large-scale, synthetic dataset that is specifically targeted at robotic manipulation: It contains a large number of scenes with a very diverse set of simultaneously moving 3D objects and is recorded with a simulated, static RGB-D camera. In quantitative experiments, we show that we outperform state-of-the-art scene flow and motion-segmentation methods on this data set. In qualitative experiments, we show how our learned model transfers to challenging real-world scenes, visually generating better results than existing methods.