Multi-Objective Preference Optimization: Improving Human Alignment of Generative Models

Post-training of LLMs with RLHF, and subsequently preference optimization algorithms such as DPO, IPO, etc., made a big difference in improving human alignment. However, all such techniques can only work with a single (human) objective. In practice, human users have multiple objectives, such as helpfulness and harmlessness, and there is no natural way to aggregate them into a single objective. In this paper, we address the multi-objective preference-alignment problem, where a policy must optimize several, potentially conflicting, objectives. We introduce the Multi-Objective Preference Optimization (MOPO) algorithm, which frames alignment as a constrained KL-regularized optimization: the primary objective is maximized while secondary objectives are lower-bounded by tunable safety thresholds. Unlike prior work, MOPO operates directly on pairwise preference data, requires no point-wise reward assumption, and avoids heuristic prompt-context engineering. The method recovers policies on the Pareto front whenever the front is attainable; practically, it reduces to simple closed-form iterative updates suitable for large-scale training. On synthetic benchmarks with diverse canonical preference structures, we show that MOPO approximates the Pareto front. When fine-tuning a 1.3B-parameter language model on real-world human-preference datasets, MOPO attains higher rewards and yields policies that Pareto-dominate baselines; ablation studies confirm optimization stability and robustness to hyperparameters.

Best Policy Learning from Trajectory Preference Feedback

We address the problem of best policy identification in preference-based reinforcement learning (PbRL), where learning occurs from noisy binary preferences over trajectory pairs rather than explicit numerical rewards. This approach is useful for post-training optimization of generative AI models during multi-turn user interactions, where preference feedback is more robust than handcrafted reward models. In this setting, learning is driven by both an offline preference dataset -- collected from a rater of unknown 'competence' -- and online data collected with pure exploration. Since offline datasets may exhibit out-of-distribution (OOD) biases, principled online data collection is necessary. To address this, we propose Posterior Sampling for Preference Learning ($\mathsf{PSPL}$), a novel algorithm inspired by Top-Two Thompson Sampling, that maintains independent posteriors over the true reward model and transition dynamics. We provide the first theoretical guarantees for PbRL in this setting, establishing an upper bound on the simple Bayesian regret of $\mathsf{PSPL}$. Since the exact algorithm can be computationally impractical, we also provide an approximate version that outperforms existing baselines.

Evaluating Large Language Models on Financial Report Summarization: An Empirical Study

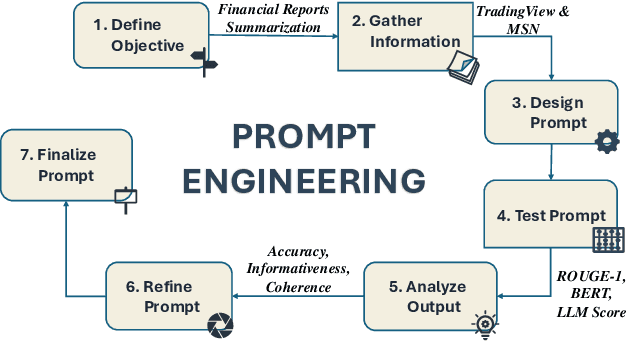
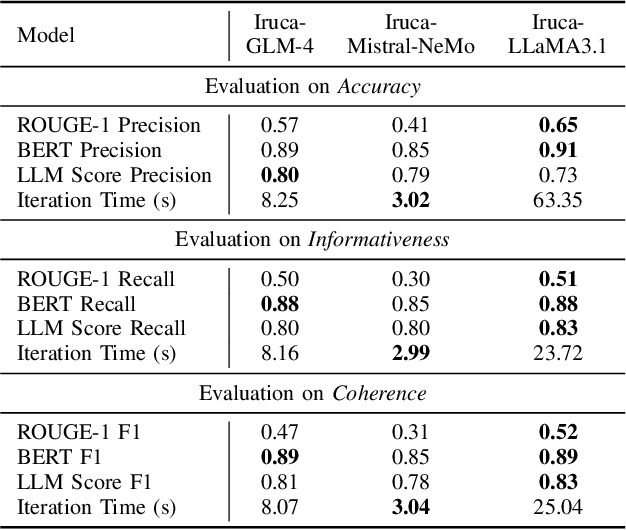
In recent years, Large Language Models (LLMs) have demonstrated remarkable versatility across various applications, including natural language understanding, domain-specific knowledge tasks, etc. However, applying LLMs to complex, high-stakes domains like finance requires rigorous evaluation to ensure reliability, accuracy, and compliance with industry standards. To address this need, we conduct a comprehensive and comparative study on three state-of-the-art LLMs, GLM-4, Mistral-NeMo, and LLaMA3.1, focusing on their effectiveness in generating automated financial reports. Our primary motivation is to explore how these models can be harnessed within finance, a field demanding precision, contextual relevance, and robustness against erroneous or misleading information. By examining each model's capabilities, we aim to provide an insightful assessment of their strengths and limitations. Our paper offers benchmarks for financial report analysis, encompassing proposed metrics such as ROUGE-1, BERT Score, and LLM Score. We introduce an innovative evaluation framework that integrates both quantitative metrics (e.g., precision, recall) and qualitative analyses (e.g., contextual fit, consistency) to provide a holistic view of each model's output quality. Additionally, we make our financial dataset publicly available, inviting researchers and practitioners to leverage, scrutinize, and enhance our findings through broader community engagement and collaborative improvement. Our dataset is available on huggingface.

Online Bandit Learning with Offline Preference Data

Reinforcement Learning with Human Feedback (RLHF) is at the core of fine-tuning methods for generative AI models for language and images. Such feedback is often sought as rank or preference feedback from human raters, as opposed to eliciting scores since the latter tends to be very noisy. On the other hand, RL theory and algorithms predominantly assume that a reward feedback is available. In particular, approaches for online learning that can be helpful in adaptive data collection via active learning cannot incorporate offline preference data. In this paper, we adopt a finite-armed linear bandit model as a prototypical model of online learning. We consider an offline preference dataset to be available generated by an expert of unknown 'competence'. We propose $\texttt{warmPref-PS}$, a posterior sampling algorithm for online learning that can be warm-started with an offline dataset with noisy preference feedback. We show that by modeling the competence of the expert that generated it, we are able to use such a dataset most effectively. We support our claims with novel theoretical analysis of its Bayesian regret, as well as extensive empirical evaluation of an approximate algorithm which performs substantially better (almost 25 to 50% regret reduction in our studies) as compared to baselines.

RLHF and IIA: Perverse Incentives

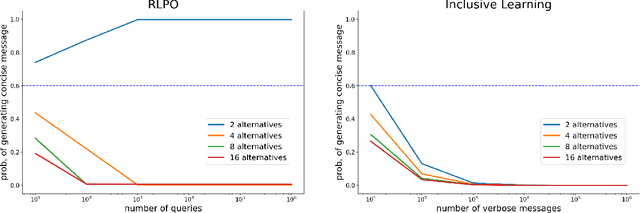
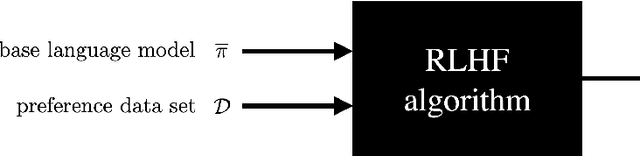
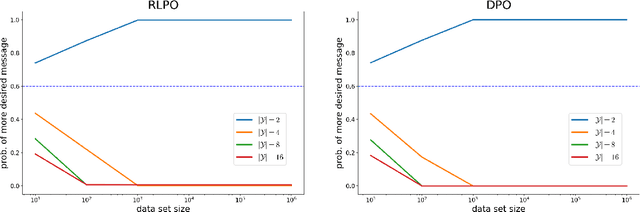
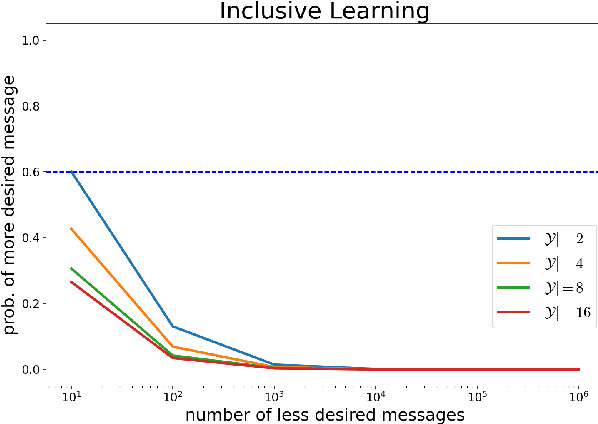
Existing algorithms for reinforcement learning from human feedback (RLHF) can incentivize responses at odds with preferences because they are based on models that assume independence of irrelevant alternatives (IIA). The perverse incentives induced by IIA give rise to egregious behavior when innovating on query formats or learning algorithms.

Efficient Online Learning with Offline Datasets for Infinite Horizon MDPs: A Bayesian Approach

In this paper, we study the problem of efficient online reinforcement learning in the infinite horizon setting when there is an offline dataset to start with. We assume that the offline dataset is generated by an expert but with unknown level of competence, i.e., it is not perfect and not necessarily using the optimal policy. We show that if the learning agent models the behavioral policy (parameterized by a competence parameter) used by the expert, it can do substantially better in terms of minimizing cumulative regret, than if it doesn't do that. We establish an upper bound on regret of the exact informed PSRL algorithm that scales as $\tilde{O}(\sqrt{T})$. This requires a novel prior-dependent regret analysis of Bayesian online learning algorithms for the infinite horizon setting. We then propose an approximate Informed RLSVI algorithm that we can interpret as performing imitation learning with the offline dataset, and then performing online learning.

Bridging Imitation and Online Reinforcement Learning: An Optimistic Tale

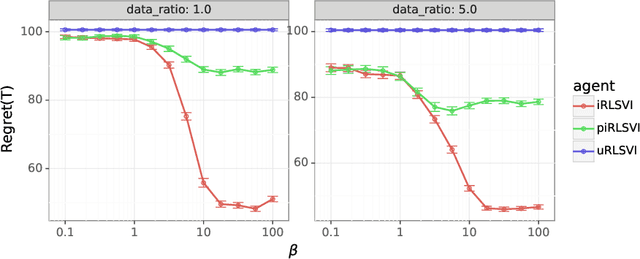
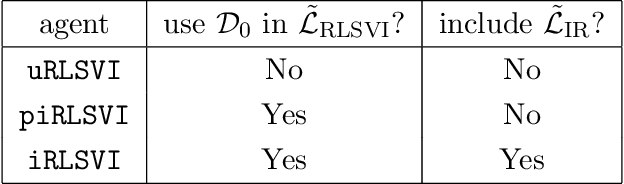
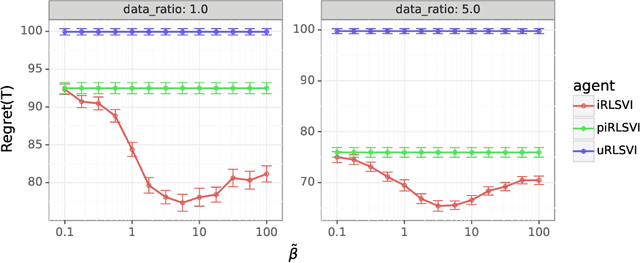
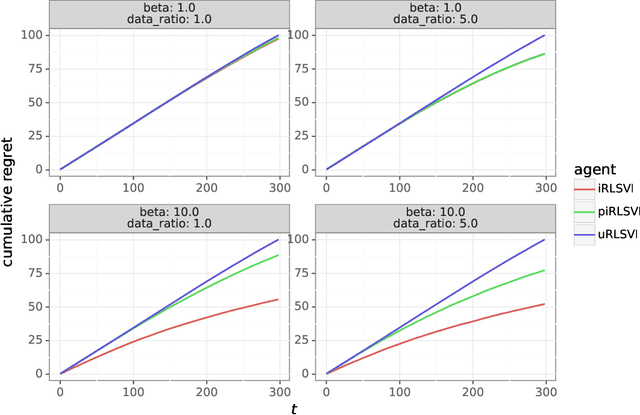
In this paper, we address the following problem: Given an offline demonstration dataset from an imperfect expert, what is the best way to leverage it to bootstrap online learning performance in MDPs. We first propose an Informed Posterior Sampling-based RL (iPSRL) algorithm that uses the offline dataset, and information about the expert's behavioral policy used to generate the offline dataset. Its cumulative Bayesian regret goes down to zero exponentially fast in N, the offline dataset size if the expert is competent enough. Since this algorithm is computationally impractical, we then propose the iRLSVI algorithm that can be seen as a combination of the RLSVI algorithm for online RL, and imitation learning. Our empirical results show that the proposed iRLSVI algorithm is able to achieve significant reduction in regret as compared to two baselines: no offline data, and offline dataset but used without information about the generative policy. Our algorithm bridges online RL and imitation learning for the first time.

Approximate Thompson Sampling via Epistemic Neural Networks

Thompson sampling (TS) is a popular heuristic for action selection, but it requires sampling from a posterior distribution. Unfortunately, this can become computationally intractable in complex environments, such as those modeled using neural networks. Approximate posterior samples can produce effective actions, but only if they reasonably approximate joint predictive distributions of outputs across inputs. Notably, accuracy of marginal predictive distributions does not suffice. Epistemic neural networks (ENNs) are designed to produce accurate joint predictive distributions. We compare a range of ENNs through computational experiments that assess their performance in approximating TS across bandit and reinforcement learning environments. The results indicate that ENNs serve this purpose well and illustrate how the quality of joint predictive distributions drives performance. Further, we demonstrate that the \textit{epinet} -- a small additive network that estimates uncertainty -- matches the performance of large ensembles at orders of magnitude lower computational cost. This enables effective application of TS with computation that scales gracefully to complex environments.

Leveraging Demonstrations to Improve Online Learning: Quality Matters

We investigate the extent to which offline demonstration data can improve online learning. It is natural to expect some improvement, but the question is how, and by how much? We show that the degree of improvement must depend on the quality of the demonstration data. To generate portable insights, we focus on Thompson sampling (TS) applied to a multi-armed bandit as a prototypical online learning algorithm and model. The demonstration data is generated by an expert with a given competence level, a notion we introduce. We propose an informed TS algorithm that utilizes the demonstration data in a coherent way through Bayes' rule and derive a prior-dependent Bayesian regret bound. This offers insight into how pretraining can greatly improve online performance and how the degree of improvement increases with the expert's competence level. We also develop a practical, approximate informed TS algorithm through Bayesian bootstrapping and show substantial empirical regret reduction through experiments.

Robustness of Epinets against Distributional Shifts

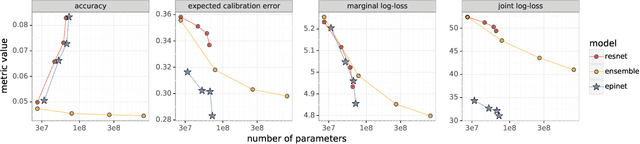
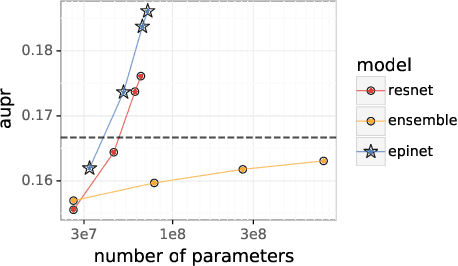
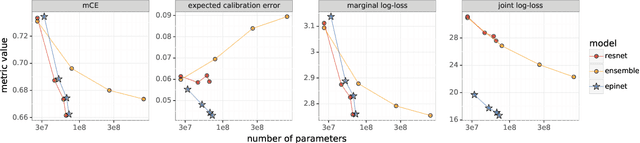
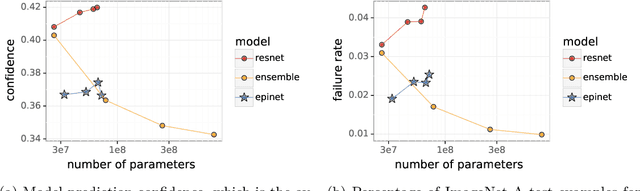
Recent work introduced the epinet as a new approach to uncertainty modeling in deep learning. An epinet is a small neural network added to traditional neural networks, which, together, can produce predictive distributions. In particular, using an epinet can greatly improve the quality of joint predictions across multiple inputs, a measure of how well a neural network knows what it does not know. In this paper, we examine whether epinets can offer similar advantages under distributional shifts. We find that, across ImageNet-A/O/C, epinets generally improve robustness metrics. Moreover, these improvements are more significant than those afforded by even very large ensembles at orders of magnitude lower computational costs. However, these improvements are relatively small compared to the outstanding issues in distributionally-robust deep learning. Epinets may be a useful tool in the toolbox, but they are far from the complete solution.