Evaluating High-Order Predictive Distributions in Deep Learning
Paper and Code
Feb 28, 2022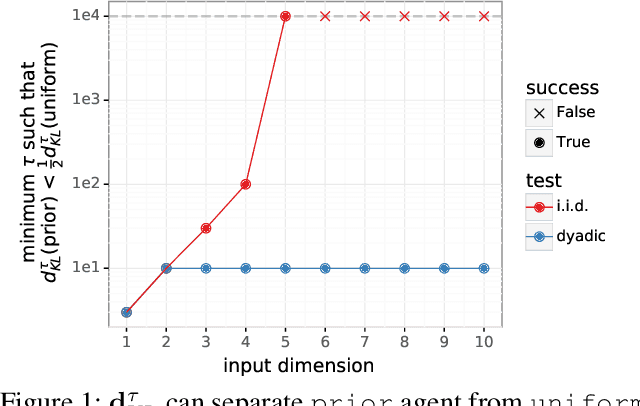
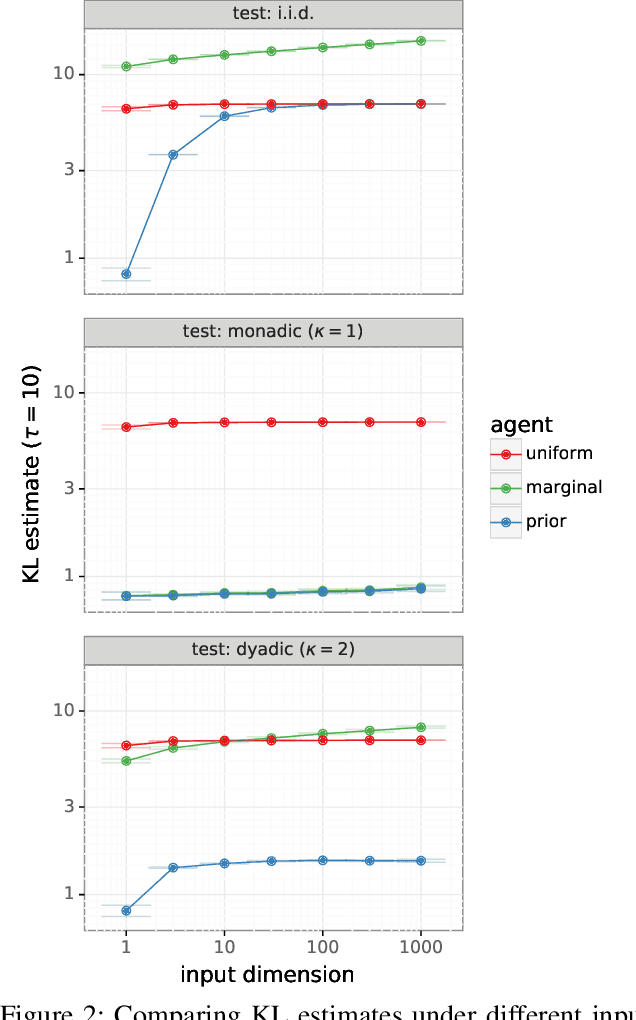
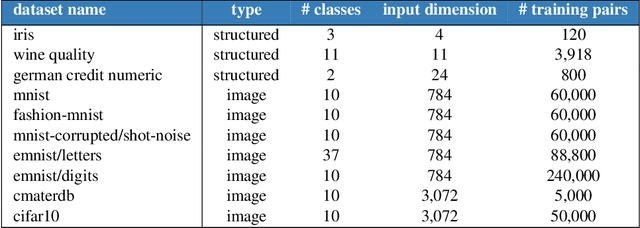
Most work on supervised learning research has focused on marginal predictions. In decision problems, joint predictive distributions are essential for good performance. Previous work has developed methods for assessing low-order predictive distributions with inputs sampled i.i.d. from the testing distribution. With low-dimensional inputs, these methods distinguish agents that effectively estimate uncertainty from those that do not. We establish that the predictive distribution order required for such differentiation increases greatly with input dimension, rendering these methods impractical. To accommodate high-dimensional inputs, we introduce \textit{dyadic sampling}, which focuses on predictive distributions associated with random \textit{pairs} of inputs. We demonstrate that this approach efficiently distinguishes agents in high-dimensional examples involving simple logistic regression as well as complex synthetic and empirical data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge