Hypermodels for Exploration
Paper and Code
Jun 12, 2020
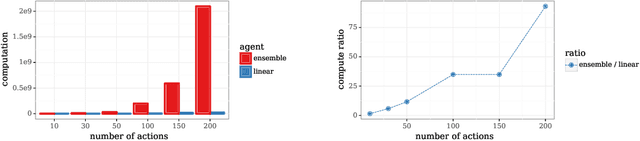
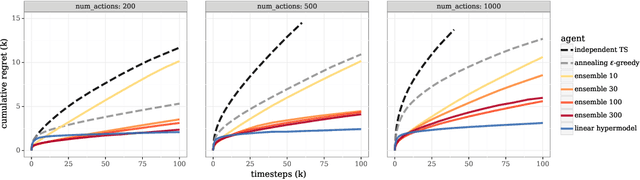
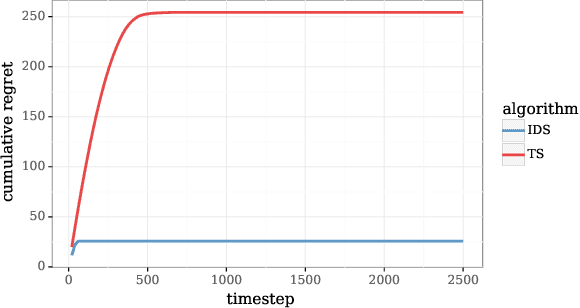
We study the use of hypermodels to represent epistemic uncertainty and guide exploration. This generalizes and extends the use of ensembles to approximate Thompson sampling. The computational cost of training an ensemble grows with its size, and as such, prior work has typically been limited to ensembles with tens of elements. We show that alternative hypermodels can enjoy dramatic efficiency gains, enabling behavior that would otherwise require hundreds or thousands of elements, and even succeed in situations where ensemble methods fail to learn regardless of size. This allows more accurate approximation of Thompson sampling as well as use of more sophisticated exploration schemes. In particular, we consider an approximate form of information-directed sampling and demonstrate performance gains relative to Thompson sampling. As alternatives to ensembles, we consider linear and neural network hypermodels, also known as hypernetworks. We prove that, with neural network base models, a linear hypermodel can represent essentially any distribution over functions, and as such, hypernetworks are no more expressive.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge