Universal computation is intrinsic to language model decoding

Language models now provide an interface to express and often solve general problems in natural language, yet their ultimate computational capabilities remain a major topic of scientific debate. Unlike a formal computer, a language model is trained to autoregressively predict successive elements in human-generated text. We prove that chaining a language model's autoregressive output is sufficient to perform universal computation. That is, a language model can simulate the execution of any algorithm on any input. The challenge of eliciting desired computational behaviour can thus be reframed in terms of programmability: the ease of finding a suitable prompt. Strikingly, we demonstrate that even randomly initialized language models are capable of universal computation before training. This implies that training does not give rise to computational expressiveness -- rather, it improves programmability, enabling a natural language interface for accessing these intrinsic capabilities.

The World Is Bigger! A Computationally-Embedded Perspective on the Big World Hypothesis

Continual learning is often motivated by the idea, known as the big world hypothesis, that "the world is bigger" than the agent. Recent problem formulations capture this idea by explicitly constraining an agent relative to the environment. These constraints lead to solutions in which the agent continually adapts to best use its limited capacity, rather than converging to a fixed solution. However, explicit constraints can be ad hoc, difficult to incorporate, and may limit the effectiveness of scaling up the agent's capacity. In this paper, we characterize a problem setting in which an agent, regardless of its capacity, is constrained by being embedded in the environment. In particular, we introduce a computationally-embedded perspective that represents an embedded agent as an automaton simulated within a universal (formal) computer. Such an automaton is always constrained; we prove that it is equivalent to an agent that interacts with a partially observable Markov decision process over a countably infinite state-space. We propose an objective for this setting, which we call interactivity, that measures an agent's ability to continually adapt its behaviour by learning new predictions. We then develop a model-based reinforcement learning algorithm for interactivity-seeking, and use it to construct a synthetic problem to evaluate continual learning capability. Our results show that deep nonlinear networks struggle to sustain interactivity, whereas deep linear networks sustain higher interactivity as capacity increases.

Plastic Learning with Deep Fourier Features

Deep neural networks can struggle to learn continually in the face of non-stationarity. This phenomenon is known as loss of plasticity. In this paper, we identify underlying principles that lead to plastic algorithms. In particular, we provide theoretical results showing that linear function approximation, as well as a special case of deep linear networks, do not suffer from loss of plasticity. We then propose deep Fourier features, which are the concatenation of a sine and cosine in every layer, and we show that this combination provides a dynamic balance between the trainability obtained through linearity and the effectiveness obtained through the nonlinearity of neural networks. Deep networks composed entirely of deep Fourier features are highly trainable and sustain their trainability over the course of learning. Our empirical results show that continual learning performance can be drastically improved by replacing ReLU activations with deep Fourier features. These results hold for different continual learning scenarios (e.g., label noise, class incremental learning, pixel permutations) on all major supervised learning datasets used for continual learning research, such as CIFAR10, CIFAR100, and tiny-ImageNet.

The Need for a Big World Simulator: A Scientific Challenge for Continual Learning

The "small agent, big world" frame offers a conceptual view that motivates the need for continual learning. The idea is that a small agent operating in a much bigger world cannot store all information that the world has to offer. To perform well, the agent must be carefully designed to ingest, retain, and eject the right information. To enable the development of performant continual learning agents, a number of synthetic environments have been proposed. However, these benchmarks suffer from limitations, including unnatural distribution shifts and a lack of fidelity to the "small agent, big world" framing. This paper aims to formalize two desiderata for the design of future simulated environments. These two criteria aim to reflect the objectives and complexity of continual learning in practical settings while enabling rapid prototyping of algorithms on a smaller scale.

Learning Continually by Spectral Regularization

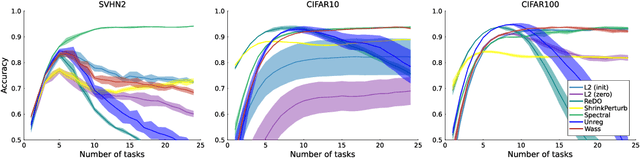
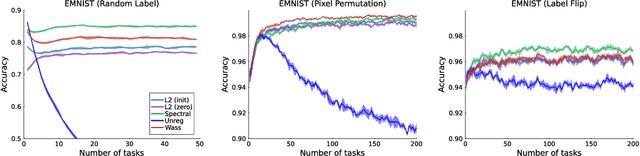
Loss of plasticity is a phenomenon where neural networks become more difficult to train during the course of learning. Continual learning algorithms seek to mitigate this effect by sustaining good predictive performance while maintaining network trainability. We develop new techniques for improving continual learning by first reconsidering how initialization can ensure trainability during early phases of learning. From this perspective, we derive new regularization strategies for continual learning that ensure beneficial initialization properties are better maintained throughout training. In particular, we investigate two new regularization techniques for continual learning: (i) Wasserstein regularization toward the initial weight distribution, which is less restrictive than regularizing toward initial weights; and (ii) regularizing weight matrix singular values, which directly ensures gradient diversity is maintained throughout training. We present an experimental analysis that shows these alternative regularizers can improve continual learning performance across a range of supervised learning tasks and model architectures. The alternative regularizers prove to be less sensitive to hyperparameters while demonstrating better training in individual tasks, sustaining trainability as new tasks arrive, and achieving better generalization performance.

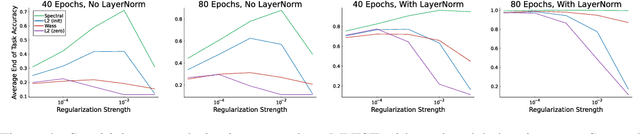
Curvature Explains Loss of Plasticity

Loss of plasticity is a phenomenon in which neural networks lose their ability to learn from new experience. Despite being empirically observed in several problem settings, little is understood about the mechanisms that lead to loss of plasticity. In this paper, we offer a consistent explanation for plasticity loss, based on an assertion that neural networks lose directions of curvature during training and that plasticity loss can be attributed to this reduction in curvature. To support such a claim, we provide a systematic empirical investigation of plasticity loss across several continual supervised learning problems. Our findings illustrate that curvature loss coincides with and sometimes precedes plasticity loss, while also showing that previous explanations are insufficient to explain loss of plasticity in all settings. Lastly, we show that regularizers which mitigate loss of plasticity also preserve curvature, motivating a simple distributional regularizer that proves to be effective across the problem settings considered.

Reinforcement Teaching

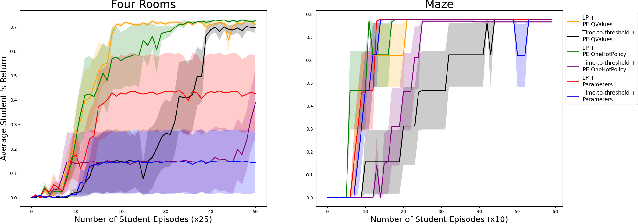
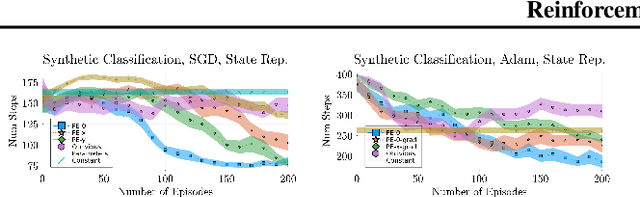
We propose Reinforcement Teaching: a framework for meta-learning in which a teaching policy is learned, through reinforcement, to control a student's learning process. The student's learning process is modelled as a Markov reward process and the teacher, with its action-space, interacts with the induced Markov decision process. We show that, for many learning processes, the student's learnable parameters form a Markov state. To avoid having the teacher learn directly from parameters, we propose the Parameter Embedder that learns a representation of a student's state from its input/output behaviour. Next, we use learning progress to shape the teacher's reward towards maximizing the student's performance. To demonstrate the generality of Reinforcement Teaching, we conducted experiments in which a teacher learns to significantly improve supervised and reinforcement learners by using a combination of learning progress reward and a Parameter Embedded state. These results show that Reinforcement Teaching is not only an expressive framework capable of unifying different approaches, but also provides meta-learning with the plethora of tools from reinforcement learning.

ZORB: A Derivative-Free Backpropagation Algorithm for Neural Networks

Gradient descent and backpropagation have enabled neural networks to achieve remarkable results in many real-world applications. Despite ongoing success, training a neural network with gradient descent can be a slow and strenuous affair. We present a simple yet faster training algorithm called Zeroth-Order Relaxed Backpropagation (ZORB). Instead of calculating gradients, ZORB uses the pseudoinverse of targets to backpropagate information. ZORB is designed to reduce the time required to train deep neural networks without penalizing performance. To illustrate the speed up, we trained a feed-forward neural network with 11 layers on MNIST and observed that ZORB converged 300 times faster than Adam while achieving a comparable error rate, without any hyperparameter tuning. We also broaden the scope of ZORB to convolutional neural networks, and apply it to subsamples of the CIFAR-10 dataset. Experiments on standard classification and regression benchmarks demonstrate ZORB's advantage over traditional backpropagation with Gradient Descent.