Aligning AI Agents via Information-Directed Sampling

The staggering feats of AI systems have brought to attention the topic of AI Alignment: aligning a "superintelligent" AI agent's actions with humanity's interests. Many existing frameworks/algorithms in alignment study the problem on a myopic horizon or study learning from human feedback in isolation, relying on the contrived assumption that the agent has already perfectly identified the environment. As a starting point to address these limitations, we define a class of bandit alignment problems as an extension of classic multi-armed bandit problems. A bandit alignment problem involves an agent tasked with maximizing long-run expected reward by interacting with an environment and a human, both involving details/preferences initially unknown to the agent. The reward of actions in the environment depends on both observed outcomes and human preferences. Furthermore, costs are associated with querying the human to learn preferences. Therefore, an effective agent ought to intelligently trade-off exploration (of the environment and human) and exploitation. We study these trade-offs theoretically and empirically in a toy bandit alignment problem which resembles the beta-Bernoulli bandit. We demonstrate while naive exploration algorithms which reflect current practices and even touted algorithms such as Thompson sampling both fail to provide acceptable solutions to this problem, information-directed sampling achieves favorable regret.

The Need for a Big World Simulator: A Scientific Challenge for Continual Learning

The "small agent, big world" frame offers a conceptual view that motivates the need for continual learning. The idea is that a small agent operating in a much bigger world cannot store all information that the world has to offer. To perform well, the agent must be carefully designed to ingest, retain, and eject the right information. To enable the development of performant continual learning agents, a number of synthetic environments have been proposed. However, these benchmarks suffer from limitations, including unnatural distribution shifts and a lack of fidelity to the "small agent, big world" framing. This paper aims to formalize two desiderata for the design of future simulated environments. These two criteria aim to reflect the objectives and complexity of continual learning in practical settings while enabling rapid prototyping of algorithms on a smaller scale.

Information-Theoretic Foundations for Machine Learning

The staggering progress of machine learning in the past decade has been a sight to behold. In retrospect, it is both remarkable and unsettling that these milestones were achievable with little to no rigorous theory to guide experimentation. Despite this fact, practitioners have been able to guide their future experimentation via observations from previous large-scale empirical investigations. However, alluding to Plato's Allegory of the cave, it is likely that the observations which form the field's notion of reality are but shadows representing fragments of that reality. In this work, we propose a theoretical framework which attempts to answer what exists outside of the cave. To the theorist, we provide a framework which is mathematically rigorous and leaves open many interesting ideas for future exploration. To the practitioner, we provide a framework whose results are very intuitive, general, and which will help form principles to guide future investigations. Concretely, we provide a theoretical framework rooted in Bayesian statistics and Shannon's information theory which is general enough to unify the analysis of many phenomena in machine learning. Our framework characterizes the performance of an optimal Bayesian learner, which considers the fundamental limits of information. Throughout this work, we derive very general theoretical results and apply them to derive insights specific to settings ranging from data which is independently and identically distributed under an unknown distribution, to data which is sequential, to data which exhibits hierarchical structure amenable to meta-learning. We conclude with a section dedicated to characterizing the performance of misspecified algorithms. These results are exciting and particularly relevant as we strive to overcome increasingly difficult machine learning challenges in this endlessly complex world.

Information-Theoretic Foundations for Neural Scaling Laws

Neural scaling laws aim to characterize how out-of-sample error behaves as a function of model and training dataset size. Such scaling laws guide allocation of a computational resources between model and data processing to minimize error. However, existing theoretical support for neural scaling laws lacks rigor and clarity, entangling the roles of information and optimization. In this work, we develop rigorous information-theoretic foundations for neural scaling laws. This allows us to characterize scaling laws for data generated by a two-layer neural network of infinite width. We observe that the optimal relation between data and model size is linear, up to logarithmic factors, corroborating large-scale empirical investigations. Concise yet general results of the kind we establish may bring clarity to this topic and inform future investigations.

Adaptive Crowdsourcing Via Self-Supervised Learning

Common crowdsourcing systems average estimates of a latent quantity of interest provided by many crowdworkers to produce a group estimate. We develop a new approach -- predict-each-worker -- that leverages self-supervised learning and a novel aggregation scheme. This approach adapts weights assigned to crowdworkers based on estimates they provided for previous quantities. When skills vary across crowdworkers or their estimates correlate, the weighted sum offers a more accurate group estimate than the average. Existing algorithms such as expectation maximization can, at least in principle, produce similarly accurate group estimates. However, their computational requirements become onerous when complex models, such as neural networks, are required to express relationships among crowdworkers. Predict-each-worker accommodates such complexity as well as many other practical challenges. We analyze the efficacy of predict-each-worker through theoretical and computational studies. Among other things, we establish asymptotic optimality as the number of engagements per crowdworker grows.

An Information-Theoretic Analysis of In-Context Learning

Previous theoretical results pertaining to meta-learning on sequences build on contrived assumptions and are somewhat convoluted. We introduce new information-theoretic tools that lead to an elegant and very general decomposition of error into three components: irreducible error, meta-learning error, and intra-task error. These tools unify analyses across many meta-learning challenges. To illustrate, we apply them to establish new results about in-context learning with transformers. Our theoretical results characterizes how error decays in both the number of training sequences and sequence lengths. Our results are very general; for example, they avoid contrived mixing time assumptions made by all prior results that establish decay of error with sequence length.

Continual Learning as Computationally Constrained Reinforcement Learning

An agent that efficiently accumulates knowledge to develop increasingly sophisticated skills over a long lifetime could advance the frontier of artificial intelligence capabilities. The design of such agents, which remains a long-standing challenge of artificial intelligence, is addressed by the subject of continual learning. This monograph clarifies and formalizes concepts of continual learning, introducing a framework and set of tools to stimulate further research.

An Information-Theoretic Analysis of Compute-Optimal Neural Scaling Laws

We study the compute-optimal trade-off between model and training data set sizes for large neural networks. Our result suggests a linear relation similar to that supported by the empirical analysis of Chinchilla. While that work studies transformer-based large language models trained on the MassiveText corpus (gopher), as a starting point for development of a mathematical theory, we focus on a simpler learning model and data generating process, each based on a neural network with a sigmoidal output unit and single hidden layer of ReLU activation units. We establish an upper bound on the minimal information-theoretically achievable expected error as a function of model and data set sizes. We then derive allocations of computation that minimize this bound. We present empirical results which suggest that this approximation correctly identifies an asymptotic linear compute-optimal scaling. This approximation can also generate new insights. Among other things, it suggests that, as the input space dimension or latent space complexity grows, as might be the case for example if a longer history of tokens is taken as input to a language model, a larger fraction of the compute budget should be allocated to growing the learning model rather than training data set.

Is Stochastic Gradient Descent Near Optimal?

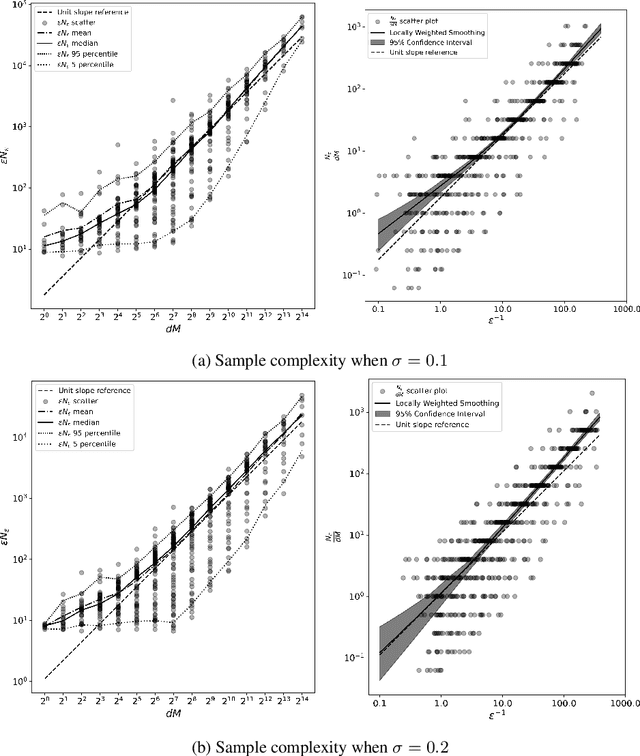
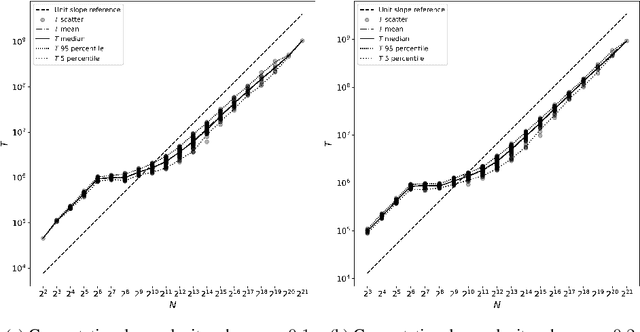
The success of neural networks over the past decade has established them as effective models for many relevant data generating processes. Statistical theory on neural networks indicates graceful scaling of sample complexity. For example, Joen & Van Roy (arXiv:2203.00246) demonstrate that, when data is generated by a ReLU teacher network with $W$ parameters, an optimal learner needs only $\tilde{O}(W/\epsilon)$ samples to attain expected error $\epsilon$. However, existing computational theory suggests that, even for single-hidden-layer teacher networks, to attain small error for all such teacher networks, the computation required to achieve this sample complexity is intractable. In this work, we fit single-hidden-layer neural networks to data generated by single-hidden-layer ReLU teacher networks with parameters drawn from a natural distribution. We demonstrate that stochastic gradient descent (SGD) with automated width selection attains small expected error with a number of samples and total number of queries both nearly linear in the input dimension and width. This suggests that SGD nearly achieves the information-theoretic sample complexity bounds of Joen & Van Roy (arXiv:2203.00246) in a computationally efficient manner. An important difference between our positive empirical results and the negative theoretical results is that the latter address worst-case error of deterministic algorithms, while our analysis centers on expected error of a stochastic algorithm.

Sample Complexity versus Depth: An Information Theoretic Analysis

Deep learning has proven effective across a range of data sets. In light of this, a natural inquiry is: "for what data generating processes can deep learning succeed?" In this work, we study the sample complexity of learning multilayer data generating processes of a sort for which deep neural networks seem to be suited. We develop general and elegant information-theoretic tools that accommodate analysis of any data generating process -- shallow or deep, parametric or nonparametric, noiseless or noisy. We then use these tools to characterize the dependence of sample complexity on the depth of multilayer processes. Our results indicate roughly linear dependence on depth. This is in contrast to previous results that suggest exponential or high-order polynomial dependence.