Is Stochastic Gradient Descent Near Optimal?
Paper and Code
Oct 06, 2022
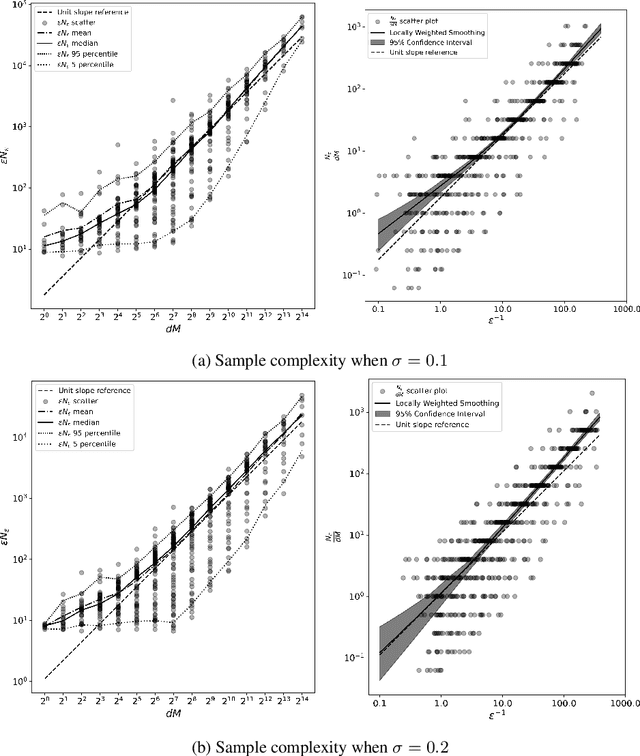

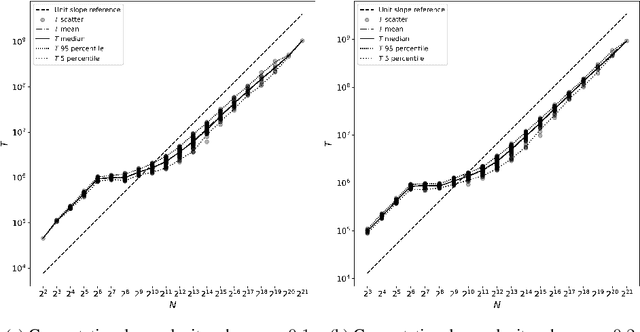
The success of neural networks over the past decade has established them as effective models for many relevant data generating processes. Statistical theory on neural networks indicates graceful scaling of sample complexity. For example, Joen & Van Roy (arXiv:2203.00246) demonstrate that, when data is generated by a ReLU teacher network with $W$ parameters, an optimal learner needs only $\tilde{O}(W/\epsilon)$ samples to attain expected error $\epsilon$. However, existing computational theory suggests that, even for single-hidden-layer teacher networks, to attain small error for all such teacher networks, the computation required to achieve this sample complexity is intractable. In this work, we fit single-hidden-layer neural networks to data generated by single-hidden-layer ReLU teacher networks with parameters drawn from a natural distribution. We demonstrate that stochastic gradient descent (SGD) with automated width selection attains small expected error with a number of samples and total number of queries both nearly linear in the input dimension and width. This suggests that SGD nearly achieves the information-theoretic sample complexity bounds of Joen & Van Roy (arXiv:2203.00246) in a computationally efficient manner. An important difference between our positive empirical results and the negative theoretical results is that the latter address worst-case error of deterministic algorithms, while our analysis centers on expected error of a stochastic algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge