Towards Learning High-Precision Least Squares Algorithms with Sequence Models

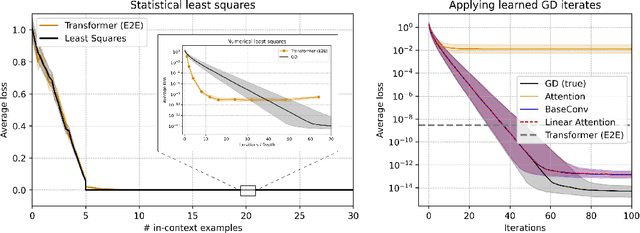
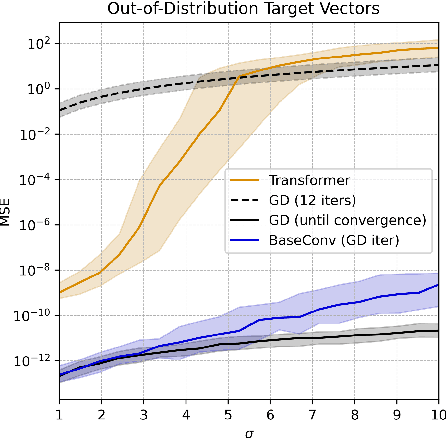
This paper investigates whether sequence models can learn to perform numerical algorithms, e.g. gradient descent, on the fundamental problem of least squares. Our goal is to inherit two properties of standard algorithms from numerical analysis: (1) machine precision, i.e. we want to obtain solutions that are accurate to near floating point error, and (2) numerical generality, i.e. we want them to apply broadly across problem instances. We find that prior approaches using Transformers fail to meet these criteria, and identify limitations present in existing architectures and training procedures. First, we show that softmax Transformers struggle to perform high-precision multiplications, which prevents them from precisely learning numerical algorithms. Second, we identify an alternate class of architectures, comprised entirely of polynomials, that can efficiently represent high-precision gradient descent iterates. Finally, we investigate precision bottlenecks during training and address them via a high-precision training recipe that reduces stochastic gradient noise. Our recipe enables us to train two polynomial architectures, gated convolutions and linear attention, to perform gradient descent iterates on least squares problems. For the first time, we demonstrate the ability to train to near machine precision. Applied iteratively, our models obtain 100,000x lower MSE than standard Transformers trained end-to-end and they incur a 10,000x smaller generalization gap on out-of-distribution problems. We make progress towards end-to-end learning of numerical algorithms for least squares.

Just read twice: closing the recall gap for recurrent language models

Recurrent large language models that compete with Transformers in language modeling perplexity are emerging at a rapid rate (e.g., Mamba, RWKV). Excitingly, these architectures use a constant amount of memory during inference. However, due to the limited memory, recurrent LMs cannot recall and use all the information in long contexts leading to brittle in-context learning (ICL) quality. A key challenge for efficient LMs is selecting what information to store versus discard. In this work, we observe the order in which information is shown to the LM impacts the selection difficulty. To formalize this, we show that the hardness of information recall reduces to the hardness of a problem called set disjointness (SD), a quintessential problem in communication complexity that requires a streaming algorithm (e.g., recurrent model) to decide whether inputted sets are disjoint. We empirically and theoretically show that the recurrent memory required to solve SD changes with set order, i.e., whether the smaller set appears first in-context. Our analysis suggests, to mitigate the reliance on data order, we can put information in the right order in-context or process prompts non-causally. Towards that end, we propose: (1) JRT-Prompt, where context gets repeated multiple times in the prompt, effectively showing the model all data orders. This gives $11.0 \pm 1.3$ points of improvement, averaged across $16$ recurrent LMs and the $6$ ICL tasks, with $11.9\times$ higher throughput than FlashAttention-2 for generation prefill (length $32$k, batch size $16$, NVidia H100). We then propose (2) JRT-RNN, which uses non-causal prefix-linear-attention to process prompts and provides $99\%$ of Transformer quality at $360$M params., $30$B tokens and $96\%$ at $1.3$B params., $50$B tokens on average across the tasks, with $19.2\times$ higher throughput for prefill than FA2.

Continual Learning as Computationally Constrained Reinforcement Learning

An agent that efficiently accumulates knowledge to develop increasingly sophisticated skills over a long lifetime could advance the frontier of artificial intelligence capabilities. The design of such agents, which remains a long-standing challenge of artificial intelligence, is addressed by the subject of continual learning. This monograph clarifies and formalizes concepts of continual learning, introducing a framework and set of tools to stimulate further research.

Gaussian Process Policy Optimization

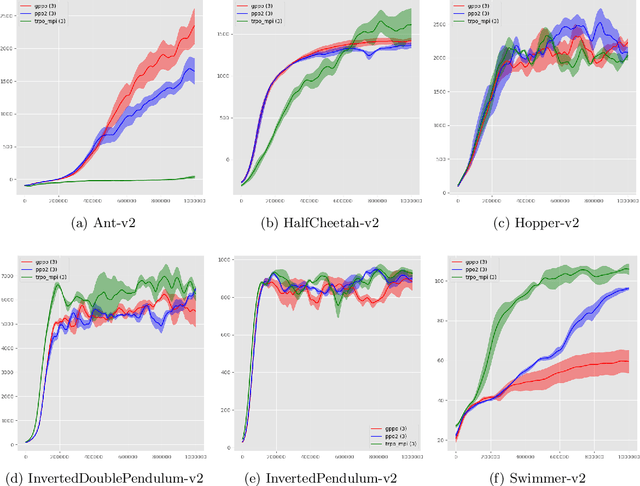
We propose a novel actor-critic, model-free reinforcement learning algorithm which employs a Bayesian method of parameter space exploration to solve environments. A Gaussian process is used to learn the expected return of a policy given the policy's parameters. The system is trained by updating the parameters using gradient descent on a new surrogate loss function consisting of the Proximal Policy Optimization 'Clipped' loss function and a bonus term representing the expected improvement acquisition function given by the Gaussian process. This new method is shown to be comparable to and at times empirically outperform current algorithms on environments that simulate robotic locomotion using the MuJoCo physics engine.