The Cell Must Go On: Agar.io for Continual Reinforcement Learning

Continual reinforcement learning (RL) concerns agents that are expected to learn continually, rather than converge to a policy that is then fixed for evaluation. Such an approach is well suited to environments the agent perceives as changing, which renders any static policy ineffective over time. The few simulators explicitly designed for empirical research in continual RL are often limited in scope or complexity, and it is now common for researchers to modify episodic RL environments by artificially incorporating abrupt task changes during interaction. In this paper, we introduce AgarCL, a research platform for continual RL that allows for a progression of increasingly sophisticated behaviour. AgarCL is based on the game Agar.io, a non-episodic, high-dimensional problem featuring stochastic, ever-evolving dynamics, continuous actions, and partial observability. Additionally, we provide benchmark results reporting the performance of DQN, PPO, and SAC in both the primary, challenging continual RL problem, and across a suite of smaller tasks within AgarCL, each of which isolates aspects of the full environment and allow us to characterize the challenges posed by different aspects of the game.

Reward-Aware Proto-Representations in Reinforcement Learning

In recent years, the successor representation (SR) has attracted increasing attention in reinforcement learning (RL), and it has been used to address some of its key challenges, such as exploration, credit assignment, and generalization. The SR can be seen as representing the underlying credit assignment structure of the environment by implicitly encoding its induced transition dynamics. However, the SR is reward-agnostic. In this paper, we discuss a similar representation that also takes into account the reward dynamics of the problem. We study the default representation (DR), a recently proposed representation with limited theoretical (and empirical) analysis. Here, we lay some of the theoretical foundation underlying the DR in the tabular case by (1) deriving dynamic programming and (2) temporal-difference methods to learn the DR, (3) characterizing the basis for the vector space of the DR, and (4) formally extending the DR to the function approximation case through default features. Empirically, we analyze the benefits of the DR in many of the settings in which the SR has been applied, including (1) reward shaping, (2) option discovery, (3) exploration, and (4) transfer learning. Our results show that, compared to the SR, the DR gives rise to qualitatively different, reward-aware behaviour and quantitatively better performance in several settings.

MaestroMotif: Skill Design from Artificial Intelligence Feedback

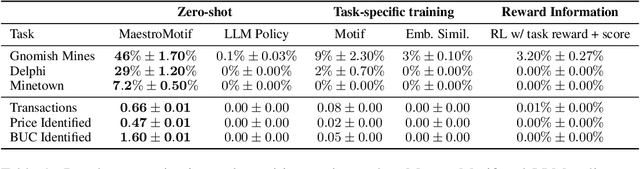
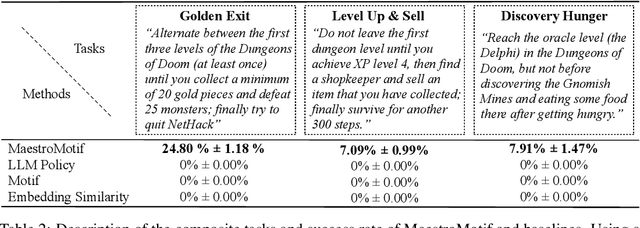
Describing skills in natural language has the potential to provide an accessible way to inject human knowledge about decision-making into an AI system. We present MaestroMotif, a method for AI-assisted skill design, which yields high-performing and adaptable agents. MaestroMotif leverages the capabilities of Large Language Models (LLMs) to effectively create and reuse skills. It first uses an LLM's feedback to automatically design rewards corresponding to each skill, starting from their natural language description. Then, it employs an LLM's code generation abilities, together with reinforcement learning, for training the skills and combining them to implement complex behaviors specified in language. We evaluate MaestroMotif using a suite of complex tasks in the NetHack Learning Environment (NLE), demonstrating that it surpasses existing approaches in both performance and usability.

Plastic Learning with Deep Fourier Features

Deep neural networks can struggle to learn continually in the face of non-stationarity. This phenomenon is known as loss of plasticity. In this paper, we identify underlying principles that lead to plastic algorithms. In particular, we provide theoretical results showing that linear function approximation, as well as a special case of deep linear networks, do not suffer from loss of plasticity. We then propose deep Fourier features, which are the concatenation of a sine and cosine in every layer, and we show that this combination provides a dynamic balance between the trainability obtained through linearity and the effectiveness obtained through the nonlinearity of neural networks. Deep networks composed entirely of deep Fourier features are highly trainable and sustain their trainability over the course of learning. Our empirical results show that continual learning performance can be drastically improved by replacing ReLU activations with deep Fourier features. These results hold for different continual learning scenarios (e.g., label noise, class incremental learning, pixel permutations) on all major supervised learning datasets used for continual learning research, such as CIFAR10, CIFAR100, and tiny-ImageNet.

Demystifying the Recency Heuristic in Temporal-Difference Learning

The recency heuristic in reinforcement learning is the assumption that stimuli that occurred closer in time to an acquired reward should be more heavily reinforced. The recency heuristic is one of the key assumptions made by TD($\lambda$), which reinforces recent experiences according to an exponentially decaying weighting. In fact, all other widely used return estimators for TD learning, such as $n$-step returns, satisfy a weaker (i.e., non-monotonic) recency heuristic. Why is the recency heuristic effective for temporal credit assignment? What happens when credit is assigned in a way that violates this heuristic? In this paper, we analyze the specific mathematical implications of adopting the recency heuristic in TD learning. We prove that any return estimator satisfying this heuristic: 1) is guaranteed to converge to the correct value function, 2) has a relatively fast contraction rate, and 3) has a long window of effective credit assignment, yet bounded worst-case variance. We also give a counterexample where on-policy, tabular TD methods violating the recency heuristic diverge. Our results offer some of the first theoretical evidence that credit assignment based on the recency heuristic facilitates learning.

Learning Continually by Spectral Regularization

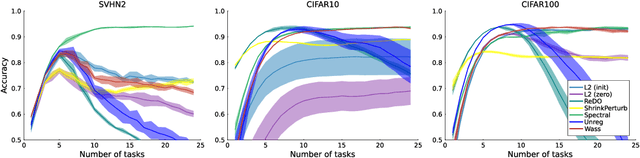
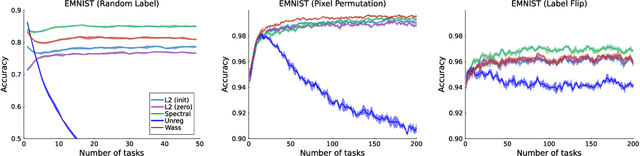
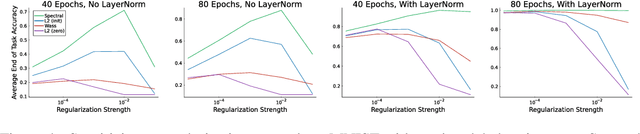
Loss of plasticity is a phenomenon where neural networks become more difficult to train during the course of learning. Continual learning algorithms seek to mitigate this effect by sustaining good predictive performance while maintaining network trainability. We develop new techniques for improving continual learning by first reconsidering how initialization can ensure trainability during early phases of learning. From this perspective, we derive new regularization strategies for continual learning that ensure beneficial initialization properties are better maintained throughout training. In particular, we investigate two new regularization techniques for continual learning: (i) Wasserstein regularization toward the initial weight distribution, which is less restrictive than regularizing toward initial weights; and (ii) regularizing weight matrix singular values, which directly ensures gradient diversity is maintained throughout training. We present an experimental analysis that shows these alternative regularizers can improve continual learning performance across a range of supervised learning tasks and model architectures. The alternative regularizers prove to be less sensitive to hyperparameters while demonstrating better training in individual tasks, sustaining trainability as new tasks arrive, and achieving better generalization performance.

Compound Returns Reduce Variance in Reinforcement Learning

Multistep returns, such as $n$-step returns and $\lambda$-returns, are commonly used to improve the sample efficiency of reinforcement learning (RL) methods. The variance of the multistep returns becomes the limiting factor in their length; looking too far into the future increases variance and reverses the benefits of multistep learning. In our work, we demonstrate the ability of compound returns -- weighted averages of $n$-step returns -- to reduce variance. We prove for the first time that any compound return with the same contraction modulus as a given $n$-step return has strictly lower variance. We additionally prove that this variance-reduction property improves the finite-sample complexity of temporal-difference learning under linear function approximation. Because general compound returns can be expensive to implement, we introduce two-bootstrap returns which reduce variance while remaining efficient, even when using minibatched experience replay. We conduct experiments showing that two-bootstrap returns can improve the sample efficiency of $n$-step deep RL agents, with little additional computational cost.

Harnessing Discrete Representations For Continual Reinforcement Learning

Reinforcement learning (RL) agents make decisions using nothing but observations from the environment, and consequently, heavily rely on the representations of those observations. Though some recent breakthroughs have used vector-based categorical representations of observations, often referred to as discrete representations, there is little work explicitly assessing the significance of such a choice. In this work, we provide a thorough empirical investigation of the advantages of representing observations as vectors of categorical values within the context of reinforcement learning. We perform evaluations on world-model learning, model-free RL, and ultimately continual RL problems, where the benefits best align with the needs of the problem setting. We find that, when compared to traditional continuous representations, world models learned over discrete representations accurately model more of the world with less capacity, and that agents trained with discrete representations learn better policies with less data. In the context of continual RL, these benefits translate into faster adapting agents. Additionally, our analysis suggests that the observed performance improvements can be attributed to the information contained within the latent vectors and potentially the encoding of the discrete representation itself.

GVFs in the Real World: Making Predictions Online for Water Treatment

In this paper we investigate the use of reinforcement-learning based prediction approaches for a real drinking-water treatment plant. Developing such a prediction system is a critical step on the path to optimizing and automating water treatment. Before that, there are many questions to answer about the predictability of the data, suitable neural network architectures, how to overcome partial observability and more. We first describe this dataset, and highlight challenges with seasonality, nonstationarity, partial observability, and heterogeneity across sensors and operation modes of the plant. We then describe General Value Function (GVF) predictions -- discounted cumulative sums of observations -- and highlight why they might be preferable to classical n-step predictions common in time series prediction. We discuss how to use offline data to appropriately pre-train our temporal difference learning (TD) agents that learn these GVF predictions, including how to select hyperparameters for online fine-tuning in deployment. We find that the TD-prediction agent obtains an overall lower normalized mean-squared error than the n-step prediction agent. Finally, we show the importance of learning in deployment, by comparing a TD agent trained purely offline with no online updating to a TD agent that learns online. This final result is one of the first to motivate the importance of adapting predictions in real-time, for non-stationary high-volume systems in the real world.

Curvature Explains Loss of Plasticity

Loss of plasticity is a phenomenon in which neural networks lose their ability to learn from new experience. Despite being empirically observed in several problem settings, little is understood about the mechanisms that lead to loss of plasticity. In this paper, we offer a consistent explanation for plasticity loss, based on an assertion that neural networks lose directions of curvature during training and that plasticity loss can be attributed to this reduction in curvature. To support such a claim, we provide a systematic empirical investigation of plasticity loss across several continual supervised learning problems. Our findings illustrate that curvature loss coincides with and sometimes precedes plasticity loss, while also showing that previous explanations are insufficient to explain loss of plasticity in all settings. Lastly, we show that regularizers which mitigate loss of plasticity also preserve curvature, motivating a simple distributional regularizer that proves to be effective across the problem settings considered.