On Centralized Critics in Multi-Agent Reinforcement Learning

Centralized Training for Decentralized Execution where agents are trained offline in a centralized fashion and execute online in a decentralized manner, has become a popular approach in Multi-Agent Reinforcement Learning (MARL). In particular, it has become popular to develop actor-critic methods that train decentralized actors with a centralized critic where the centralized critic is allowed access global information of the entire system, including the true system state. Such centralized critics are possible given offline information and are not used for online execution. While these methods perform well in a number of domains and have become a de facto standard in MARL, using a centralized critic in this context has yet to be sufficiently analyzed theoretically or empirically. In this paper, we therefore formally analyze centralized and decentralized critic approaches, and analyze the effect of using state-based critics in partially observable environments. We derive theories contrary to the common intuition: critic centralization is not strictly beneficial, and using state values can be harmful. We further prove that, in particular, state-based critics can introduce unexpected bias and variance compared to history-based critics. Finally, we demonstrate how the theory applies in practice by comparing different forms of critics on a wide range of common multi-agent benchmarks. The experiments show practical issues such as the difficulty of representation learning with partial observability, which highlights why the theoretical problems are often overlooked in the literature.

Demystifying the Recency Heuristic in Temporal-Difference Learning

The recency heuristic in reinforcement learning is the assumption that stimuli that occurred closer in time to an acquired reward should be more heavily reinforced. The recency heuristic is one of the key assumptions made by TD($\lambda$), which reinforces recent experiences according to an exponentially decaying weighting. In fact, all other widely used return estimators for TD learning, such as $n$-step returns, satisfy a weaker (i.e., non-monotonic) recency heuristic. Why is the recency heuristic effective for temporal credit assignment? What happens when credit is assigned in a way that violates this heuristic? In this paper, we analyze the specific mathematical implications of adopting the recency heuristic in TD learning. We prove that any return estimator satisfying this heuristic: 1) is guaranteed to converge to the correct value function, 2) has a relatively fast contraction rate, and 3) has a long window of effective credit assignment, yet bounded worst-case variance. We also give a counterexample where on-policy, tabular TD methods violating the recency heuristic diverge. Our results offer some of the first theoretical evidence that credit assignment based on the recency heuristic facilitates learning.

Compound Returns Reduce Variance in Reinforcement Learning

Multistep returns, such as $n$-step returns and $\lambda$-returns, are commonly used to improve the sample efficiency of reinforcement learning (RL) methods. The variance of the multistep returns becomes the limiting factor in their length; looking too far into the future increases variance and reverses the benefits of multistep learning. In our work, we demonstrate the ability of compound returns -- weighted averages of $n$-step returns -- to reduce variance. We prove for the first time that any compound return with the same contraction modulus as a given $n$-step return has strictly lower variance. We additionally prove that this variance-reduction property improves the finite-sample complexity of temporal-difference learning under linear function approximation. Because general compound returns can be expensive to implement, we introduce two-bootstrap returns which reduce variance while remaining efficient, even when using minibatched experience replay. We conduct experiments showing that two-bootstrap returns can improve the sample efficiency of $n$-step deep RL agents, with little additional computational cost.

Trajectory-Aware Eligibility Traces for Off-Policy Reinforcement Learning

Off-policy learning from multistep returns is crucial for sample-efficient reinforcement learning, but counteracting off-policy bias without exacerbating variance is challenging. Classically, off-policy bias is corrected in a per-decision manner: past temporal-difference errors are re-weighted by the instantaneous Importance Sampling (IS) ratio after each action via eligibility traces. Many off-policy algorithms rely on this mechanism, along with differing protocols for cutting the IS ratios to combat the variance of the IS estimator. Unfortunately, once a trace has been fully cut, the effect cannot be reversed. This has led to the development of credit-assignment strategies that account for multiple past experiences at a time. These trajectory-aware methods have not been extensively analyzed, and their theoretical justification remains uncertain. In this paper, we propose a multistep operator that can express both per-decision and trajectory-aware methods. We prove convergence conditions for our operator in the tabular setting, establishing the first guarantees for several existing methods as well as many new ones. Finally, we introduce Recency-Bounded Importance Sampling (RBIS), which leverages trajectory awareness to perform robustly across $\lambda$-values in an off-policy control task.

Adaptive Tree Backup Algorithms for Temporal-Difference Reinforcement Learning

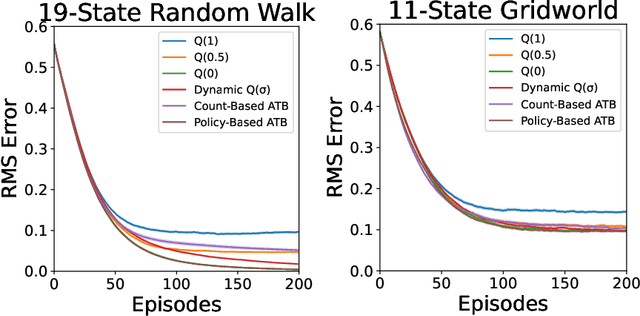
Q($\sigma$) is a recently proposed temporal-difference learning method that interpolates between learning from expected backups and sampled backups. It has been shown that intermediate values for the interpolation parameter $\sigma \in [0,1]$ perform better in practice, and therefore it is commonly believed that $\sigma$ functions as a bias-variance trade-off parameter to achieve these improvements. In our work, we disprove this notion, showing that the choice of $\sigma=0$ minimizes variance without increasing bias. This indicates that $\sigma$ must have some other effect on learning that is not fully understood. As an alternative, we hypothesize the existence of a new trade-off: larger $\sigma$-values help overcome poor initializations of the value function, at the expense of higher statistical variance. To automatically balance these considerations, we propose Adaptive Tree Backup (ATB) methods, whose weighted backups evolve as the agent gains experience. Our experiments demonstrate that adaptive strategies can be more effective than relying on fixed or time-annealed $\sigma$-values.

Improving the Efficiency of Off-Policy Reinforcement Learning by Accounting for Past Decisions

Off-policy learning from multistep returns is crucial for sample-efficient reinforcement learning, particularly in the experience replay setting now commonly used with deep neural networks. Classically, off-policy estimation bias is corrected in a per-decision manner: past temporal-difference errors are re-weighted by the instantaneous Importance Sampling (IS) ratio (via eligibility traces) after each action. Many important off-policy algorithms such as Tree Backup and Retrace rely on this mechanism along with differing protocols for truncating ("cutting") the ratios ("traces") to counteract the excessive variance of the IS estimator. Unfortunately, cutting traces on a per-decision basis is not necessarily efficient; once a trace has been cut according to local information, the effect cannot be reversed later, potentially resulting in the premature truncation of estimated returns and slower learning. In the interest of motivating efficient off-policy algorithms, we propose a multistep operator that permits arbitrary past-dependent traces. We prove that our operator is convergent for policy evaluation, and for optimal control when targeting greedy-in-the-limit policies. Our theorems establish the first convergence guarantees for many existing algorithms including Truncated IS, Non-Markov Retrace, and history-dependent TD($\lambda$). Our theoretical results also provide guidance for the development of new algorithms that jointly consider multiple past decisions for better credit assignment and faster learning.

Virtual Replay Cache

Return caching is a recent strategy that enables efficient minibatch training with multistep estimators (e.g. the {\lambda}-return) for deep reinforcement learning. By precomputing return estimates in sequential batches and then storing the results in an auxiliary data structure for later sampling, the average computation spent per estimate can be greatly reduced. Still, the efficiency of return caching could be improved, particularly with regard to its large memory usage and repetitive data copies. We propose a new data structure, the Virtual Replay Cache (VRC), to address these shortcomings. When learning to play Atari 2600 games, the VRC nearly eliminates DQN({\lambda})'s cache memory footprint and slightly reduces the total training time on our hardware.

Human-Level Control without Server-Grade Hardware

Deep Q-Network (DQN) marked a major milestone for reinforcement learning, demonstrating for the first time that human-level control policies could be learned directly from raw visual inputs via reward maximization. Even years after its introduction, DQN remains highly relevant to the research community since many of its innovations have been adopted by successor methods. Nevertheless, despite significant hardware advances in the interim, DQN's original Atari 2600 experiments remain costly to replicate in full. This poses an immense barrier to researchers who cannot afford state-of-the-art hardware or lack access to large-scale cloud computing resources. To facilitate improved access to deep reinforcement learning research, we introduce a DQN implementation that leverages a novel concurrent and synchronized execution framework designed to maximally utilize a heterogeneous CPU-GPU desktop system. With just one NVIDIA GeForce GTX 1080 GPU, our implementation reduces the training time of a 200-million-frame Atari experiment from 25 hours to just 9 hours. The ideas introduced in our paper should be generalizable to a large number of off-policy deep reinforcement learning methods.

Investigating Alternatives to the Root Mean Square for Adaptive Gradient Methods

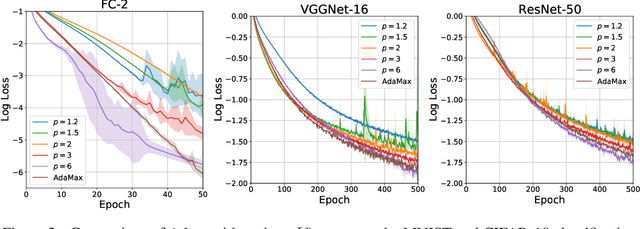
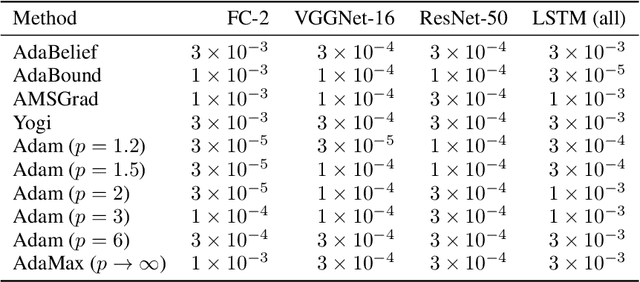
Adam is an adaptive gradient method that has experienced widespread adoption due to its fast and reliable training performance. Recent approaches have not offered significant improvement over Adam, often because they do not innovate upon one of its core features: normalization by the root mean square (RMS) of recent gradients. However, as noted by Kingma and Ba (2015), any number of $L^p$ normalizations are possible, with the RMS corresponding to the specific case of $p=2$. In our work, we theoretically and empirically characterize the influence of different $L^p$ norms on adaptive gradient methods for the first time. We show mathematically how the choice of $p$ influences the size of the steps taken, while leaving other desirable properties unaffected. We evaluate Adam with various $L^p$ norms on a suite of deep learning benchmarks, and find that $p > 2$ consistently leads to improved learning speed and final performance. The choices of $p=3$ or $p=6$ also match or outperform state-of-the-art methods in all of our experiments.

Stratified Experience Replay: Correcting Multiplicity Bias in Off-Policy Reinforcement Learning

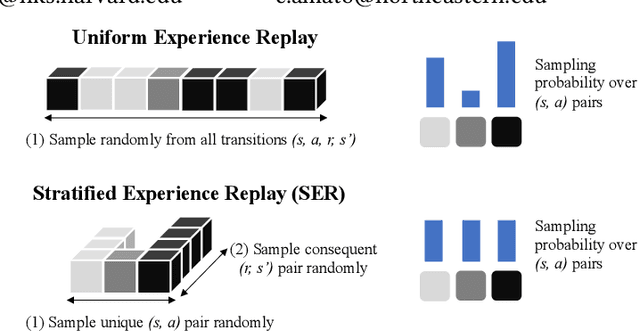
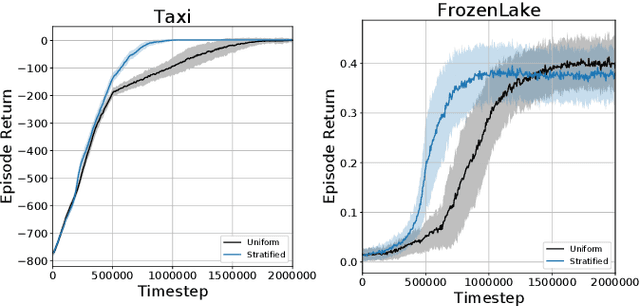
Deep Reinforcement Learning (RL) methods rely on experience replay to approximate the minibatched supervised learning setting; however, unlike supervised learning where access to lots of training data is crucial to generalization, replay-based deep RL appears to struggle in the presence of extraneous data. Recent works have shown that the performance of Deep Q-Network (DQN) degrades when its replay memory becomes too large. This suggests that outdated experiences somehow impact the performance of deep RL, which should not be the case for off-policy methods like DQN. Consequently, we re-examine the motivation for sampling uniformly over a replay memory, and find that it may be flawed when using function approximation. We show that -- despite conventional wisdom -- sampling from the uniform distribution does not yield uncorrelated training samples and therefore biases gradients during training. Our theory prescribes a special non-uniform distribution to cancel this effect, and we propose a stratified sampling scheme to efficiently implement it.