Adaptive Tree Backup Algorithms for Temporal-Difference Reinforcement Learning
Paper and Code
Jun 04, 2022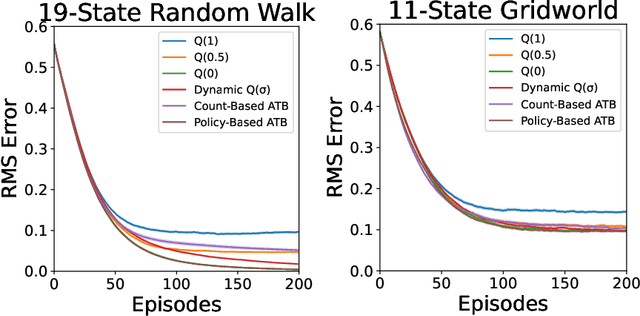
Q($\sigma$) is a recently proposed temporal-difference learning method that interpolates between learning from expected backups and sampled backups. It has been shown that intermediate values for the interpolation parameter $\sigma \in [0,1]$ perform better in practice, and therefore it is commonly believed that $\sigma$ functions as a bias-variance trade-off parameter to achieve these improvements. In our work, we disprove this notion, showing that the choice of $\sigma=0$ minimizes variance without increasing bias. This indicates that $\sigma$ must have some other effect on learning that is not fully understood. As an alternative, we hypothesize the existence of a new trade-off: larger $\sigma$-values help overcome poor initializations of the value function, at the expense of higher statistical variance. To automatically balance these considerations, we propose Adaptive Tree Backup (ATB) methods, whose weighted backups evolve as the agent gains experience. Our experiments demonstrate that adaptive strategies can be more effective than relying on fixed or time-annealed $\sigma$-values.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge