Distribution oblivious, risk-aware algorithms for multi-armed bandits with unbounded rewards
Paper and Code
Jun 03, 2019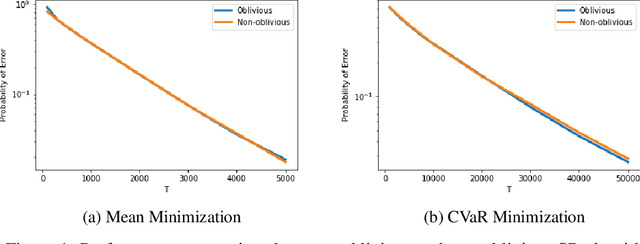
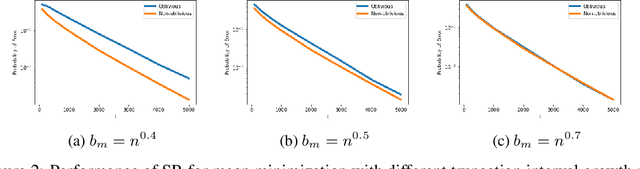
Classical multi-armed bandit problems use the expected value of an arm as a metric to evaluate its goodness. However, the expected value is a risk-neutral metric. In many applications like finance, one is interested in balancing the expected return of an arm (or portfolio) with the risk associated with that return. In this paper, we consider the problem of selecting the arm that optimizes a linear combination of the expected reward and the associated Conditional Value at Risk (CVaR) in a fixed budget best-arm identification framework. We allow the reward distributions to be unbounded or even heavy-tailed. For this problem, our goal is to devise algorithms that are entirely distribution oblivious, i.e., the algorithm is not aware of any information on the reward distributions, including bounds on the moments/tails, or the suboptimality gaps across arms. In this paper, we provide a class of such algorithms with provable upper bounds on the probability of incorrect identification. In the process, we develop a novel estimator for the CVaR of unbounded (including heavy-tailed) random variables and prove a concentration inequality for the same, which could be of independent interest. We also compare the error bounds for our distribution oblivious algorithms with those corresponding to standard non-oblivious algorithms. Finally, numerical experiments reveal that our algorithms perform competitively when compared with non-oblivious algorithms, suggesting that distribution obliviousness can be realised in practice without incurring a significant loss of performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge