Classical Bandit Algorithms for Entanglement Detection in Parameterized Qubit States

Entanglement is a key resource for a wide range of tasks in quantum information and computing. Thus, verifying availability of this quantum resource is essential. Extensive research on entanglement detection has led to no-go theorems (Lu et al. [Phys. Rev. Lett., 116, 230501 (2016)]) that highlight the need for full state tomography (FST) in the absence of adaptive or joint measurements. Recent advancements, as proposed by Zhu, Teo, and Englert [Phys. Rev. A, 81, 052339, 2010], introduce a single-parameter family of entanglement witness measurements which are capable of conclusively detecting certain entangled states and only resort to FST when all witness measurements are inconclusive. We find a variety of realistic noisy two-qubit quantum states $\mathcal{F}$ that yield conclusive results under this witness family. We solve the problem of detecting entanglement among $K$ quantum states in $\mathcal{F}$, of which $m$ states are entangled, with $m$ potentially unknown. We recognize a structural connection of this problem to the Bad Arm Identification problem in stochastic Multi-Armed Bandits (MAB). In contrast to existing quantum bandit frameworks, we establish a new correspondence tailored for entanglement detection and term it the $(m,K)$-quantum Multi-Armed Bandit. We implement two well-known MAB policies for arbitrary states derived from $\mathcal{F}$, present theoretical guarantees on the measurement/sample complexity and demonstrate the practicality of the policies through numerical simulations. More broadly, this paper highlights the potential for employing classical machine learning techniques for quantum entanglement detection.

Concentration Bounds for Optimized Certainty Equivalent Risk Estimation

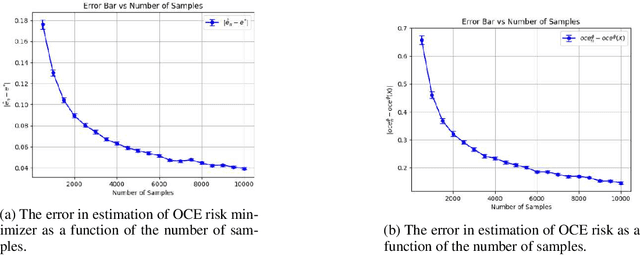
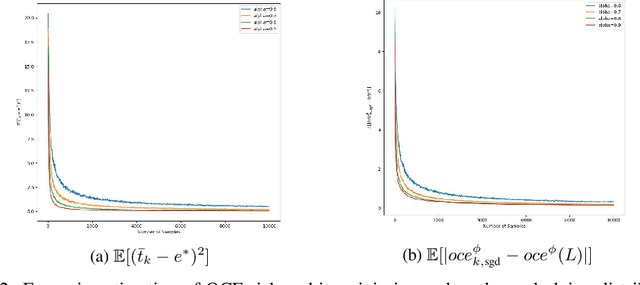
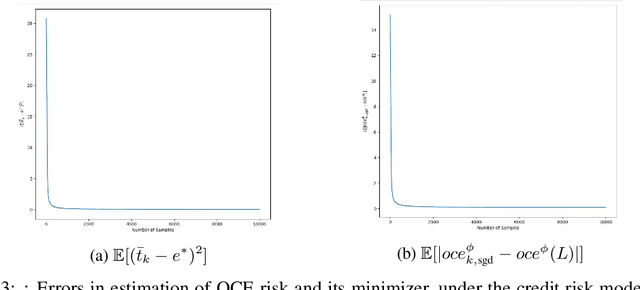
We consider the problem of estimating the Optimized Certainty Equivalent (OCE) risk from independent and identically distributed (i.i.d.) samples. For the classic sample average approximation (SAA) of OCE, we derive mean-squared error as well as concentration bounds (assuming sub-Gaussianity). Further, we analyze an efficient stochastic approximation-based OCE estimator, and derive finite sample bounds for the same. To show the applicability of our bounds, we consider a risk-aware bandit problem, with OCE as the risk. For this problem, we derive bound on the probability of mis-identification. Finally, we conduct numerical experiments to validate the theoretical findings.

A Survey of Risk-Aware Multi-Armed Bandits

In several applications such as clinical trials and financial portfolio optimization, the expected value (or the average reward) does not satisfactorily capture the merits of a drug or a portfolio. In such applications, risk plays a crucial role, and a risk-aware performance measure is preferable, so as to capture losses in the case of adverse events. This survey aims to consolidate and summarise the existing research on risk measures, specifically in the context of multi-armed bandits. We review various risk measures of interest, and comment on their properties. Next, we review existing concentration inequalities for various risk measures. Then, we proceed to defining risk-aware bandit problems, We consider algorithms for the regret minimization setting, where the exploration-exploitation trade-off manifests, as well as the best-arm identification setting, which is a pure exploration problem -- both in the context of risk-sensitive measures. We conclude by commenting on persisting challenges and fertile areas for future research.

Online Estimation and Optimization of Utility-Based Shortfall Risk

Utility-Based Shortfall Risk (UBSR) is a risk metric that is increasingly popular in financial applications, owing to certain desirable properties that it enjoys. We consider the problem of estimating UBSR in a recursive setting, where samples from the underlying loss distribution are available one-at-a-time. We cast the UBSR estimation problem as a root finding problem, and propose stochastic approximation-based estimations schemes. We derive non-asymptotic bounds on the estimation error in the number of samples. We also consider the problem of UBSR optimization within a parameterized class of random variables. We propose a stochastic gradient descent based algorithm for UBSR optimization, and derive non-asymptotic bounds on its convergence.

Statistically Robust, Risk-Averse Best Arm Identification in Multi-Armed Bandits

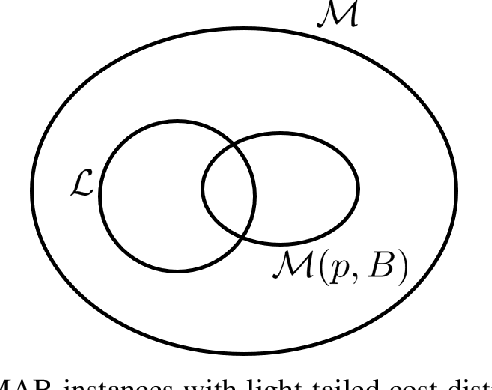
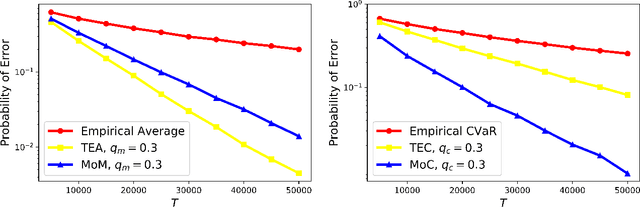
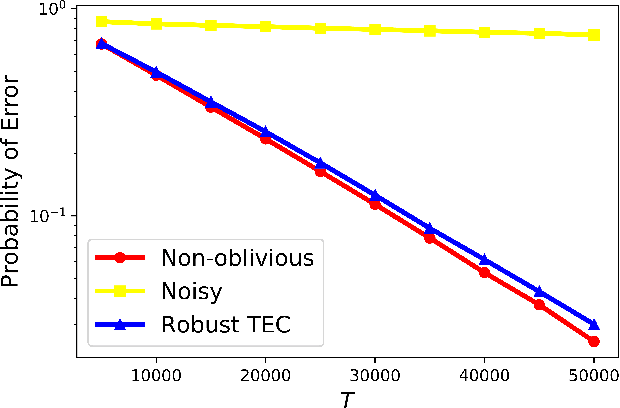
Traditional multi-armed bandit (MAB) formulations usually make certain assumptions about the underlying arms' distributions, such as bounds on the support or their tail behaviour. Moreover, such parametric information is usually 'baked' into the algorithms. In this paper, we show that specialized algorithms that exploit such parametric information are prone to inconsistent learning performance when the parameter is misspecified. Our key contributions are twofold: (i) We establish fundamental performance limits of statistically robust MAB algorithms under the fixed-budget pure exploration setting, and (ii) We propose two classes of algorithms that are asymptotically near-optimal. Additionally, we consider a risk-aware criterion for best arm identification, where the objective associated with each arm is a linear combination of the mean and the conditional value at risk (CVaR). Throughout, we make a very mild 'bounded moment' assumption, which lets us work with both light-tailed and heavy-tailed distributions within a unified framework.

Bandit algorithms: Letting go of logarithmic regret for statistical robustness

We study regret minimization in a stochastic multi-armed bandit setting and establish a fundamental trade-off between the regret suffered under an algorithm, and its statistical robustness. Considering broad classes of underlying arms' distributions, we show that bandit learning algorithms with logarithmic regret are always inconsistent and that consistent learning algorithms always suffer a super-logarithmic regret. This result highlights the inevitable statistical fragility of all `logarithmic regret' bandit algorithms available in the literature---for instance, if a UCB algorithm designed for $\sigma$-subGaussian distributions is used in a subGaussian setting with a mismatched variance parameter, the learning performance could be inconsistent. Next, we show a positive result: statistically robust and consistent learning performance is attainable if we allow the regret to be slightly worse than logarithmic. Specifically, we propose three classes of distribution oblivious algorithms that achieve an asymptotic regret that is arbitrarily close to logarithmic.

Constrained regret minimization for multi-criterion multi-armed bandits

We consider a stochastic multi-armed bandit setting and study the problem of regret minimization over a given time horizon, subject to a risk constraint. Each arm is associated with an unknown cost/loss distribution. The learning agent is characterized by a risk-appetite that she is willing to tolerate, which we model using a pre-specified upper bound on the Conditional Value at Risk (CVaR). An optimal arm is one that minimizes the expected loss, among those arms that satisfy the CVaR constraint. The agent is interested in minimizing the number of pulls of suboptimal arms, including the ones that are 'too risky.' For this problem, we propose a Risk-Constrained Lower Confidence Bound (RC-LCB) algorithm, that guarantees logarithmic regret, i.e., the average number of plays of all non-optimal arms is at most logarithmic in the horizon. The algorithm also outputs a boolean flag that correctly identifies with high probability, whether the given instance was feasible/infeasible with respect to the risk constraint. We prove lower bounds on the performance of any risk-constrained regret minimization algorithm and establish a fundamental trade-off between regret minimization and feasibility identification. The proposed algorithm and analyses can be readily generalized to solve constrained multi-criterion optimization problems in the bandits setting.

A Framework for End-to-End Deep Learning-Based Anomaly Detection in Transportation Networks

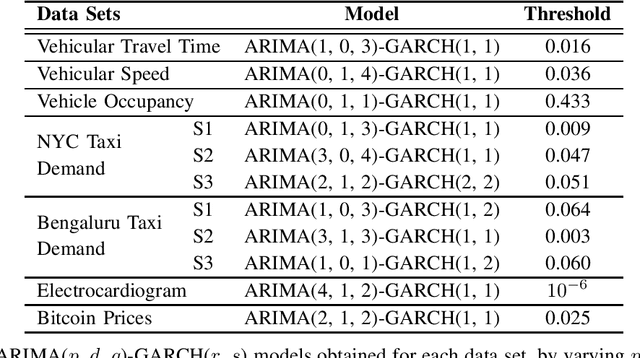
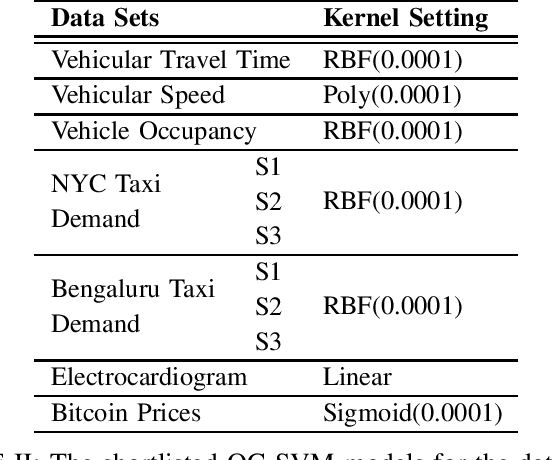
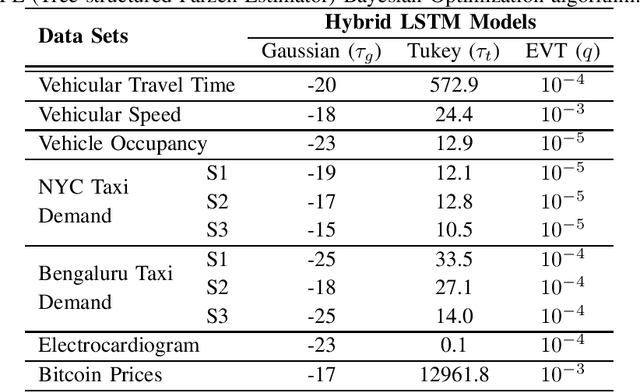
We develop an end-to-end deep learning-based anomaly detection model for temporal data in transportation networks. The proposed EVT-LSTM model is derived from the popular LSTM (Long Short-Term Memory) network and adopts an objective function that is based on fundamental results from EVT (Extreme Value Theory). We compare the EVT-LSTM model with some established statistical, machine learning, and hybrid deep learning baselines. Experiments on seven diverse real-world data sets demonstrate the superior anomaly detection performance of our proposed model over the other models considered in the comparison study.

LSTM-Based Anomaly Detection: Detection Rules from Extreme Value Theory

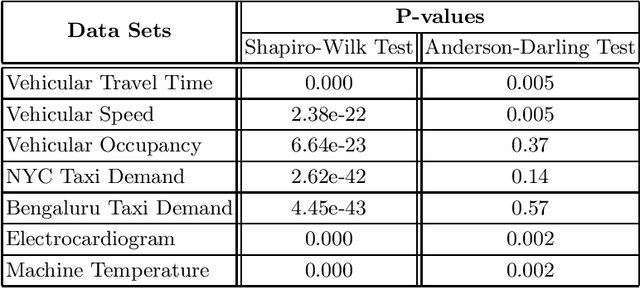
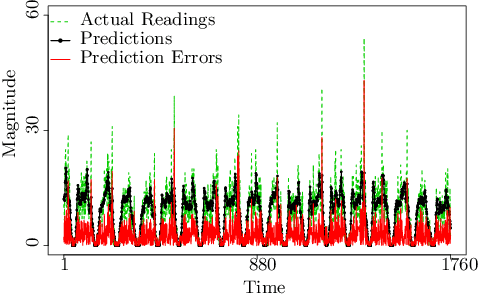
In this paper, we explore various statistical techniques for anomaly detection in conjunction with the popular Long Short-Term Memory (LSTM) deep learning model for transportation networks. We obtain the prediction errors from an LSTM model, and then apply three statistical models based on (i) the Gaussian distribution, (ii) Extreme Value Theory (EVT), and (iii) the Tukey's method. Using statistical tests and numerical studies, we find strong evidence against the widely employed Gaussian distribution based detection rule on the prediction errors. Next, motivated by fundamental results from Extreme Value Theory, we propose a detection technique that does not assume any parent distribution on the prediction errors. Through numerical experiments conducted on several real-world traffic data sets, we show that the EVT-based detection rule is superior to other detection rules, and is supported by statistical evidence.

Distribution oblivious, risk-aware algorithms for multi-armed bandits with unbounded rewards

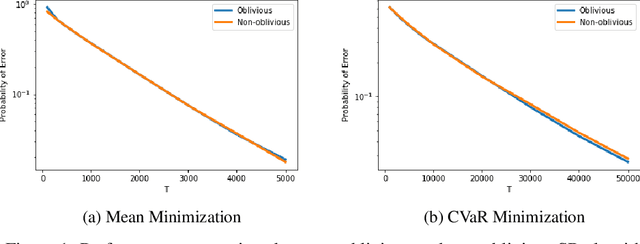
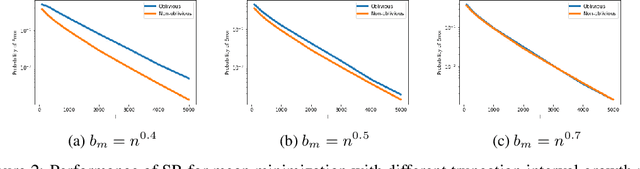
Classical multi-armed bandit problems use the expected value of an arm as a metric to evaluate its goodness. However, the expected value is a risk-neutral metric. In many applications like finance, one is interested in balancing the expected return of an arm (or portfolio) with the risk associated with that return. In this paper, we consider the problem of selecting the arm that optimizes a linear combination of the expected reward and the associated Conditional Value at Risk (CVaR) in a fixed budget best-arm identification framework. We allow the reward distributions to be unbounded or even heavy-tailed. For this problem, our goal is to devise algorithms that are entirely distribution oblivious, i.e., the algorithm is not aware of any information on the reward distributions, including bounds on the moments/tails, or the suboptimality gaps across arms. In this paper, we provide a class of such algorithms with provable upper bounds on the probability of incorrect identification. In the process, we develop a novel estimator for the CVaR of unbounded (including heavy-tailed) random variables and prove a concentration inequality for the same, which could be of independent interest. We also compare the error bounds for our distribution oblivious algorithms with those corresponding to standard non-oblivious algorithms. Finally, numerical experiments reveal that our algorithms perform competitively when compared with non-oblivious algorithms, suggesting that distribution obliviousness can be realised in practice without incurring a significant loss of performance.