Concentration Bounds for Optimized Certainty Equivalent Risk Estimation
Paper and Code
May 31, 2024
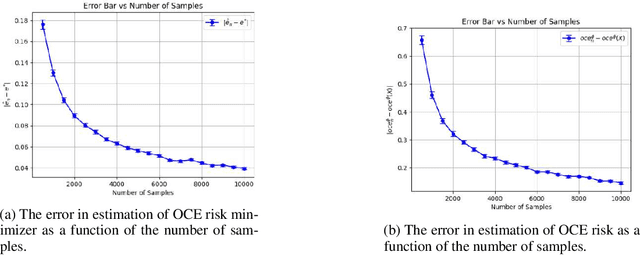
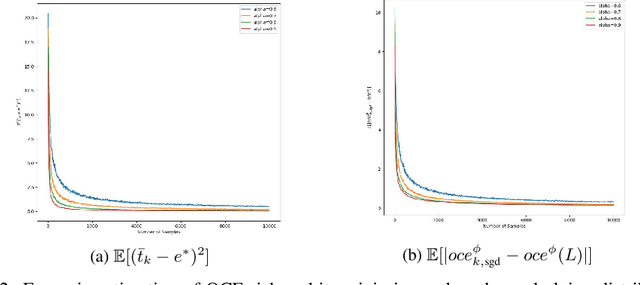
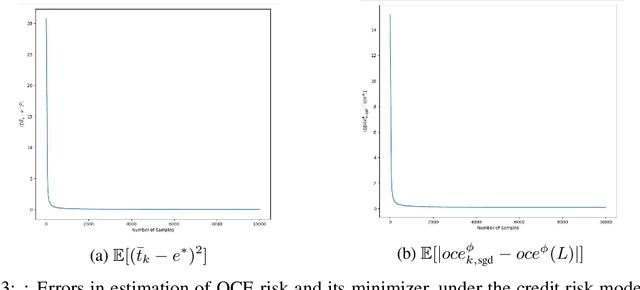
We consider the problem of estimating the Optimized Certainty Equivalent (OCE) risk from independent and identically distributed (i.i.d.) samples. For the classic sample average approximation (SAA) of OCE, we derive mean-squared error as well as concentration bounds (assuming sub-Gaussianity). Further, we analyze an efficient stochastic approximation-based OCE estimator, and derive finite sample bounds for the same. To show the applicability of our bounds, we consider a risk-aware bandit problem, with OCE as the risk. For this problem, we derive bound on the probability of mis-identification. Finally, we conduct numerical experiments to validate the theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge